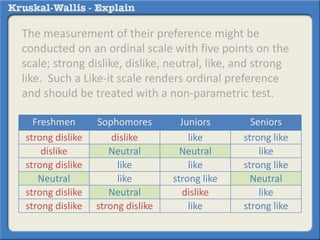
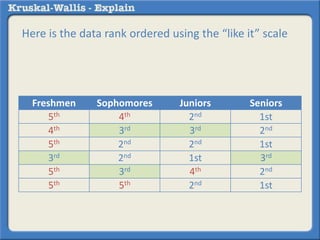
The Kruskal-Wallis test is a non-parametric analogue to a one-way ANOVA test used to compare differences between two or more independent groups when the dependent variable is measured on an ordinal scale or when the distribution is skewed. It works by ranking the data and estimating differences in ranks among the groups. For example, it could be used to test for differences in student preference for watching rugby (measured on a scale from strong dislike to strong like) between freshmen, sophomores, juniors, and seniors. A significant Kruskal-Wallis result should then be followed up with post-hoc non-parametric tests to determine where the differences between groups occur.

1. Kruskal-Wallis Test

2. The non-parametric analogue for a one-way ANOVA
test is the Kruskal-Wallis test.

3. The non-parametric analogue for a one-way ANOVA
test is the Kruskal-Wallis test.
Remember that a non-parametric test is used when
the distribution is either highly skewed or we are
comparing ordinal or rank ordered data.

4. Example of a skewed distribution
1 2 3 4 5 6

5. Example of rank ordered data
Football Players Basketball Players
1st
2nd
3rd
4th
5th
6th
7th
8th
9th
10th
Rank ordered-comparison
of
amount of pizza
slices eaten in one
sitting

6. Similar to the Mann-Whitney U test, the Kruskal-Wallis
test evaluates the differences among groups by
estimating differences in ranks among them.

7. Similar to the Mann-Whitney U test, the Kruskal-Wallis
test evaluates the differences among groups by
estimating differences in ranks among them.
For example, four groups of students, freshman,
sophomores, juniors, and seniors might be tested for
their preference to watch rugby.

8. The measurement of their preference might be
conducted on an ordinal scale with five points on the
scale; strong dislike, dislike, neutral, like, and strong
like. Such a Like-it scale renders ordinal preference
and should be treated with a non-parametric test.

9. The measurement of their preference might be
conducted on an ordinal scale with five points on the
scale; strong dislike, dislike, neutral, like, and strong
like. Such a Like-it scale renders ordinal preference
and should be treated with a non-parametric test.
Freshmen Sophomores Juniors Seniors
strong dislike dislike like strong like
dislike Neutral Neutral like
strong dislike like like strong like
Neutral like strong like Neutral
strong dislike Neutral dislike like
strong dislike strong dislike like strong like

10. Here is the data rank ordered using the “like it” scale
Freshmen Sophomores Juniors Seniors
5th 4th 2nd 1st
4th 3rd 3rd 2nd
5th 2nd 2nd 1st
3rd 2nd 1st 3rd
5th 3rd 4th 2nd
5th 5th 2nd 1st

11. As with ANOVA, here we are determining how more
than two levels (Freshmen, Sophomores, Juniors, and
Seniors) of the independent variable (year in school)
compare in terms of the dependent variable (their
preference for rugby).
preference for
Freshman
Sophomore
Junior
Senior

12. Similar to one-way ANOVA, a significant Kruskal-Wallis
result should be followed up with post-hoc tests (also
non-parametric) to determine where the differences
between groups are occurring.
preference for
Freshman
Sophomore
Junior
Senior