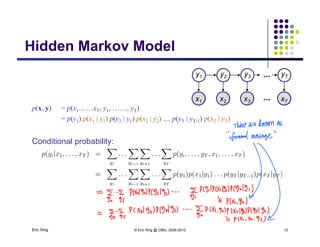
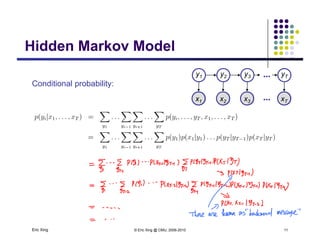
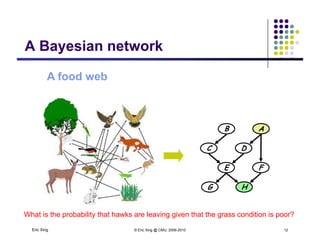
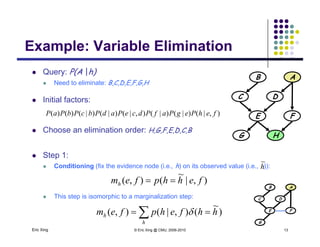
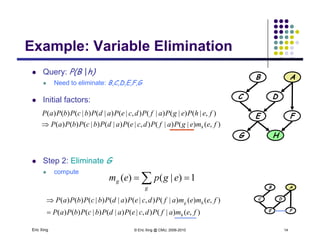
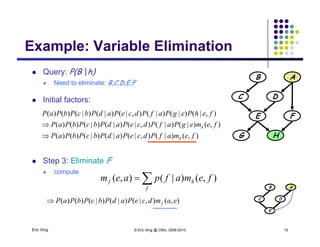
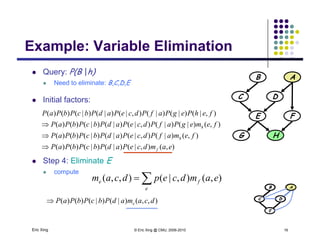
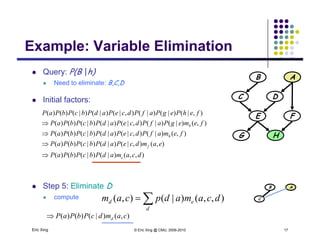
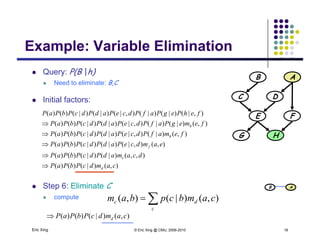
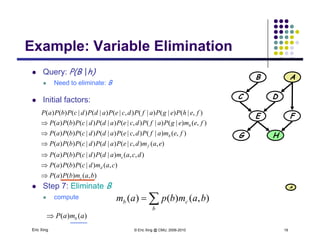
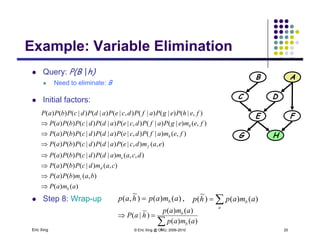
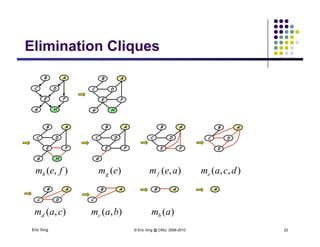
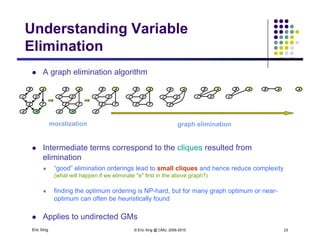
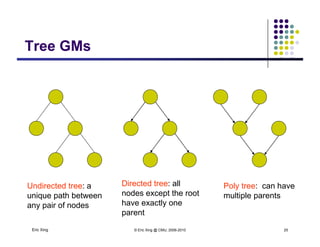
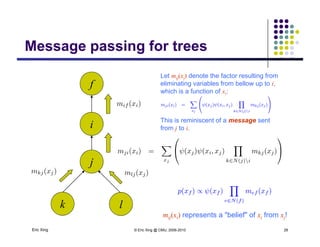
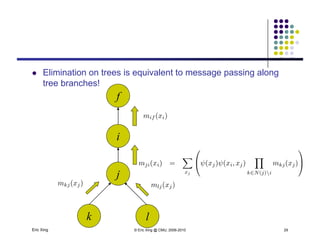
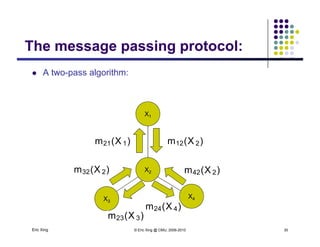
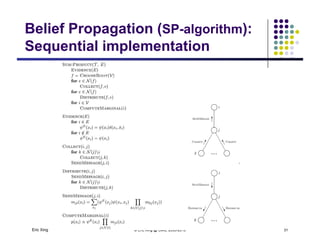
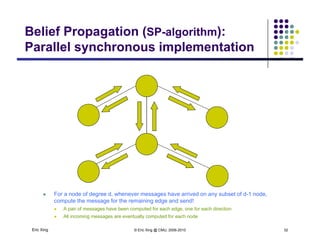
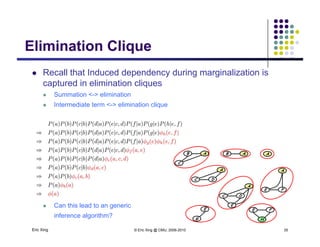
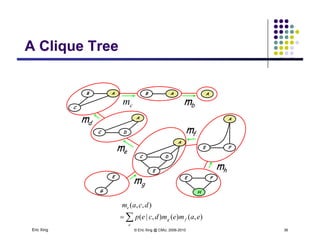
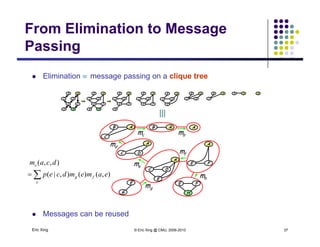
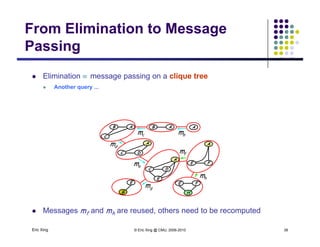
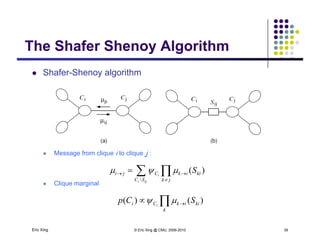
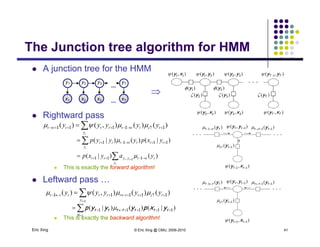
The document discusses probabilistic inference on Bayesian networks. It provides examples of common inference queries such as computing the likelihood of evidence, conditional probabilities given evidence, and the most probable assignment. It also describes the variable elimination algorithm for exact inference on general Bayesian networks through iteratively eliminating variables based on a specified elimination order. An example application of the variable elimination algorithm is shown to compute the conditional probability P(B|h) on a sample Bayesian network.