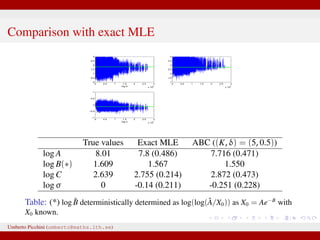
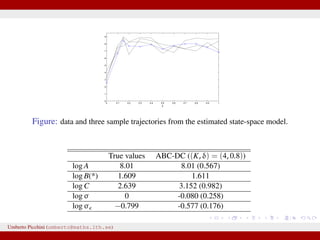
The document discusses maximum likelihood estimation of state-space stochastic differential equation (SDE) models using approximate Bayesian computation (ABC) to handle intractable likelihoods. It focuses on the use of data-cloning methods to improve estimation accuracy by increasing the effective sample size through replicating data. The combination of ABC and data cloning aims to achieve better posterior distribution estimates when traditional methods struggle with low acceptance rates.

1. Maximum likelihood estimation of state-space
SDE models using data-cloning approximate
Bayesian computation
Umberto Picchini
Centre for Mathematical Sciences,
Lund University
AMS-EMS-SPM 2015, Porto
Umberto Picchini (umberto@maths.lth.se)

2. Nowadays there are several ways to deal with “intractable
likelihoods”, that is models for which an explicit likelihood function
is unavailable.
“Plug-and-play methods”: the only requirements is the ability to
simulate from the data-generating-model.
particle marginal methods (PMMH, PMCMC) based on SMC
filters [Andrieu et al. 2010].
Iterated filtering [Ionides et al. 2011]
approximate Bayesian computation (ABC) [Marin et al. 2012].
In the following I will focus on ABC methods.
Andrieu, Doucet and Holenstein 2010. Particle Markov chain Monte Carlo methods.
JRSS-B.
Ionides, Bhadra, Atchade and King 2011. Iterated filtering. Ann. Stat.
Marin, Pudlo, Robert and Ryder 2012. Approximate Bayesian computational methods.
Stat. Comput.
Umberto Picchini (umberto@maths.lth.se)

3. A state-space model (SSM)
Yt ∼ f(yt|Xt, φ), t t0
Xt ∼ g(xt|xt−1, η).
(1)
We have data y = (y0, y1, ..., yn) from (1) at discrete time-points
0 t0 < ... < tn.
Transition densities g(xt|xt−1, η) are typically unknown.
We are interested in inference for the vector parameter θ = (φ, η),
however the likelihood function is intractable
p(y|θ) =
T
t=1
p(yt|xt; θ)p(x1)
T
t=2
p(xt|xt−1; θ)
unavailable
dx1:T
Umberto Picchini (umberto@maths.lth.se)

4. Approximate Bayesian computation (ABC)
Consider the posterior distribution of θ:
π(θ|y) ∝ p(y|θ)π(θ)
Purpose of ABC is to obtain an approximation πδ(θ|y) to the true
posterior π(θ|y).
Here δ > 0 is a tolerance value. The smaller δ the better the
approximation to π(θ|y).
In practice inference is carried via some Monte Carlo sampling from
πδ(θ|y).
However for a “small” δ sampling from πδ(θ|y) can be difficult (high
rejection rates).
Umberto Picchini (umberto@maths.lth.se)

5. ABC gives a way to approximate a posterior distribution
π(θ|y) ∝ p(y|θ)π(θ)
key to the success of ABC is the ability to bypass the explicit
calculation of the likelihood p(y|θ)
...only forward-simulation from the model is required!
Simulate artificial-data y∗ from the SSM model (1):
y∗
∼ p(y|θ)
for SDEs, use numerical discretization (arbitrarily accurate as the
stepsize h → 0) or exact simulation (see
Beskos,Roberts,Fearnhead,Papaspiliopulos).
ABC had an incredible success in genetic studies since mid 90’s
(Tavare et al ’97, Pritchard et al. ’99). Now is everywhere.
Umberto Picchini (umberto@maths.lth.se)

6. ABC basics
Generate θ∗ ∼ π(θ), x∗
t ∼ p(X|θ∗), y∗ ∼ f(yt|x∗
t , θ∗).
proposal θ∗ is accepted if y∗ is “close” to data y, according to a
threshold δ > 0.
The above generate draws from the augmented approximated
posterior
πδ(θ, y∗
|y) ∝ Jδ(y, y∗
; θ) p(y∗
|θ)π(θ)
∝π(θ|y∗)
Jδ(·) weights the intractable posterior π(θ|y∗) ∝ p(y∗|θ)π(θ) with
high values when y∗ ≈ y.
Rationale: if Jδ(·) constant when δ = 0 (y = y∗) recover the exact
posterior π(θ|y).
Example: Jδ(y, y∗; θ) ∝ n
i=1
1
δe−
y∗
i −yi
2
2δ2
Umberto Picchini (umberto@maths.lth.se)

7. ABC within MCMC (Marjoram et al. 2003)
Data: y ∈ Y. Realizations y∗ from the SSM, y∗ ∈ Y.
Algorithm 1 a generic iteration of ABC-MCMC (fixed threshold δ)
At r-th iteration
1. generate θ∗ ∼ q(θ|θr), e.g. using Gaussian random walk
2. simulate x∗|θ∗ ∼ p(x|θ∗) and y∗ ∼ p(y|x∗, θ∗)
3. accept (θ∗, y∗) with probability
min 1, Jδ(y,y∗;θ∗)p(y∗|θ∗)π(θ∗)
Jδ(y,yr;θr)p(yr|θr)π(θr)
q(θr|θ∗)
q(θ∗|θr)
p(yr|θr)
p(y∗|θ∗)
then set r = r + 1 and go to 1.
Umberto Picchini (umberto@maths.lth.se)

8. ABC within MCMC (Marjoram et al. 2003)
Data: y ∈ Y. Realizations y∗ from the SSM, y∗ ∈ Y.
Algorithm 2 a generic iteration of ABC-MCMC (fixed threshold δ)
At r-th iteration
1. generate θ∗ ∼ q(θ|θr), e.g. using Gaussian random walk
2. simulate x∗|θ∗ ∼ p(x|θ∗) and y∗ ∼ p(y|x∗, θ∗)
3. accept (θ∗, y∗) with probability
min 1, Jδ(y,y∗;θ∗)p(y∗|θ∗)π(θ∗)
Jδ(y,yr;θr)p(yr|θr)π(θr)
q(θr|θ∗)
q(θ∗|θr)
p(yr|θr)
p(y∗|θ∗)
then set r = r + 1 and go to 1.
Samples are from πδ(θ|y)
or from the exact posterior when δ = 0.
Umberto Picchini (umberto@maths.lth.se)

9. ABC within MCMC (Marjoram et al. 2003)
Data: y ∈ Y. Realizations y∗ from the SSM, y∗ ∈ Y.
Algorithm 3 a generic iteration of ABC-MCMC (fixed threshold δ)
At r-th iteration
1. generate θ∗ ∼ q(θ|θr), e.g. using Gaussian random walk
2. simulate x∗|θ∗ ∼ p(x|θ∗) and y∗ ∼ p(y|x∗, θ∗)
3. accept (θ∗, y∗) with probability
min 1, Jδ(y,y∗;θ∗)p(y∗|θ∗)π(θ∗)
Jδ(y,yr;θr)p(yr|θr)π(θr)
q(θr|θ∗)
q(θ∗|θr)
p(yr|θr)
p(y∗|θ∗)
then set r = r + 1 and go to 1.
Samples are from πδ(θ|y)
or from the exact posterior when δ = 0.
Umberto Picchini (umberto@maths.lth.se)

10. a completely made-up illustration
green: the target posterior; prior distribution is uniform.
Let’s decrease δ progressively...
Umberto Picchini (umberto@maths.lth.se)
0 2 4 6 8 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8

11. Typically we cannot reduce δ as much as we like.
When incurring into high rejection rates we might have to stop at the
pink approximation.
0 2 4 6 8 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
For the “best feasible δ” (pink) we get the MAP pretty much ok.
Tails are awful though...
Umberto Picchini (umberto@maths.lth.se)

12. Suppose we are in a scenario where it’s not feasible to decrease δ
further...What to do?
Here I am borrowing the data cloning idea.
data-cloning was independently introduced in:
1 Doucet, Godsill, Robert. Statistics and Computing (2002)
2 Jacquier, Johannes, Polson. J. Econometrics (2007)
3 popularized in ecology by Lele, Dennis, Lutscher. Ecology
Letters (2007).
Umberto Picchini (umberto@maths.lth.se)

13. Suppose we are in a scenario where it’s not feasible to decrease δ
further...What to do?
Here I am borrowing the data cloning idea.
data-cloning was independently introduced in:
1 Doucet, Godsill, Robert. Statistics and Computing (2002)
2 Jacquier, Johannes, Polson. J. Econometrics (2007)
3 popularized in ecology by Lele, Dennis, Lutscher. Ecology
Letters (2007).
Umberto Picchini (umberto@maths.lth.se)

14. “data cloning” for state-space models
(forget about ABC for the moment)
data: y
likelihood: L(θ; y)
choose an integer K 1 and stack K copies of your data
y(K)
= (y, y, ..., y)
K times
The corresponding posterior is
π(θ|y(K)
) ∝ (L(θ; y(K)
))π(θ)
Consider K independent realizations X(1)
, ..., X(K)
of {Xt}, with
X(k)
= (X
(k)
0 , ..., X
(k)
n ) , k = 1, ..., K
L(θ; y(K)
) =
K
k=1
f(y|X(k)
, θ)p(X(k)
|θ)dX(k)
= (L(θ; y))K
.
use MCMC to sample from π(θ|y(K)
) for “large” K.
Umberto Picchini (umberto@maths.lth.se)

15. Asymptotics, K → ∞ (Jacquier et al. 2007; Lele et al. 2007)
K is the # of data “clones”
when K → ∞ we have...
¯θ = sample mean of MCMC draws from π(θ|y(K)) ⇒ ˆθmle
(whatever the prior!)
K× [sample covariance of draws] from π(θ|y(K)) ⇒ I−1
ˆθmle
the
inverse of the Fisher information of the MLE.
¯θ ⇒ N ˆθmle, K−1 · I−1
ˆθmle
1 Jacquier, Johannes, Polson. J. Econometrics (2007)
2 Lele, Dennis, Lutscher. Ecology Letters (2007).
Umberto Picchini (umberto@maths.lth.se)

16. Our idea
Compensate for the inability to decrease δ by increasing K.
1 Run ABC-MCMC for decreasing δ (fix K = 1, no data-cloning);
2 Stop decreasing δ and start increasing K 1 (data-cloning).
3 distribution shrinks around the MLE (tick vertical line)
Umberto Picchini (umberto@maths.lth.se)
0 2 4 6 8 10
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
initial δ

17. Rationale
Rationale (with abuse of notation):
from ABC theory:
lim
δ→0
πδ(θ|y(K)
) = π(θ|y(K)
)
from data-cloning theory:
lim
K→∞
π(θ|y(K)
) = N(ˆθmle, K−1
· I−1
ˆθmle
)
hence first reduce δ then enlarge K
lim
K→∞
lim
δ→0
πδ(θ|y(K)
) = N(ˆθmle, K−1
· I−1
ˆθmle
)
Umberto Picchini (umberto@maths.lth.se)

18. lim
K→∞
lim
δ→0
πδ(θ|y(K)
) = N(ˆθmle, K−1
· I−1
ˆθmle
)
Now:
of course we can’t really let both δ → 0 and K → ∞
these two criteria compete! Computationally not feasible to
satisfy both.
I have no proof for the quality of the estimates for δ 0 and K
finite.
Umberto Picchini (umberto@maths.lth.se)

19. in Summary:
non-ABC (augmented) target posterior for a SSM:
π(θ, ˜X(K)
|y(K)
) ∝
K
k=1
f(y|X(k)
, θ)p(X(k)
|θ) π(θ)
here ˜X(K) = (X(1), ..., X(K)), each X(k) ∼ p(X|θ) i.i.d.
my ABC data-cloned posterior for a SSM:
πδ(θ, y∗(K)
|y(K)
) ∝
K
k=1
Jδ(y, y∗(k)
, θ)p(X(k)
|θ) π(θ)
as an example: Jδ(y, y∗(k)
; θ) := n
i=1
1
δe−
y∗(k)
i −yi
2
2δ2
Umberto Picchini (umberto@maths.lth.se)

20. Main problem with ABC: for complex models it is difficult to
obtain a decent acceptance rate during ABC-MCMC when δ
“small”.
Idea: set δ to a large (manageable) value, and compensate by
“powering up” the posterior → data-cloning. That is...
1 Preliminary step: use a typical ABC-MCMC with K = 1.
Determine the main mode ˜θ of πδ(θ|y) with δ “not-too-small”
(5% acceptance rate).
2 Start a further ABC-MCMC with K 1 by drawing proposal
using independence Metropolis centred at ˜θ.
3 Increase K progressively...
Umberto Picchini (umberto@maths.lth.se)

21. Algorithm 4 data-cloning ABC (P. 2015)
ABC-MCMC stage K = 1 using adaptive Metropolis random walk AMRW
1. Generate X∗
from p(X|θ∗
) and a corresponding y∗
from SSM. Compute
Jδ(y, y∗
; θ∗
).
2. Generate θ#
:= AMRW(θ∗
, Σ). Generate X#
’s from p(X|θ#
) and corresponding
y#
. Compute Jδ(y, y#
; θ#
).
3. Accept θ∗
with probability
α = min 1,
Jδ(y, y#
; θ#
)
Jδ(y, y∗; θ∗)
×
u1(θ∗
|θ#
, Σ)
u1(θ#|θ∗, Σ)
×
π(θ#
)
π(θ∗)
Data-cloning stage using a Metropolis independent sampler MIS
4. Fetch the maximum ˜θ from ABC-MCMC then do as above but proposing using
θ#
:= MIS(˜θ, ˆΣ).
5. Increase K := K + 1. Generate independently y#(1)
, ..., y#(K)
from p(y|θ#
)
6. Accept proposal with probability
α = min 1,
K
k=1 Jδ(y, y#(k)
; θ#
)
K
k=1 Jδ(y, y∗(k); θ∗)
×
u2(θ∗
|˜θ, ˆΣ)
u2(θ#|˜θ, ˆΣ)
×
π(θ#
)
π(θ∗)
.
Umberto Picchini (umberto@maths.lth.se)

22. Stochastic Gompertz model
dXt = BCe−Ct
Xtdt + σXtdWt, X0 = Ae−B
Used in ecology for population growth, e.g. chicken growth data [Donnet,
Foulley, Samson 2010]
0 5 10 15 20 25 30 35 40
0
1
2
3
4
5
6
7
8
9
12 observations from {log Xt}. X0 assumed known.
We wish to estimate θ = (A, B, C, σ)
Exact MLE available as transition densities are known.
Umberto Picchini (umberto@maths.lth.se)

23. Priors: log A ∼ U(6, 9), log C ∼ U(0.5, 4), σ ∼ LN(0, 0.15)
Umberto Picchini (umberto@maths.lth.se)
0 0.5 1 1.5 2 2.5
x 10
6
6
6.5
7
7.5
8
8.5
9
log A
K=5, δ=0.5, Exact MLE (green)

24. Comparison with exact MLE
0 0.5 1 1.5 2 2.5 3
x 10
6
6
6.5
7
7.5
8
8.5
9
log A
0 0.5 1 1.5 2 2.5 3
x 10
6
1
1.5
2
2.5
3
3.5
4
0 0.5 1 1.5 2 2.5 3
x 10
6
−1
−0.5
0
0.5
1
log σ
True values Exact MLE ABC ((K, δ) = (5, 0.5))
log A 8.01 7.8 (0.486) 7.716 (0.471)
log B(∗) 1.609 1.567 1.550
log C 2.639 2.755 (0.214) 2.872 (0.473)
log σ 0 -0.14 (0.211) -0.251 (0.228)
Table: (*) log ˆB deterministically determined as log(log(ˆA/X0)) as X0 = Ae−B
with
X0 known.
Umberto Picchini (umberto@maths.lth.se)

25. Gompertz state-space model
Yti = log(Xti ) + εti εti ∼ N(0, σ2
ε)
dXt = BCe−CtXtdt + σXtdWt, X0 = Ae−B
12 observations from {Yti }. State {Xt} is unobserved. X0 assumed
known.
Wish to estimate θ = (A, B, C, σ, σε)
Umberto Picchini (umberto@maths.lth.se)

26. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4
5
6
7
8
9
t
Figure: data and three sample trajectories from the estimated state-space model.
True values ABC-DC ((K, δ) = (4, 0.8))
log A 8.01 8.01 (0.567)
log B(*) 1.609 1.611
log C 2.639 3.152 (0.982)
log σ 0 -0.080 (0.258)
log σ −0.799 -0.577 (0.176)
Umberto Picchini (umberto@maths.lth.se)

27. Take-home message
1 Sometimes we want to do MLE but we are unable to...
2 Sometimes we want to go full Bayesian but we can’t...
3 Sometimes even ABC is challenging...
4 There are endless possibilities out there (EP, VB and more...)
5 Working paper:
P. (2015) “Approximate maximum likelihood estimation using
data-cloning ABC‘”, arXiv:1505.06318.
6 blog discussion by Christian P. Robert (2 June)
https://xianblog.wordpress.com
Thank You
Umberto Picchini (umberto@maths.lth.se)

28. Appendix
Appendix
Umberto Picchini (umberto@maths.lth.se)

29. Appendix
“Likelihood free” Metropolis-Hastings
Suppose at a given iteration of Metropolis-Hastings we are in the
(augmented)-state position (θ#, x#) and wonder whether to move (or
not) to a new state (θ , x ). The move is generated via a proposal
distribution “q((θ#, x#) → (x , θ ))”.
e.g. “q((θ#, x#) → (x , θ ))” = u(θ |θ#)v(x | θ );
move “(θ#, x#) → (θ , x )” accepted with probability
α(θ#,x#)→(x ,θ ) = min 1,
π(θ )π(x |θ )π(y|x , θ )q((θ , x ) → (θ#, x#))
π(θ#)π(x#|θ#)π(y|x#, θ#)q((θ#, x#) → (θ , x ))
= min 1,
π(θ )π(x |θ )π(y|x , θ )u(θ#|θ )v(x# | θ#)
π(θ#)π(x#|θ#)π(y|x#, θ#)u(θ |θ#)v(x | θ )
now choose v(x | θ) ≡ π(x | θ)
= min 1,
π(θ )π(x |θ )π(y|x , θ )u(θ#|θ )
π(x# | θ#)
π(θ#)π(x#|θ#)π(y|x#, θ#)u(θ |θ#)
π(x | θ )
This is likelihood–free! And we only need to know how to generate xUmberto Picchini (umberto@maths.lth.se)

30. Appendix
“Likelihood free” Metropolis-Hastings
Suppose at a given iteration of Metropolis-Hastings we are in the
(augmented)-state position (θ#, x#) and wonder whether to move (or
not) to a new state (θ , x ). The move is generated via a proposal
distribution “q((θ#, x#) → (x , θ ))”.
e.g. “q((θ#, x#) → (x , θ ))” = u(θ |θ#)v(x | θ );
move “(θ#, x#) → (θ , x )” accepted with probability
α(θ#,x#)→(x ,θ ) = min 1,
π(θ )π(x |θ )π(y|x , θ )q((θ , x ) → (θ#, x#))
π(θ#)π(x#|θ#)π(y|x#, θ#)q((θ#, x#) → (θ , x ))
= min 1,
π(θ )π(x |θ )π(y|x , θ )u(θ#|θ )v(x# | θ#)
π(θ#)π(x#|θ#)π(y|x#, θ#)u(θ |θ#)v(x | θ )
now choose v(x | θ) ≡ π(x | θ)
= min 1,
π(θ )π(x |θ )π(y|x , θ )u(θ#|θ )
π(x# | θ#)
π(θ#)π(x#|θ#)π(y|x#, θ#)u(θ |θ#)
π(x | θ )
This is likelihood–free! And we only need to know how to generate xUmberto Picchini (umberto@maths.lth.se)

31. Appendix
“Likelihood free” Metropolis-Hastings
Suppose at a given iteration of Metropolis-Hastings we are in the
(augmented)-state position (θ#, x#) and wonder whether to move (or
not) to a new state (θ , x ). The move is generated via a proposal
distribution “q((θ#, x#) → (x , θ ))”.
e.g. “q((θ#, x#) → (x , θ ))” = u(θ |θ#)v(x | θ );
move “(θ#, x#) → (θ , x )” accepted with probability
α(θ#,x#)→(x ,θ ) = min 1,
π(θ )π(x |θ )π(y|x , θ )q((θ , x ) → (θ#, x#))
π(θ#)π(x#|θ#)π(y|x#, θ#)q((θ#, x#) → (θ , x ))
= min 1,
π(θ )π(x |θ )π(y|x , θ )u(θ#|θ )v(x# | θ#)
π(θ#)π(x#|θ#)π(y|x#, θ#)u(θ |θ#)v(x | θ )
now choose v(x | θ) ≡ π(x | θ)
= min 1,
π(θ )π(x |θ )π(y|x , θ )u(θ#|θ )
π(x# | θ#)
π(θ#)π(x#|θ#)π(y|x#, θ#)u(θ |θ#)
π(x | θ )
This is likelihood–free! And we only need to know how to generate xUmberto Picchini (umberto@maths.lth.se)