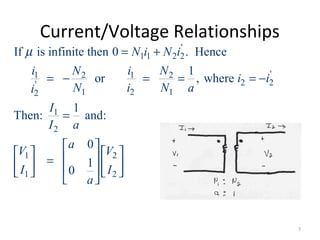
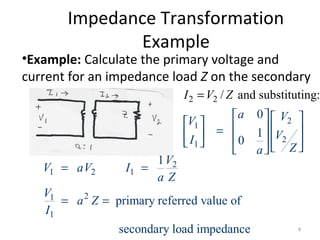
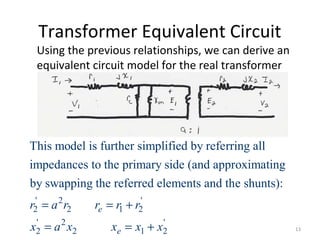
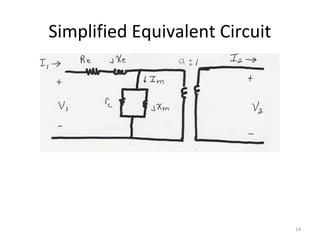
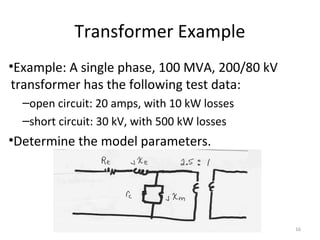
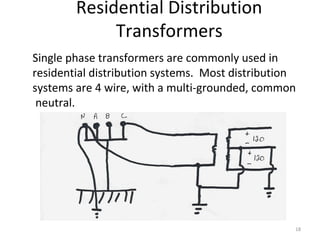
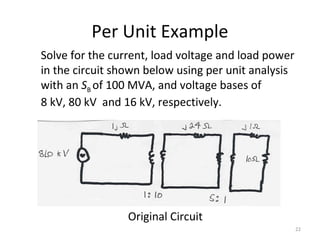
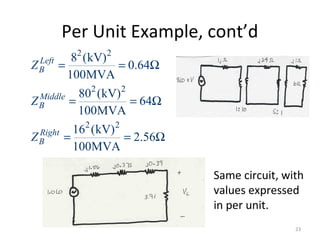
This document provides an overview of transformers and per unit analysis in power systems. Key points include: 1) Transformers are used to transfer power between different voltage levels in power systems. An ideal transformer model and a more accurate model accounting for losses and leakage flux are described. 2) Per unit analysis is introduced as a method to normalize variables across different voltage bases. All values are expressed relative to selected system base values. 3) Examples of per unit analysis are provided for both single phase and three phase systems, showing how quantities can be converted between per unit and actual values.

1. EE 369
POWER SYSTEM ANALYSIS
Lecture 8
Transformers, Per Unit
Tom Overbye and Ross Baldick
1

2. Announcements
• For lectures 8 to 10 read Chapter 3
HW 6 is problems 5.2, 5.4, 5.7, 5.9, 5.14, 5.16,
5.19, 5.26, 5.31, 5.32, 5.33, 5.36; case study
questions chapter 5 a, b, c, d, is due Thursday,
10/15.
Homework 7 is 5.8, 5.15, 5.17, 5.24, 5.27,
5.28, 5.29, 5.34, 5.37, 5.38, 5.43, 5.45; due
10/22.
2

3. Transformers Overview
• Power systems are characterized by many
different voltage levels, ranging from 765 kV
down to 240/120 volts.
• Transformers are used to transfer power
between different voltage levels.
• The ability to inexpensively change voltage
levels is a key advantage of ac systems over dc
systems.
• In this section we’ll development models for
the transformer and discuss various ways of
connecting three phase transformers. 3

4. Ideal Transformer
First we review the voltage/current relationships
for an ideal transformer
– no real power losses
– magnetic core has infinite permeability
– no leakage flux
We’ll define the “primary” side of the
transformer as the side that usually receives
power from a line etc, and the secondary as the
side that usually delivers power to a load etc:
– primary is usually the side with the higher voltage,
but may be the low voltage side on a generator step-
up transformer. 4

5. Ideal Transformer Relationships
1
1 1 2 2
1 2
1 1 2 2
1 2 1 1
1 2 2 2
Assume we have flux in magnetic material.
Then flux linking coil 1 having turns is:
, and similarly
,
= turns ratio
m
m m
m m
m
N
N N
d dd d
v N v N
dt dt dt dt
d v v V N
a
dt N N V N
φ
λ φ λ φ
φ φλ λ
φ
= =
= = = =
= = ⇒ = =
Note that I2 and I2’
are in opposite directions
5

6. Current Relationships
'
1 1 2 2
'
1 1 2 2
'
1 1 2 2
To get the current relationships use ampere's law
with path around core having total length :
mmf
Assuming uniform flux density in the core
having area ,
L
d N i N i
H L N i N i
B L
N i N i
A
µ
Γ
= = +
× = +
×
= +
∫ H LgÑ
'
1 1 2 2
then B A
L
N i N i
A
φ
φ
µ
= ×
×
= +
× 6

7. Current/Voltage Relationships
'
1 1 2 2
'1 2 1 2
2 2'
1 2 12
1
2
1 2
1 2
If is infinite then 0 . Hence
1
or , where
1
Then: and:
0
1
0
N i N i
i N i N
i i
N i N ai
I
I a
a
V V
I I
a
µ = +
= − = = = −
=
 
    =       
 
7

8. Impedance Transformation
Example
•Example: Calculate the primary voltage and
current for an impedance load Z on the secondary
2
1
2
1
2 2 / and substituting:
0
1
0
a VV
VI
Za
I V Z
     =         
=

2
1 2 1
21
1
1
primary referred value of
secondary load impedance
V
V aV I
a Z
V
a Z
I
= =
= =
8

9. Real Transformers
• Real transformers
– have losses
– have leakage flux
– have finite permeability of magnetic core
• Real power losses
– resistance in windings (I2
R)
– core losses due to eddy currents and hysteresis
9

10. Transformer Core losses
Eddy currents arise because of changing flux in core.
Eddy currents are reduced by laminating the core
Hysteresis losses are proportional to area of BH curve
and the frequency
These losses are reduced
by using material with a
“thin” BH curve
10

11. Effect of Leakage Flux
1 1 1 1
2 2 2 2
1 1 1 2 2
Not all flux is within the transformer core
, where is the coil 1 leakage flux,
, where is the coil 2 leakage flux,
Assuming a linear magnetic medium we get
l m l
l m l
l l l l
N
N
L i L i
λ λ φ λ
λ λ φ λ
λ λ
= +
= +
@ @ 2
2
2
'
1
1 1 1 1 1
1
'
'
2 2 2 2 2
, including winding
resistance ,
, including resistance .
m
l
m
l
ddi
v ri L N
dt dt
r
di d
v r i L N r
dt dt
φ
φ
= + +
= + +
11

12. Effect of Finite Core Permeability
m
1 1 2 2 m
m 2
1 2
1 1
1 m
Finite core permeability means a non-zero mmf
is required to maintain in the core
,
where is the reluctance.
This effect is usually modeled as a magnetizing current
N i N i R
R
R N
i i
N N
N
i i
φ
φ
φ
− =
= +
= + 2 m
2 m
1 1
where ,
modeled by resistance and inductance.
R
i i
N N
φ
=
12

13. Transformer Equivalent Circuit
Using the previous relationships, we can derive an
equivalent circuit model for the real transformer
' 2 '
2 2 1 2
' 2 '
2 2 1 2
This model is further simplified by referring all
impedances to the primary side (and approximating
by swapping the referred elements and the shunts):
e
e
r a r r r r
x a x x x x
= = +
= = + 13

14. Simplified Equivalent Circuit
14

15. Calculation of Model Parameters
The parameters of the model are determined
based upon:
– nameplate data: gives the rated voltages and power
– open circuit test: rated voltage is applied to primary
with secondary open; measure the primary current
and losses (the test may also be done applying the
rated voltage to the secondary, calculating the values,
then referring the values back to the primary side).
– short circuit test: with secondary shorted, apply
(lower than rated) voltage to primary to get rated
primary current to flow; measure voltage and losses.15

16. Transformer Example
•Example: A single phase, 100 MVA, 200/80 kV
transformer has the following test data:
–open circuit: 20 amps, with 10 kW losses
–short circuit: 30 kV, with 500 kW losses
•Determine the model parameters.
16

17. Transformer Example, cont’d
2 2 2
2 2
2 2 2
rated
100MVA 30 kV
500 A, 60
200kV 500 A
500 kW / 500,000/(500) 2 ,
Hence 60 2 60
( ) (200) (kV)
4M
10 kW
sc e e
sc e sc e sc sc
e
c
oc
e
I R jX
P R I R P I
X
V
R
P
R
= = + = = Ω
= = ⇒ = = = Ω
= − = Ω
≈ = = Ω
+
From the short circuit test
From the open circuit test
rated 200 kV
10,000 10,000
20 A
e m m
oc
V
jX jX X
I
+ ≈ = = Ω = Ω
17

18. Residential Distribution
Transformers
Single phase transformers are commonly used in
residential distribution systems. Most distribution
systems are 4 wire, with a multi-grounded, common
neutral.
18

19. Per Unit Calculations
A key problem in analyzing power systems is
the large number of transformers.
– It would be very difficult to continually have to refer
impedances to the different sides of the
transformers
This problem is avoided by a normalization of
all variables.
This normalization is known as per unit
analysis. actual quantity
quantity in per unit
base value of quantity
=
19

20. Per Unit Conversion Procedure, 1φ
1. Pick a 1φ VA base for the entire system, SB
2. Pick a voltage base for each different voltage
level, VB. Voltage bases are related by
transformer turns ratios. Voltages are line to
neutral.
3. Calculate the impedance base, ZB= (VB)2
/SB
4. Calculate the current base, IB = VB/ZB
5. Convert actual values to per unit
Note, per unit conversion affects magnitudes, not
the angles. Also, per unit quantities no longer have
units (i.e., a voltage is 1.0 p.u., not 1 p.u. volts) 20

21. Per Unit Solution Procedure
1. Convert to per unit (p.u.) (many problems
are already in per unit)
2. Solve
3. Convert back to actual as necessary
21

22. Per Unit Example
Solve for the current, load voltage and load power
in the circuit shown below using per unit analysis
with an SB of 100 MVA, and voltage bases of
8 kV, 80 kV and 16 kV, respectively.
Original Circuit
22

23. Per Unit Example, cont’d
2 2
2 2
2 2
8 (kV)
0.64
100MVA
80 (kV)
64
100MVA
16 (kV)
2.56
100MVA
Left
B
Middle
B
Right
B
Z
Z
Z
= = Ω
= = Ω
= = Ω
Same circuit, with
values expressed
in per unit.
23

24. Per Unit Example, cont’d
2
*
1.0 0
0.22 30.8 p.u. (not amps)
3.91 2.327
1.0 0 0.22 30.8
p.u.
0.189 p.u.
1.0 0 0.22 30.8 30.8 p.u.
L
L
L L L
G
I
j
V
V
S V I
Z
S
∠ °
= = ∠ − °
+
= ∠ ° − ∠ − °×2.327∠90°
= 0.859∠ − 30.8°
= = =
= ∠ °× ∠ ° = 0.22∠ °
24

25. Per Unit Example, cont’d
To convert back to actual values just multiply the
per unit values by their per unit base
Actual
Actual
Actual
Middle
Actual
Middle
0.859 30.8 16 kV 13.7 30.8 kV
0.189 0 100 MVA 18.9 0 MVA
0.22 30.8 100 MVA 22.0 30.8 MVA
100 MVA
1250 Amps
80 kV
0.22 30.8 275 30.8
L
L
G
B
V
S
S
I
I
= ∠ − °× = ∠ − °
= ∠ °× = ∠ °
= ∠ °× = ∠ °
= =
= ∠ − °×1250 = ∠ − ° Α
25

26. Three Phase Per Unit
1. Pick a 3φ VA base for the entire system,
2. Pick a voltage base for each different
voltage level, VB,LL. Voltages are line to line.
3. Calculate the impedance base
Procedure is very similar to 1φ except we use a 3φ
VA base, and use line to line voltage bases
3
BS φ
2 2 2
, , ,
3 1 1
( 3 )
3
B LL B LN B LN
B
B B B
V V V
Z
S S Sφ φ φ
= = =
Exactly the same impedance bases as with single phase using
the corresponding single phase VA base and voltage base!26

27. Three Phase Per Unit, cont'd
4. Calculate the current base, IB
5. Convert actual values to per unit
3 1 1
3 1
B B
, , ,
3
3 3 3
B B B
B LL B LN B LN
S S S
I I
V V V
φ φ φ
φ φ
= = = =
Exactly the same current bases as with single phase!
27

28. Three Phase Per Unit Example
•Solve for the current, load voltage and load
power in the previous circuit, assuming:
–a 3φ power base of 300 MVA,
–and line to line voltage bases of 13.8 kV, 138 kV
and 27.6 kV (square root of 3 larger than the 1φ
example voltages)
–the generator is Y-connected so its line to line
voltage is 13.8 kV.
Convert to per unit
as before.
Note the system is
exactly the same!
28

29. 3φ Per Unit Example, cont'd
2
*
1.0 0
0.22 30.8 p.u. (not amps)
3.91 2.327
1.0 0 0.22 30.8
p.u.
0.189 p.u.
1.0 0 0.22 30.8 30.8 p.u.
L
L
L L L
G
I
j
V
V
S V I
Z
S
∠ °
= = ∠ − °
+
= ∠ ° − ∠ − °×2.327∠90°
= 0.859∠ − 30.8°
= = =
= ∠ °× ∠ ° = 0.22∠ °
Again, analysis is exactly the same!
29

30. 3φ Per Unit Example, cont'd
L
Actual
Actual
L
Actual
G
Middle
B
Actual
Middle
0.859 30.8 27.6 kV 23.8 30.8 kV
0.189 0 300 MVA 56.7 0 MVA
0.22 30.8 300 MVA 66.0 30.8 MVA
300 MVA
125 (same cu0 Amps
3138 kV
0.22 30
rrent
8
!)
.
V
S
S
I
I
= ∠ − °× = ∠ − °
= ∠ °× = ∠ °
= ∠ °× = ∠ °
= =
= ∠ − °× Amps 275 30.81250 = ∠ − ° Α
Differences appear when we convert back to actual values
30