The document discusses the equivalent circuit model of a transformer. 1) The equivalent circuit accounts for copper losses in the primary and secondary windings, eddy current losses in the core, hysteresis losses in the core, and leakage fluxes between the primary and secondary coils. 2) Key components of the equivalent circuit model include resistances to represent copper losses, inductances to represent the effects of mutual and leakage fluxes, and a resistance and inductance in parallel to represent core losses and excitation. 3) Test procedures for determining the parameters of the equivalent circuit model are described, including open circuit and short circuit tests to calculate resistance, reactance, and impedance values.

1. ENERGY CONVERSION ONE
(Course 25741)
Chapter Two
TRANSFORMERS
…continued

2. Equivalent Circuit of Transformer
• Major Items to be considered in Construction of
Transformer Model:
• Copper losses (in primary & Secondary
winding) ~ I²
• Eddy current losses (in core) ~ V²
• Hysteresis losses (in core) a complex nonlinear
function of applied V
• Leakage flux : φLP & φLS, these fluxes produce
self-inductance in primary & secondary coils

3. Equivalent Circuit of Transformer
• Exact Eq. cct. Model for Real Transformer
• Copper losses modeled by resistances Rp & Rs
• As discussed before:
• φp=φm+φLp φp; total av. Primary flux
• φS=φm+φLS φS; total av. Secondary flux
• where φm; flux linking both P & S
φLp; primary leakage flux
φLS; secondary leakage flux
The average primary (& Secondary) flux, each, is
divided into two components as:
mutual flux & leakage flux

4. Equivalent Circuit of Transformer
• Based on application of these components,
Faraday’s law for primary circuit can be
expressed as:
• Vp(t)=Np dφp/dt = Np dφM/dt + Np dφLp/dt or:
• Vp(t)=ep(t) + eLp(t) similarly for secondary:
• Vs(t)=Ns dφs/dt = Ns dφM/dt + Ns dφLs/dt or:
• Vs(t)=es(t) + eLs(t)
• primary & secondary voltages due to mutual
flux :
ep(t) = Np dφM/dt es(t)= Ns dφM/dt

5. Equivalent Circuit of Transformer
• Note : ep(t)/Np = dφM/dt =es(t)/Ns
• ep(t)/es(t) = Np / Ns =a
• while eLp(t) = Np dφLp/dt & eLs(t)= Ns dφLs/dt
if р = permeance of leakage flux path
• φLp=(p Np) ip & φLs=(p Ns) is
• eLp(t) = Np d/dt (p Np) ip = Np²p dip/dt
• eLs(t) = Ns d/dt (p Ns) is = Ns²p dis/dt
Defining:Lp = Np²p primary leakage inductanc
Ls = Ns²p secondary leakage inductance

6. Equivalent Circuit of Transformer
• eLp(t)=Lp dip/dt
• eLs(t)=Ls dis/dt
• Therefore leakage flux can be modeled by primary & secondary
leakage inductances in equivalent electric circuit
• Core Excitation that is related to the flux linking both windings
(φm; flux linking both P & S) should also be realized in modeling
• im (in unsaturated region) ~ e (voltage applied to core)
and lag applied voltage by 90◦ modeled by an inductance Lm
(reactance Xm)
• Core-loss current ie+h is ~ voltage applied & It can be modeled
by a resistance Rc across primary voltage source
• Note: these currents nonlinear therefore: Xm & Rc are best
approximation of real excitation

7. Equivalent Circuit of Transformer
• The resulted equivalent circuit is shown:
• Voltage applied to core = input voltage-internal
voltage drops of winding

8. Equivalent Circuit of Transformer
• to analyze practical circuits including Transformers, it
is required to have equivalent cct. at a single voltage
• Therefore circuit can be referred either to its primary
side or secondary side as shown:

9. Equivalent Circuit of Transformer
• Approximate Equivalent Circuits of a Transformer
• in practice in some studies these models are more
complex than necessary
• i.e. the excitation branch add another node to
circuit, while in steady state study, current of this
branch is negligible
• And cause negligible voltage drop in Rp & Xp
• Therefore approximate eq. model offered as:
•

10. Equivalent Circuit of Transformer
Approximate transformer models
• a- referred to primary
• b- referred to secondary
• c- with no excitation branch referred to p
• d- with no excitation branch referred to s

11. Determination of Transformer Eq. cct.
parameters
• Approximation of inductances & resistances obtained
by two tests:
open circuit test & short circuit test
1- open circuit test : transformer’s secondary winding
is open circuited, & primary connected to a full-rated
line voltage, Open-circuit test connections as below:

12. Determination of Transformer Eq. cct.
parameters
• Input current, input voltage & input power measured
• From these can determine p.f., input current, and
consequently both magnitude & angle of excitation
impedance (RC, and XM)
• First determining related admittance and
Susceptance:
GC=1/RC & BM=1/XM  YE=GC-jBM=1/RC -1/XM
• Magnitude of excitation admittance referred to primary
circuit : |YE |=IOC/VOC
• P.f. used to determine angle,
• PF=cosθ=POC/[VOC . IOC]
• θ=cos‾1 {POC/[VOC . IOC]}

13. Determination of Transformer Eq.
cct. parameters
• Thus: YE = IOC/VOC = IOC / VOC
• Using these equations RC & XM can be
determined from O.C. measurement
PF
1
cos






14. Determination of Transformer Eq. cct.
parameters
• Short-Circuit test : the secondary terminals of
transformer are short circuited, and primary
terminals connected to a low voltage source:
• Input voltage adjusted until current in s.c.
windings equal to its rated value

15. Determination of Transformer Eq.
cct. parameters
• The input voltage, current and power are again measured
• Since input voltage is so low during short-circuited test, negligible current
flows through excitation branch
• Therefore, voltage drop in transformer attributed to series elements
• Magnitude of series impedances referred to primary side of transformer is:
|ZSE| = VSC/ ISC , PF=cosθ=PSC/[VSC ISC]
• θ=cos‾1 {PSC/[VSC ISC]}
• ZSE= VSC / ISC = VSC/ ISC
• series impedance ZSE is equal to:
• ZSE=Req+jXeq = (RP+ a²RS) + j(XP+a²XS)
• It is possible to determine the total series impedance referred to primary side
, however difficult to split series impedance into primary & secondary
components although it is not necessary to solve problem
• These same tests may also be performed on secondary side of transformer



0
 


16. Determination of Transformer Eq.
cct. parameters
• Determine Equivalent cct.
Impedances of a 20 kVA,
8000/240 V, 60 Hz
transformer
• O.C. & S.C. measurements
shown
• P.F. in O.C. is:
• PF=cosθ=POC/[VOCIOC]=
400 W/ [8000V x 0.214A]
=0.234 lagging
O.C. test
(on primary)
S.C. test
(on primary)
VOC=8000V VSC=489V
IOC=0.214A ISC=2.5 A
POC=400W PSC=240W

17. Determination of Transformer Eq.
cct. parameters
• excitation impedance:
• YE=IOC/VOC
= 0.214 A / 8000 V
= 0.0000268
= 0.0000063 – j 0.0000261 = 1/RC- j 1/XM
• Therefore:
• RC=1/ 0.0000063 = 159 kΩ
• XM= 1/0.0000261=38.4 kΩ
PF
1
cos


234
.
0
cos 1





 
5
.
76

18. Determination of Transformer Eq.
cct. parameters
• PF in sc test:
PF=cosθ = PSC/[VSCISC]=240W/ [489x2.5]=0.196 lagging
• Series impedance:
ZSE=VSC/ISC
= 489 V/ 2.5 A =195.6
=38.4 +j 192 Ω
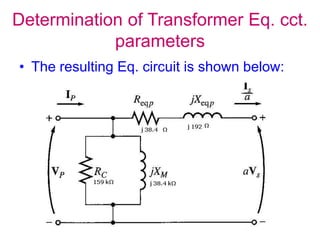
• The Eq. resistance & reactance are :
• Req=38.4 Ω , Xeq=192 Ω
PF
1
cos



7
.
78
 
7
.
78


19. Determination of Transformer Eq. cct.
parameters
• The resulting Eq. circuit is shown below:

20. The Per Unit System For Modeling
• As seen in last Example, solving cct. containing
transformers requires tedious operation to refer all
voltages to a common level
• In another approach, the need mentioned above is
eliminated& impedance transformation is avoided
• That method is known as per-unit system of measurement
• there is also another advantage, in application of per-
unit : as size of machinery & Transformer varies its
internal impedances vary widely, thus a 0.1 Ω cct.
Impedance may not be adequate & depends on
device’s voltage and power ratings

21. The Per Unit System For Modeling
• In per unit system the voltages, currents,
powers, impedance and other electrical
quantities not measured in SI units system
• However it is measured and define as a
decimal fraction of some base level
• Any quantity can be expressed on pu basis
Quantity in p.u. =
Actual Value / base value of quantity

22. The Per Unit System For Modeling
• Two base quantities selected & other base quantities
can be determined from them
• Usually; voltage, & power
• Pbase,Qbase, or Sbase = Vbase Ibase
• Zbase= Vbase/Ibase
• Ybase=Ibase/Vbase
• Zbase=(Vbase)² / Sbase
• In a power system, bases for power & voltage
selected at a specific point, power base remain
constant, while voltage base changes at every
transformer

23. The Per Unit System For Modeling
• Example: A simple power system shown in
Figure below:
• Contains a 480 V generator connected to an
ideal 1:10 step up transformer, a transmission
line, an ideal 20:1 step-down transformer, and a
load

24. The Per Unit System For Modeling
Example …
• Impedance of line 20+j60Ω,impedance of load
• Base values chosen as 480 V and 10 kVA at genertor
(a) Find bas voltage, current, impedance, and power
at every point in power system
(b) convert this system to its p.u. equivalent cct.
(c) Find power supplied to load in this system
(d) Find power lost in transmission line
(a) At generator: Ibase=Sbase/Vbase 1=10000/480=20.83 A
Zbase1=Vbase1/Ibase1=480/20.83=23.04 Ω
• Turn ratio of transformer T1 , a=1/10 =0.1 so base
voltage at line Vbase2=Vbase1/a=480/0.1=4800 V

 
30
10

25. The Per Unit System For Modeling
Example …
• Sbase2=10 kVA
• Ibase2=10000/4800=2.083 A
• Zbase2=4800 V/ 2.083 A = 2304 Ω
• Turn ratio of transformer T2 is a=20/1=20, so
voltage base at load is:
• Vbase3=Vbase2/a =4800/20= 240 V
• Other base quantities are:
• Sbase3=10 kVA
• Ibase3=10000/240=41.67 A
• Zbase3=240/41.67 = 5.76 Ω

26. The Per Unit System For Modeling
Example …
(b) to build the pu equivalent cct. Of power system, each
cct parameter divided by its base value
• VG,pu=
• Zline,pu=(20+j60)/2304=0.0087+j0.0260 pu
• Zload,pu=
• Per unit equivalent cct of PWR. SYS. Shown below:
pu


0
0
.
1
480
/
0
480 


pu


0
736
.
1
76
.
5
/
30
10 



27. The Per Unit System For Modeling
Example …
(c) current flowing in:
• Ipu=Vpu/Ztot,pu=
pu
• Per unit power of load :
Pload,pu =Ipu²Rpu=(0.569)²(1.503)=0.487
• actual power supplied to load:
• Pload=Pload,puSbase=0.487 x 10000=4870 W
(d) power loss in line:
• Pline loss,pu =Ipu²Rline,pu=(0.569)²(0.0087)=0.00282
• Pline= Pline loss,pu Sbase= (0.00282)(10000)=28.2 W




6
.
30
569
.
0
894
.
0
512
.
1
0
1
)
30
736
.
1
(
)
026
.
0
0087
.
0
(
0
1










j
j