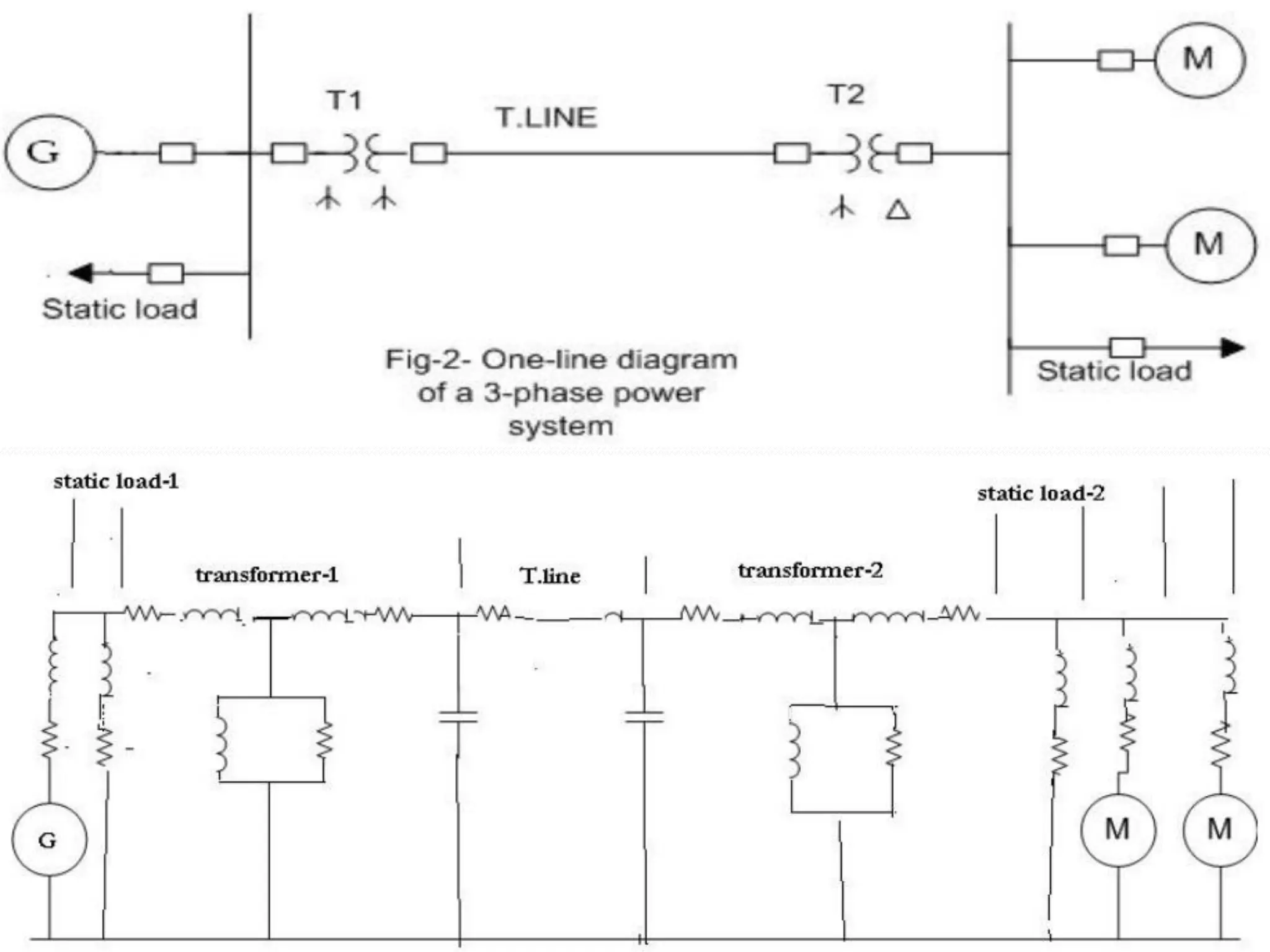
The document covers an introductory course on power system analysis, focusing on circuit constants, power system representation, fault analysis, and stability. Key topics include one-line diagrams, impedance and reactance diagrams, per-unit quantities, and the selection of base values for calculations. It also explains examples of transformer connections and presents formulas for per-unit impedance calculations.

1. Power System Analysis
Presented By: Engr. FAZAL UR REHMAN
Lecturer Electrical KPTEVTA
Visiting Lecturer COMWAVE INSTITUTE ISLAMABAD

2. Course Objectives
 This course is focused on
 Generalized Circuit Constants
 Representation of Power System
 Symmetrical Three Phase Faults
 Symmetrical Components
 Unsymmetrical Faults and
 Power System Stability.

3. Today's Topics
 Representation of Power System
 One-line diagram,
 Impedance and reactance diagram,
 Percent or per-unit quantities,
 Selection of base and
 Change in base of p.u. quantities

4. One-line diagram
 Single line diagram is the representation of a power
system using the simple symbol for each component
connected through a single line between them.
 The single line diagram of a power system is the
network which shows the main connections and
arrangement of the system components along with
their data (such as output rating, voltage, resistance
and reactance, etc.).

5.  It is not necessary to show all the components of the
system on a single line diagram, e.g., circuit breaker
need not be shown in the load flow study but are the
must for a protection study.
 In the single line diagram, the system component is
usually drawn in the form of their symbols.
 Generator and transformer connections, star, delta and
neutral earthing are indicated by symbols drawn by
the side of the representation of these elements.

6. Impedance Diagram
 It is difficult to draw the line diagram of the few
components. So for simplification, the impedance
diagram is used for representing the power system
components.
 In impedance diagram, each component is represented
by its equivalent circuit, e.g., the synchronous
generator at the generating station by a voltage source
in series with the resistance and reactance,
 The transformer by a nominal ∏-equivalent circuit.
 The load is assumed to be passive and are represented
by a resistive and inductive reactance in the series.

7.  The diagram shown below is the balanced 3-phase
diagram.
 It is also called positive sequence diagram.
 Three separate diagrams are also used for representing
the positive, negative and zero sequence networks.
 The three separate impedance diagrams are used in
the short circuit for the studies of unsymmetrical fault.

8. Reactance Diagram
 Reactance diagram is drawn by neglecting the effective
resistance of generator armature, transformer winding
resistance, transmission line resistance line charging
and the magnetizing circuit of transformers.
 The reactance diagram gives an accurate result for
many power system studies, such as short-
circuit studies, etc.

9.  It is considered that if the resistance is less than one-
third of the reactance, and resistance is ignored, then
the error introduced will be not more than 5 %.

11. Percent or per-unit quantities
 Basic Units ƒ
 The 4 basic electrical quantities are:
 Voltage V (volt)
 Current I (amp)
 Impedance Z (ohm)
 Power S (VA) ƒ
 For single-phase circuits, V(volt) = Z(ohm) × I(amp);
 S (VA) = V(volt) × I(amp)*

12.  In per unit notation, the physical quantity is In per
unit notation, the physical quantity is expressed as a
fraction of the reference value, i.e.
per unit value = actual value/base value
V(in per unit) = V(in kV)/V base (in kV)
 Where the base value is a reference value for
magnitude.

13.  For example: 150 amps expressed in the per unit system
with a base value of 200 amps is a per unit current of
0.75:
 Ipu = I/Ib
 Ipu = 150A/200A
 Ipu = 0.75

14.  In per unit notation we would like to keep the basic
relations:
Vpu = Zpu Ipu;
Spu = Vpu I pu
 ƒ
Hence the base quantities should be chosen such that
Base voltage(VB)=base impedance (Z)×base current (IB)
Base power (SB) = Base voltage (VB ) base Current (IB)

15.  Thus only two only two of the base quantities can be of
the base quantities can be arbitrarily chosen,
 The other two will be found out using calculation on
the basis of standard equations.
 It is common practice to specify base power (SB ) and
base voltage (VB) ƒ
 Then it follows
Base current IB = SB/VB
Base impedance ZB = VB/IB =VB
2 /SB

16.  An equivalent way to express the per unit value is the
percentage value
Where Percentage value = per unit value × 100% ƒ
 However, percentage values are not so convenient to
use since
Vpercent ≠ Zpercent × Ipercent

17.  Given V o 100∠30 , Z = 3 + j4 = 5∠53.1o Ω ƒ
Find the
current active, reactive, apparent power & power
factor?
 Take for example Base power SB = 1 kVA
Base voltage VB = 100 V
 Then Base current IB = SB/VB = 10 A
 Base impedance ZB = VB/IB = 10 Ω
 Given V = 100 ∠30o V = 1.0 ∠30o p.u.
Z = 5∠53.1o Ω = 0.5∠53.1o p.u

24. Selection of base

25. Change in base of p.u. quantities
 For example: the same 0.75 pu of current expressed in
the previous base of 200 amps will be equal to 0.6 pu
when expressed in a new base of 250 amps:
 Ipu new = Ipu old (Ib old/Ib new)
 Ipu new =0.75(200A/250A)
 Ipu new = 0.6 pu

26.  For example, the most common per unit impedance
and percent impedance base change formula you
typically see is the old per unit impedance (or old
percent impedance) multiplied by the new power base
then divided by the old power base:
OR


28. EXAMPLE OF CIRCUITS
CONNECTED BY TRANSFORMERS

30. Per unit impedance of 3-winding
transformers
 Generally, large power transformers have three
windings. The third winding is known as a tertiary
winding which may be used for the following purposes
1. To supply a load at a voltage different from the
secondary voltage.
2. To provide a low impedance for the flow of certain
abnormal currents, such a third harmonic currents.
3. To provide for the excitation of a regulating
transformer.

31.  Note: When one winding is left open, the three
winding transformer behaves as two winding
transformer and standard short circuit tests can be
used to evaluate per unit leakage impedances which
are defined as follows
 Zps = per unit leakage impedance measured from
primary with secondary shorted and tertiary open.
 Zpt = per unit leakage impedance measured from
primary with tertiary shorted and secondary open.

32.  Zst = per unit leakage impedance measured from
secondary with tertiary shorted and primary pen.
 Zps = Zp + Zs ……………(a)
 Zpt = Zp + Zt ………………(b)
 Zst = Zs + Zt ………………(c)
Where Zp, Zs , and Zt : the impedances of primary, secondary
and tertiary.
 Solving these equations we find
 Zp = ½ ( Zps + Zpt- Zst) ……..(d)
 Zs = ½ ( Zps + Zst-Zpt) ……….. (e)
 Zt = ½ ( Zpt + Zst – Zps ) ………..(f)
The impedances Zp, Zs , and Zt of the three windings are
connected in star .

33. EXAMPLE OF 3 WINDING
TRANSFORMER
 The 3 phase rating of 3 winding transformer are:
Primary: Star-connected, 66KV ,15MVA.
Secondary: Star-connected ,13.2KV, 10MVA
Tertiary: Delta- connected ,2.3KV,5MVA.
Neglecting resistance, the leakage impedances are Zps
= 7% on 15 Mva, 66 kv base Zpt = 9% on 15 Mva, 66 kv
base Zst = 8% on 10 Mva, 13.2 kv base
Find the per unit impedances of the star connected
equivalent circuit for a base of 15 Mva, 66 kv in the
primary circuit?

34.  Solution: With the base 15 Mva, 66 kv
 Sbase = 15 Mva for all three terminals is the same and
Vb1 = 66 kv Vb2 = 13.2 kv Vb3 = 2.3 kv
 Zps = 0.07 (no change) Zpt = 0.09 (no change)
Zst = 0.08 ×(15/10)=0.12

35. THANKS FOR WATCHING
ANY QUESTION...?