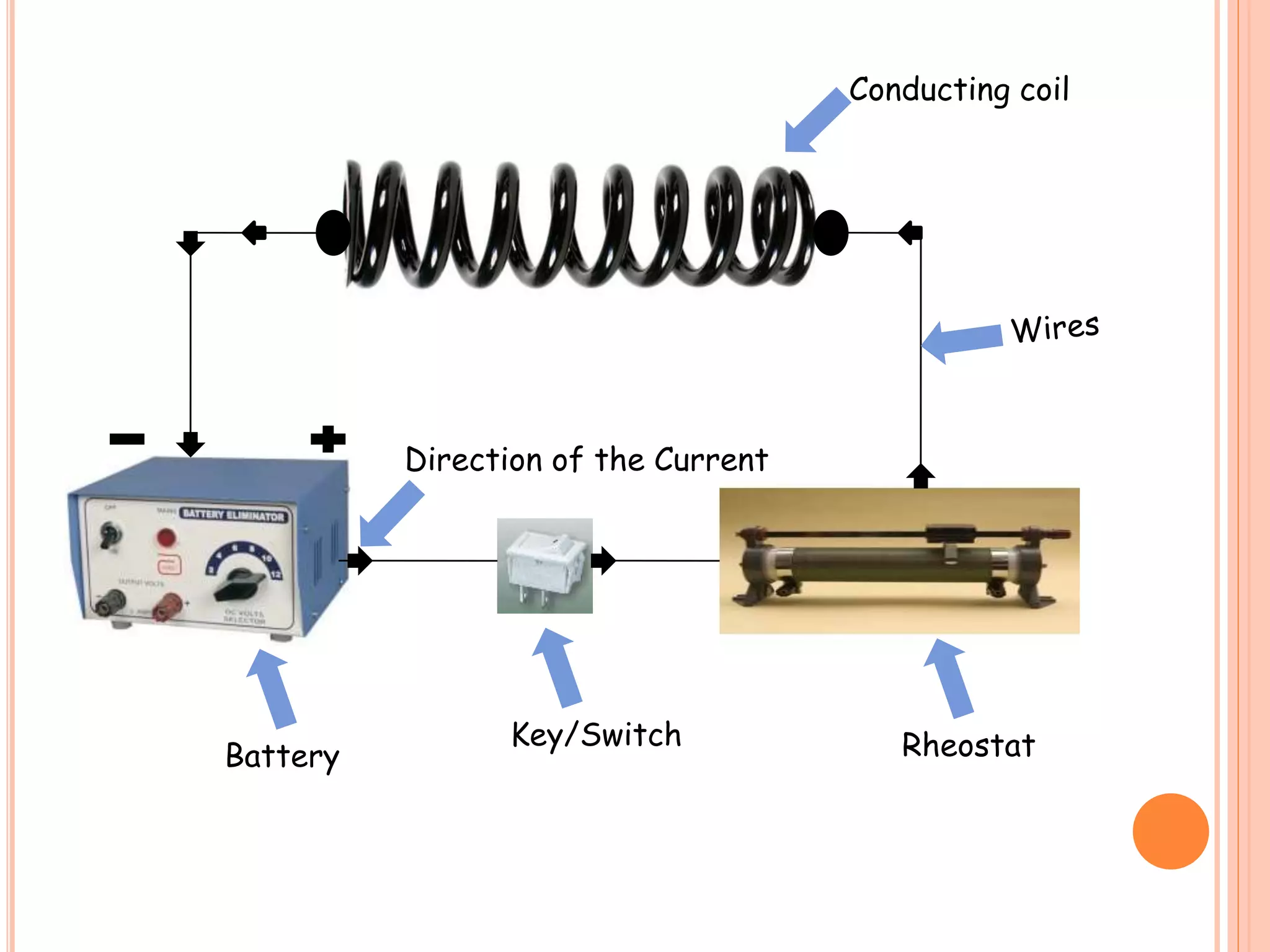
When a current passes through an insulated coil, it produces a magnetic field and links flux within the coil. This causes self-induction, where changing the current induces an electromotive force (emf) back in the coil. The self-inductance (L) of a coil depends on its shape, number of turns, and the material inside. It represents the flux linked per unit of current and does not depend on the current itself. Lenz's law applies, so the induced self emf opposes the change that created it.

1. SELF
INDUCTANCE

2. •When an electric current is passed
through an insulated conducting coil, it
gives rise to a magnetic field in the coil
so that the coil itself behaves like a
magnet.
•The magnetic flux produced by the
current in the coil is linked with the coil
itself.

3. DEFINATION
As the strength of the current in the
coil is changed, the flux linked with the coil
also changes. Under such circumstances an
emf is induced in the coil too. Such emf is
called a self-induced emf and this
phenomenon
is known as self-induction.

4. Conducting coil
Battery
Direction of the Current
Key/Switch Rheostat

5. Current flows
In anti-clock
Wise direction
Current
flows
In clock
Wise
direction

6. If the number of turn in a coil is N and
the flux linked with each turn is φ, then
the total flux linked through the coil =
Nφ.
In this case, the total flux linked with
the coil (which is called flux linkage) is
directly proportional to the current I
flowing through the coil.

7. N = LI
where the constant of proportionality
L is called the self-inductance of a coil.
N = LI, L= N/I
The self inductance L is a measure of
the flux linked with coil per unit
current.

8. •The self-inductance L of a coil depends
upon –
(1)The size and shape of the coil.
(2) The number of turns N.
(3) The magnetic property of the medium
within the coil in which the flux exists.
NOTE:Self-inductance L does not depend
on current I.

9. Diffrentiating equation N = LI with
respect to time t,
N d/dt = L dI/dt
In the case of self-induction, Faraday’s
law and Lenz’s law holds good. Hence self-induced
emf in the coil is,
e = -N d/dt
Self-induced emf is also called “back
emf”.

10. Form equation e = -L dI/dt
Self inductance L = -e/(dI/dt)
“The self-induced emf produced per unit
rate of change of current in the circuits
called self-inductance of the circuit.”
Unit of L =unit of emf(v)/Unit of rate
of change of current (A/s)=Vs/A or
Henry(H)