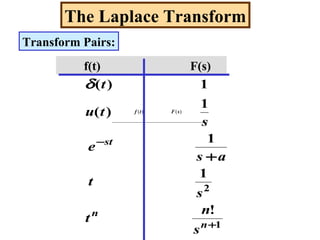
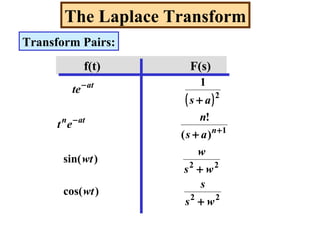
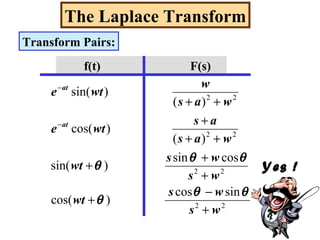
The document provides an overview of the Laplace transform including: - Definitions of the Laplace transform and inverse Laplace transform - Transform pairs for common functions like unit step, unit impulse, exponentials, sinusoids - Properties for time shifting, frequency shifting, differentiation, integration - Theorems for finding the initial value and final value of a function from its Laplace transform - Examples of using the Laplace transform and its properties

1. The Laplace Transform
The University of Tennessee
Electrical and Computer Engineering Department
Knoxville, Tennessee
wlg

2. The Laplace Transform
The Laplace Transform of a function, f(t), is defined as;
∫
∞
−
==
0
)()()]([ dtetfsFtfL st
The Inverse Laplace Transform is defined by
∫
∞+
∞−
−
==
j
j
ts
dsesF
j
tfsFL
σ
σ
π
)(
2
1
)()]([1
*notes
Eq A
Eq B

3. The Laplace Transform
We generally do not use Eq B to take the inverse Laplace. However,
this is the formal way that one would take the inverse. To use
Eq B requires a background in the use of complex variables and
the theory of residues. Fortunately, we can accomplish the same
goal (that of taking the inverse Laplace) by using partial fraction
expansion and recognizing transform pairs.
*notes

4. The Laplace Transform
Laplace Transform of the unit step.
*notes
|0
0
1
1)]([
∞−
∞
−
∫
−
== stst
e
s
dtetuL
s
tuL
1
)]([ =
The Laplace Transform of a unit step is:
s
1

5. The Laplace Transform
The Laplace transform of a unit impulse:
Pictorially, the unit impulse appears as follows:
0 t0
f(t) δ(t – t0)
Mathematically:
δ(t – t0) = 0 t ≠ 0
*note
01)(
0
0
0 >=−∫
+
−
εδ
ε
ε
dttt
t
t

6. The Laplace Transform
The Laplace transform of a unit impulse:
An important property of the unit impulse is a sifting
or sampling property. The following is an important.
∫ 


><
<<
=−
2
1
2010
2010
0
,0
)(
)()(
t
t
tttt
ttttf
dttttf δ

7. The Laplace Transform
The Laplace transform of a unit impulse:
In particular, if we let f(t) = δ(t) and take the Laplace
1)()]([ 0
0
=== −−
∞
∫
sst
edtettL δδ

8. The Laplace Transform
An important point to remember:
)()( sFtf ⇔
The above is a statement that f(t) and F(s) are
transform pairs. What this means is that for
each f(t) there is a unique F(s) and for each F(s)
there is a unique f(t). If we can remember the
Pair relationships between approximately 10 of the
Laplace transform pairs we can go a long way.

9. The Laplace Transform
Building transform pairs:
eL(
∫∫
∞
+−
∞
−−−
==
e
tasstatat
dtedteetueL
0
)(
0
)]([
asas
e
tueL
st
at
+
=
+
−
=
∞−
−
1
)(
)]([ |0
as
tue at
+
⇔− 1
)(A transform
pair

10. The Laplace Transform
Building transform pairs:
∫
∞
−
=
0
)]([ dttettuL st
∫ ∫
∞ ∞
∞
−=
0 0
0
| vduuvudv
u = t
dv = e-st
dt
2
1
)(
s
ttu ⇔
A transform
pair

11. The Laplace Transform
Building transform pairs:
22
0
11
2
1
2
)(
)][cos(
ws
s
jwsjws
dte
ee
wtL st
jwtjwt
+
=






+
−
−
=
+
= −
∞ −
∫
22
)()cos(
ws
s
tuwt
+
⇔ A transform
pair

12. The Laplace Transform
Time Shift
∫ ∫
∫
∞ ∞
−−+−
∞
−
=
∞→∞→→→
+==−=
−=−−
0 0
)(
)()(
,.,0,
,
)()]()([
dxexfedxexf
SoxtasandxatAs
axtanddtdxthenatxLet
eatfatuatfL
sxasaxs
a
st
)()]()([ sFeatuatfL as−
=−−

13. The Laplace Transform
Frequency Shift
∫
∫
∞
+−
∞
−−−
+==
=
0
)(
0
)()(
)]([)]([
asFdtetf
dtetfetfeL
tas
statat
)()]([ asFtfeL at
+=−

14. The Laplace Transform
Example: Using Frequency Shift
Find the L[e-at
cos(wt)]
In this case, f(t) = cos(wt) so,
22
22
)(
)(
)(
)(
was
as
asFand
ws
s
sF
++
+
=+
+
=
22
)()(
)(
)]cos([
was
as
wteL at
++
+
=−

15. The Laplace Transform
Time Integration:
The property is:
stst
t
st
t
e
s
vdtedv
and
dttfdudxxfuLet
partsbyIntegrate
dtedxxfdttfL
−−
−
∞∞
−==
==






=





∫
∫ ∫∫
1
,
)(,)(
:
)()(
0
0 00

16. The Laplace Transform
Time Integration:
Making these substitutions and carrying out
The integration shows that
)(
1
)(
1
)(
00
sF
s
dtetf
s
dttfL st
=
=





∫∫
∞
−
∞

17. The Laplace Transform
Time Differentiation:
If the L[f(t)] = F(s), we want to show:
)0()(]
)(
[ fssF
dt
tdf
L −=
Integrate by parts:
)(),(
)(
,
tfvsotdfdt
dt
tdf
dv
anddtsedueu stst
===
−== −−
*note

18. The Laplace Transform
Time Differentiation:
Making the previous substitutions gives,
[ ]
∫
∫
∞
−
∞
−∞−
+−=
−−=





0
0
0
)()0(0
)()( |
dtetfsf
dtsetfetf
dt
df
L
st
stst
So we have shown:
)0()(
)(
fssF
dt
tdf
L −=




19. The Laplace Transform
Time Differentiation:
We can extend the previous to show;
)0(...
)0(')0()(
)(
)0('')0(')0()(
)(
)0(')0()(
)(
)1(
21
23
3
3
2
2
2
−
−−
−−
−−=





−−−=





−−=





n
nnn
n
n
f
fsfssFs
dt
tdf
L
casegeneral
fsffssFs
dt
tdf
L
fsfsFs
dt
tdf
L

20. The Laplace Transform
Transform Pairs:
____________________________________
)()( sFtf
f(t) F(s)
1
2
!
1
1
1
)(
1)(
+
−
+
n
n
st
s
n
t
s
t
as
e
s
tu
tδ

21. The Laplace Transform
Transform Pairs:
f(t) F(s)
( )
22
22
1
2
)cos(
)sin(
)(
!
1
ws
s
wt
ws
w
wt
as
n
et
as
te
n
atn
at
+
+
+
+
+
−
−

22. The Laplace Transform
Transform Pairs:
f(t) F(s)
22
22
22
22
sincos
)cos(
cossin
)sin(
)(
)cos(
)(
)sin(
ws
ws
wt
ws
ws
wt
was
as
wte
was
w
wte
at
at
+
−
+
+
+
+
++
+
++
−
−
θθ
θ
θθ
θ Yes !

23. The Laplace Transform
Common Transform Properties:
f(t) F(s)
)(
1
)(
)(
)(
)0(...)0(')0()(
)(
)()(
)([0),()(
)(0),()(
0
1021
00
000
sF
s
df
ds
sdF
ttf
ffsfsfssFs
dt
tfd
asFtfe
ttfLetttutf
sFetttuttf
t
nnnn
n
n
at
sot
sot
∫
−
−−−−
+
+≥−
≥−−
−−−
−
−
−
λλ

24. The Laplace Transform
Using Matlab with Laplace transform:
Example Use Matlab to find the transform of t
te 4−
The following is written in italic to indicate Matlab code
syms t,s
laplace(t*exp(-4*t),t,s)
ans =
1/(s+4)^2

25. The Laplace Transform
Using Matlab with Laplace transform:
Example Use Matlab to find the inverse transform of
19.12.
)186)(3(
)6(
)( 2
prob
sss
ss
sF
+++
+
=
syms s t
ilaplace(s*(s+6)/((s+3)*(s^2+6*s+18)))
ans =
-exp(-3*t)+2*exp(-3*t)*cos(3*t)

26. The Laplace Transform
Theorem: Initial Value
If the function f(t) and its first derivative are Laplace transformable and f(t)
Has the Laplace transform F(s), and the exists, then)(lim ssF
0
)0()(lim)(lim
→∞→
==
ts
ftfssF
The utility of this theorem lies in not having to take the inverse of F(s)
in order to find out the initial condition in the time domain. This is
particularly useful in circuits and systems.
Theorem:
∞→s
Initial Value
Theorem

27. The Laplace Transform
Initial ValueTheorem:Example:
Given;
22
5)1(
)2(
)(
++
+
=
s
s
sF
Find f(0)
1
)26(2
2
lim
2512
2
lim
5)1(
)2(
lim)(lim)0(
2222
222
2
2
22
=
++
+
=








+++
+
=
++
+
==
sssss
ssss
ss
ss
s
s
sssFf
∞→s∞→s ∞→s
∞→s

28. The Laplace Transform
Theorem: Final Value Theorem:
If the function f(t) and its first derivative are Laplace transformable and f(t)
has the Laplace transform F(s), and the exists, then)(lim ssF
∞→s
)()(lim)(lim ∞== ftfssF
0→s ∞→t
Again, the utility of this theorem lies in not having to take the inverse
of F(s) in order to find out the final value of f(t) in the time domain.
This is particularly useful in circuits and systems.
Final Value
Theorem

29. The Laplace Transform
Final Value Theorem:Example:
Given:
[ ] ttesFnote
s
s
sF t
3cos)(
3)2(
3)2(
)( 21
22
22
−
=
++
−+
= −
Find )(∞f .
[ ] 0
3)2(
3)2(
lim)(lim)( 22
22
=
++
−+
==∞
s
s
sssFf
0→s0→s