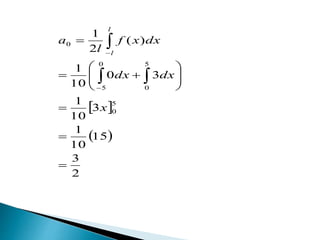1. The document defines the Fourier series as an expansion of a function in a series of sines and cosines. 2. Fourier series can be used to represent even functions as a cosine series and odd functions as a sine series. 3. Examples are provided of calculating the Fourier coefficients for different functions, including finding the Fourier series of the function f(x)=x on the interval [0,π].

1. Definition, Standard transforms & properties
By VAIBHAV TAILOR

2.  The Laplace transform of a function, f(t), is defined as
 where F(s) is the symbol for the Laplace transform, L is the
Laplace transform operator, and f(t) is some function of time,
t.




0
)()()]([ dtetfsFtf st
L

3. Sr. No Function f(t) Laplace
Transformation L(f)
1. 1
2.
3.
4.
s
1
t
n
ss
nn
nn
11
!1



at
e

1
s am
as
a
22
atsin

4. Sr. No Function f(t) Laplace
Transformation L(f)
5.
6.
7.
as
s
22

as
a
22

as
s
22

atcos
atSinh
atCosh

5.  By definition, the inverse Laplace transform operator
,L -1, converts an s-domain function back to the
corresponding time domain function
  )()(
1
tfsFL 

1
1
)1(
1
1
)1(
1
)1(
)1(
)1(
12
11
1
1
1













































e
LL
L
L
L
t
ss
ss
ss
ss
ss
s

6. No. S domain function T domain function
1
2
3
4
5
6
7
1
s a
at
e
m
as
a
22
 atsin
as
s
22
 atcos
atSinhas
a
22

atCosh
as
s
22

s
1 1
s
n
1
)!1(
1


n
t
n

7.  Linearity property
)()()]([)]([)]()([ sGsFtgLtfLtgtfL 
 ett
t
tL
523
3635


5
1
3
1
6
!2
3
!3
5
)(3)(6)(3)(5
)3()6()3()5(
21213
523
523







s
LtLLL
LtLLL
sss
ett
ett
t
t

8.   )()( asFtfL e
at

 )cos(wtL e
st
22
22
)(
)(
)(
)(
)cos()(
was
as
asF
ws
s
sF
wttf







9. )()]([ sFttfL ds
d

 
 
 
 
)(
)(
(
22
2
sin
22
)
sin
sin
)(
)()]([)(
sin)(
sin
2
2
2222
22
22
as
as
asas
as
as
as
attL
ds
daa
ds
d
attL
a
ds
d
attL
a
sF
SinatLtFLsF
attf
attL























10.   


s
t
tf
dssFL )()(
 
 
s
as
t
L
as
s
t
L
t
L
t
L
ds
asst
L
ass
sF
tfLsF
t
L
e
e
as
se
asse
e
e
e
at
at
s
at
s
at
s
at
at
at









 










 









 









 










 











 
















log
1
log1log
1
1
1
111
11
)(
1)()(
1
log
)log(log

11. Example
  )(*)()()()()(
)()]([&)()]([&
G(s)L[g(t)]&F(s)L[f(t)]If
0
1
11-
L
tgtfduutgufsGsF
tgsGtfsF
t
L
L






 
 
attgattf
sG
s
sF
ss
sGsF
s
a
asas
asasas
as
L
sin)(&cos)(
1
)(&)(
1
22
)()(
22
1
2222
22222
2
1





















12. a
att
as
s
att
as
s
a
atau
as
s
duatauat
as
s
duauauat
as
s
utautgauuf
L
L
uatL
L
L
a
t
a
t
a
t
a
a
2
sin
)22(
]sin[
)22(
2
)2(
)22(
)]2sin([sin
)22(
))}(cos{sin(2
)22(
)(sin)(&cos)(
2
2
2
2
2
1
2
11
0
2
11
0
2
11
0
2
11
1
}]cos{)([sin


























13. Definition, formula, odd & even function,
Half range series & some example

14.  A Fourier series may be defined as an expansion of a
function in a series of sines and cosines such as ,
 Henceforth we assume f satisfies the following
(Dirichlet) conditions:
1. f(x) is a periodic function;
2. f(x) has only a finite number of finite
discontinuities;
3. f(x) has only a finite number of extrem values,
maxima and minima in the interval [0,2p].
)sincos(
2
)(
0
0
nxnxxf ba
a
n
n
n
 



15. The formula for a Fourier series is
We have formulae for the coefficients (for the
derivations see the course notes):






















n
n
nn
l
xn
b
l
xn
aaxf
1
0 sincos)(



l
l
dxxf
l
a )(
2
1
0 







l
l
n dx
l
xn
xf
l
a

cos)(
1








l
l
n dx
l
xn
xf
l
b

sin)(
1

16.  Even Functions
◦ The value of the
function would be the
same when we walk
equal distances along
the X-axis in opposite
directions.
 Mathematically
speaking
q
f(q
   xfxf 

17.  Odd Functions
◦ The value of the function
would change its sign but
with the same magnitude
when we walk equal
distances along the X-
axis in opposite
directions.
 Mathematically speaking -
   xfxf 
q
f(q

18.  The Fourier series of an even function
is expressed in terms of a cosine series.
 The Fourier series of an odd function
is expressed in terms of a sine series.
 xf
  



1
0 cos
n
n nxaaxf
 xf
  



1
sin
n
n nxbxf
0bn
0ao
0an

19. Fourier
coeffici
ents
function
even
function
odd
function
neither
0a
na
nb


l
l
dxxf
l
a )(
1
0








l
l
n dx
l
xn
xf
l
a

cos)(
1








l
l
n dx
l
xn
xf
l
a

cos)(
2


l
l
dxxf
l
a )(
2
1
0








l
l
n dx
l
xn
xf
l
b

sin)(
2








l
l
n dx
l
xn
xf
l
b

sin)(
1
0
0
0

20.  Find the fourier series of f(x)=x in interval
 Solution
 The fourier series of f(x)with period is given by
)2,0( 
2
2
)1....(..........sincos)(
1
0 





















n
n
nn
l
xn
b
l
xn
aaxf









2
0
2
0
2
1
)(
2
1
xdx
dxxfa
o

21. 























22
1
22
1
4
2
2
0
2
x
 
 
0
0coscos1
cos
1
sin1
cos
1
cos)(
1
22
2
0
2
2
0
0

































 











nn
n
n
nx
n
nx
x
nxdxx
dxnxxfan









22. Put in equation 1
 
n
n
n
nx
n
nx
x
nxdxx
nxdxxfb
n
n
2
cos
2
1
sin
1
cos1
sin
1
sin)(
1
2
0
2
2
0
2
0






















































1
sin
1
2)(
n
nx
n
xf 
0a na nb

23.  Find fourier series of
 The fourier series of with period is given by
0)( xf
3
05  x
50  x
)(xf 5l
)1....(..........sincos)(
1
0 





















n
n
nn
l
xn
b
l
xn
aaxf























n
n
nn
xn
b
xn
aa
1
0
5
sin
5
cos


24.  
 
2
3
15
10
1
3
10
1
30
10
1
)(
2
1
5
0
0
5
5
0
0













 



x
dxdx
dxxf
l
a
l
l

25. 0
5
sin
5
5
3
5
cos.3
5
cos
cos.0
5
1
cos)(
1
5
0
5
0
0
5




























xn
n
dx
xn
dx
xn
dx
l
xn
xf
l
a
l
l
n





26.  
  n
l
l
n
n
n
n
xn
n
dx
xn
dx
xn
dx
l
xn
xf
l
b
11
3
0coscos
3
5
cos
5
5
3
5
sin3
5
sin.0
5
1
sin)(
1
5
0
0
5
5
0































 










  
5
sin
113
2
3
)(
1
xn
n
xf
n
n










 


27. Find the fourier series of in the
interval
is an even function
here,
The fourier series of an even function with
period is given by
xxf
2
)( 
 ,
xxf
2
)( 
0bn
2




1
0
cos)(
n
n
nxxf aa

28. 3
3
1
3
1
1
)(
1
2
3
0
3
0
2
0
0
































x
x dx
dxxfa
 
 n
n
n
n
nn
x
x
n
nxnx
x
n
nx
nxdx
nxdxxfa
1
4
cos
4
sin
2
cos
2
sin2
cos
2
cos)(
2
2
2
0
32
2
0
2
0













































  nxxf
n
n
n
cos
1
4
3
)(
1
2
2




 

29.  Find Fourier sine series of in interval
 Here, ;
 The fourier sine series of in interval
xxf )(
 x0
xxf )(  x0
l
xxf )(
),0( 
  )1......(..........sin
1




n
n nxbxf

30.  
 
   
   
  
n
n
n
con
n
nx
nx
n
nx
x
nxdxx
nxdxxf
n
bn
2
10
2
0
0
cos2
sin
1
cos2
sin
2
sin
2
0
2
0
0




























































1
sin
1
2
n
nx
n
x

31.  Find Fourier cosine series of in rang
 Here, ;
 The Fourier cosine series of in
interval is
 Where
xxf )(
 l,0
xxf )(  lx 0
xxf )(
 l,0
  



1
0 cos
n
n
l
xn
aaxf


l
dxxf
l
a
0
0 )(
2
2

32. 2
2
1
2
1
1
)(
2
2
2
0
2
0
0
0
l
l
l
xdx
l
dxxf
l
a
l
x
l
l
l























   
 
 
  11
2
0coscos
2
cos
1
sin2
cos)(
2
2
2
0
2
0















































 
n
l
l
n
n
l
n
n
l
l
n
l
l
xn
n
l
l
xn
x
l
dx
l
xn
xf
l
a








    








 

1
22
cos
112
2 n l
xn
n
ll
xf



33. Thank you