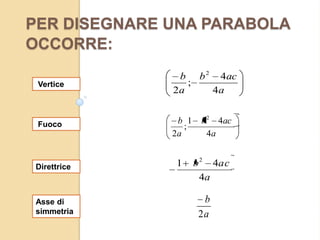
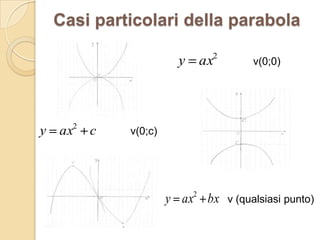
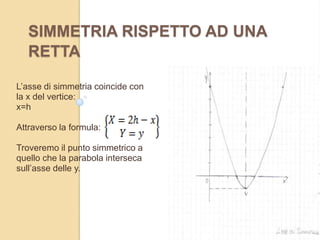
La parabola è definita come il luogo geometrico dei punti equidistanti da un fuoco e una direttrice, con l'equazione ax² + bx + c. A seconda del segno di a, la parabola è concava verso l'alto o verso il basso e può essere disegnata trovando vertice, fuoco e direttrice. Diversi metodi consentono di determinare intersezioni con gli assi e punti simmetrici, e la parabola può essere descritta con diverse informazioni come fuoco e direttrice o vertice e punti specifici.

1. La parabola

2. La parabola
L’equazione della parabola è: ax2 bx c y
La parabola è il luogo geometrico dei punti del
piano equidistanti da un punto fisso detto fuoco e
da una retta fissa detta direttrice.
a>0 parabola concava verso l’alto
a<0 concava verso il basso

3. PER DISEGNARE UNA PARABOLA
OCCORRE:
b b 2 4ac
Vertice ;
2a 4a
Fuoco b 1 b 2 4ac
;
2a 4a
Direttrice 1 b 2 4ac
4a
Asse di b
simmetria 2a

4. Quando la parabola taglia l’asse delle
x, per trovare le intersezioni con l’asse
legheremo al sistema l’equazione:
y ax2 bx c
Y=0 y 0
Quando invece taglia l’asse delle y:
y ax2 bx c
X=0 x 0

5. Casi particolari della parabola
2
y ax v(0;0)
y ax2 c v(0;c)
y ax2 bx v (qualsiasi punto)

6. SIMMETRIA RISPETTO AD UNA
RETTA
L’asse di simmetria coincide con
la x del vertice:
x=h
Attraverso la formula:
Troveremo il punto simmetrico a
quello che la parabola interseca
sull’asse delle y.

7. Parabola noti il fuoco e la
direttrice

8. Equazione della parabola noti
vertice e un punto

9. Parabola passante per tre
punti

10. Ricavare le tangenti ad una
parabola da un punto esterno

11. Fine