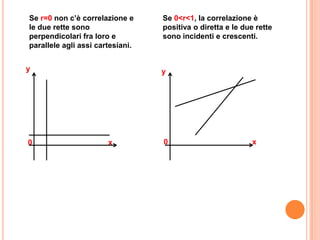
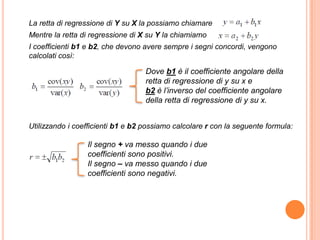
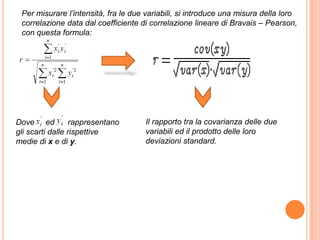
La correlazione è una relazione tra variabili, classificata come perfetta se segue un'equazione esatta o parziale se non la soddisfa completamente. Il coefficiente di correlazione varia da -1 a 1, indicando la forza e la direzione della relazione tra variabili. Lo studio della regressione utilizza la retta di regressione per esprimere matematicamente questa relazione, con il coefficiente di determinazione che misura l'aderenza del modello al fenomeno analizzato.

1. LA CORRELAZIONE

2. La correlazione è una relazione tra due o più variabili.
Una correlazione si dice perfetta se tutti i valori delle variabili soddisfano
esattamente un'equazione, ad esempio, fra il lato di un quadrato e la
sua area.
l Area = l²
La correlazione tra il lato di un quadrato e la sua area è una correlazione
perfetta.

3. Una correlazione si dice parziale quando i valori delle variabili non
soddisfano esattamente un’equazione, ad esempio, fra altezza e peso di
una persona.
La correlazione fra altezza e peso è appunto una correlazione parziale.

4. IL GRADO DI CORRELAZIONE
In statistica, si usa definire il grado di correlazione fra due variabili
attraverso un indice di correlazione che può andare da –1 a 1.
Un valore di –1 indica una correlazione perfetta negativa mentre un
valore di 1 indica una correlazione perfetta positiva.

5. LE RETTE DI REGRESSIONE AVRANNO UN
ANDAMENTO SEGUENTE:
Se r=-1, la correlazione è Se –1<r<0, la correlazione è
perfetta inversa e le due rette negativa o inversa e le due
sono coincidenti e rette sono incidenti e
decrescenti. decrescenti.
y y
0 x 0 x

6. Se r=0 non c’è correlazione e Se 0<r<1, la correlazione è
le due rette sono positiva o diretta e le due rette
perpendicolari fra loro e sono incidenti e crescenti.
parallele agli assi cartesiani.
y y
0 x 0 x

7. Se r=1, la correlazione è perfetta diretta e le due rette sono coincidenti e
crescenti.
y
0 x

8. LO STUDIO DELLA REGRESSIONE
Lo studio della regressione consiste nella determinazione di una funzione
matematica che esprime la relazione fra le variabili.
Applicando il metodo dei minimi quadrati si ottiene la retta y = a + b∙x che è
detta retta di regressione di Y rispetto ad X.

9. La retta di regressione di Y su X la possiamo chiamare
Mentre la retta di regressione di X su Y la chiamiamo
I coefficienti b1 e b2, che devono avere sempre i segni concordi, vengono
calcolati così:
Dove b1 è il coefficiente angolare della
retta di regressione di y su x e
b2 è l’inverso del coefficiente angolare
della retta di regressione di y su x.
Utilizzando i coefficienti b1 e b2 possiamo calcolare r con la seguente formula:
Il segno + va messo quando i due
coefficienti sono positivi.
Il segno – va messo quando i due
coefficienti sono negativi.

10. Per misurare l’intensità, fra le due variabili, si introduce una misura della loro
correlazione data dal coefficiente di correlazione lineare di Bravais – Pearson,
con questa formula:
Dove ed rappresentano Il rapporto tra la covarianza delle due
gli scarti dalle rispettive variabili ed il prodotto delle loro
medie di x e di y. deviazioni standard.

11. IL COEFFICIENTE DI DETERMINAZIONE
Il coefficiente di determinazione, cioè il quadrato di r, utile per valutare
la bontà di un modello di regressione, indica la percentuale di
variabilità totale dovuta alla dipendenza lineare della y dalla x, più r² si
avvicina a 1 più il modello rappresentato è aderente al fenomeno in
studio.

12. Presentazione
a cura di: