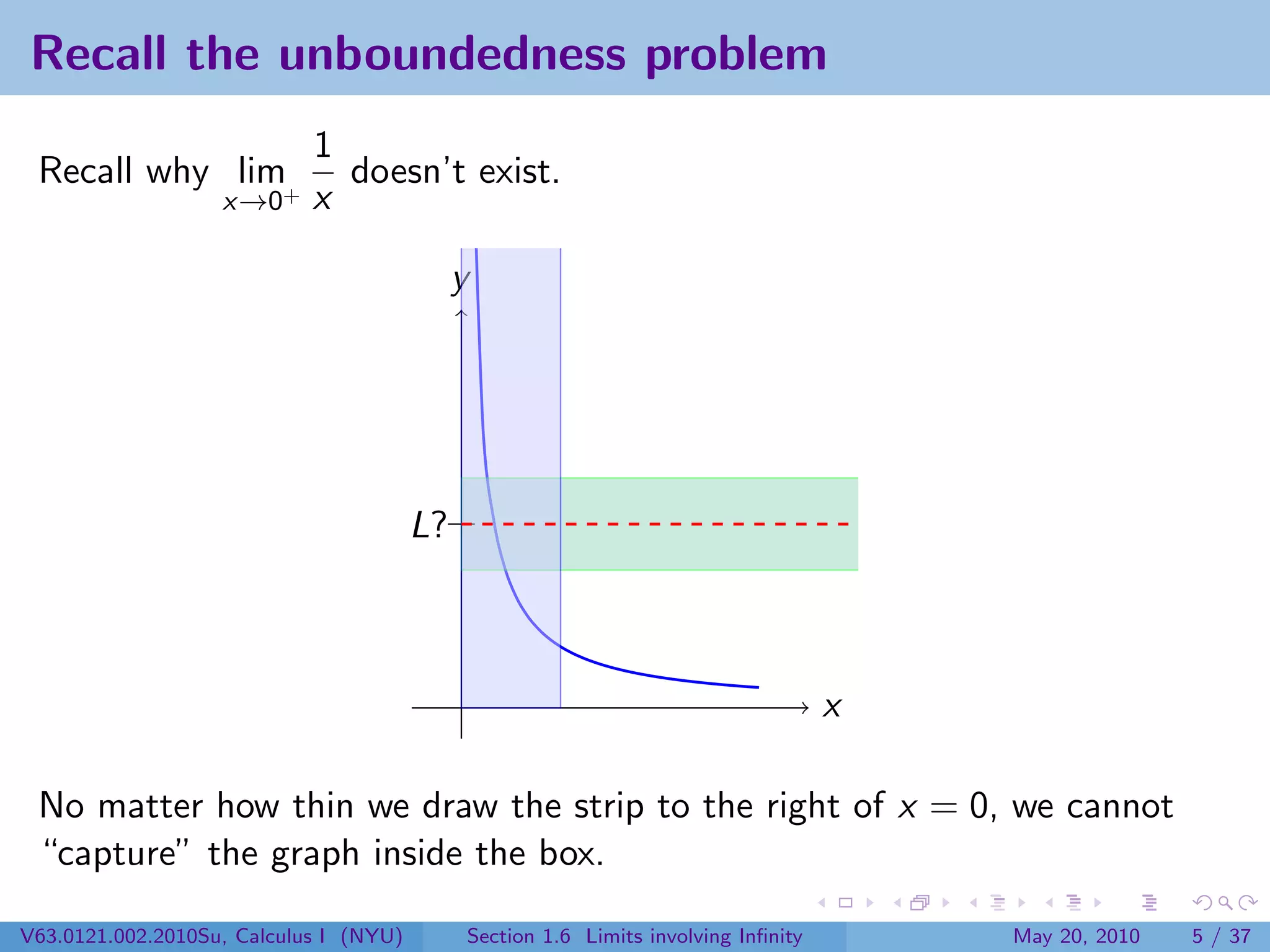
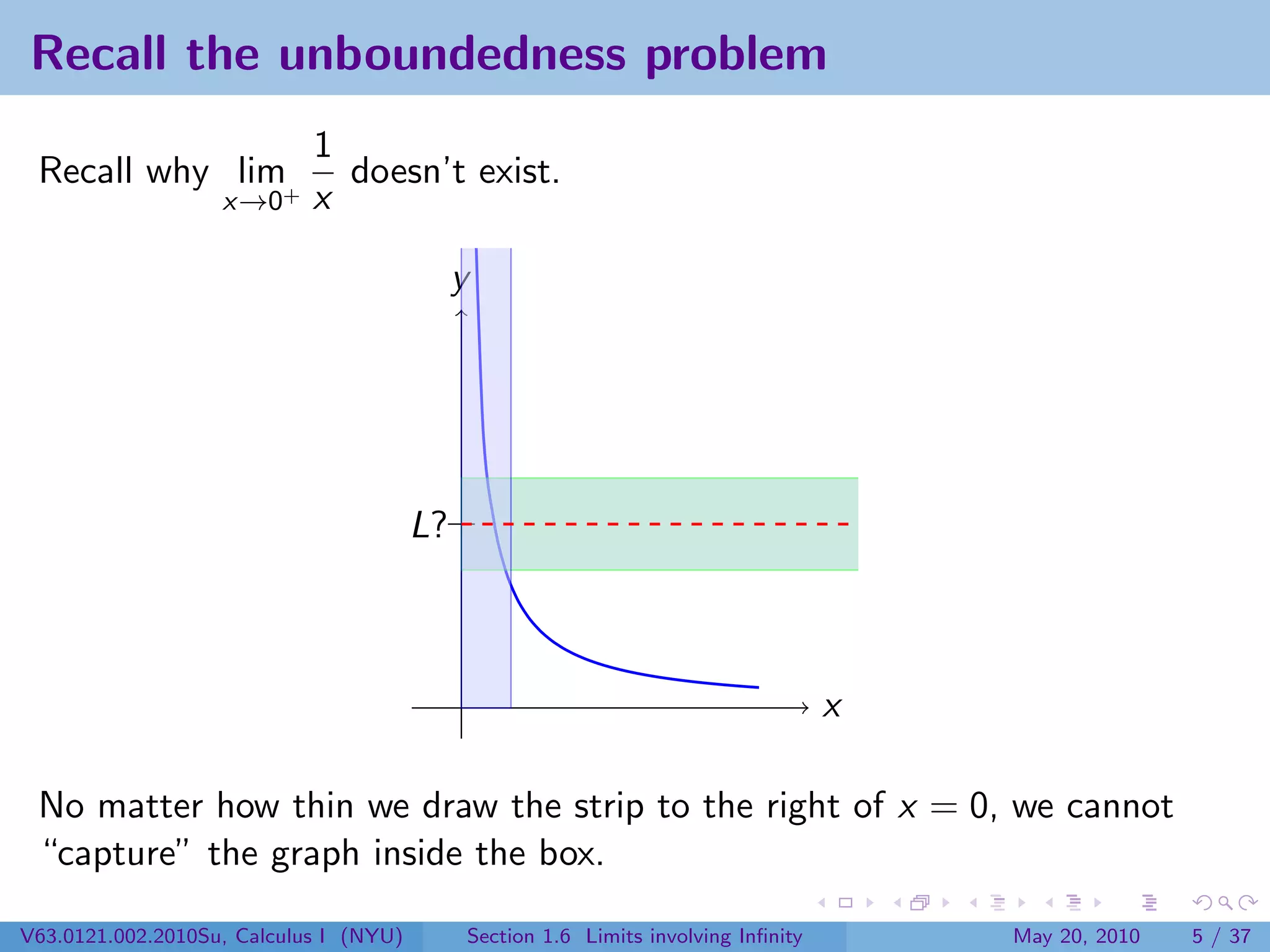
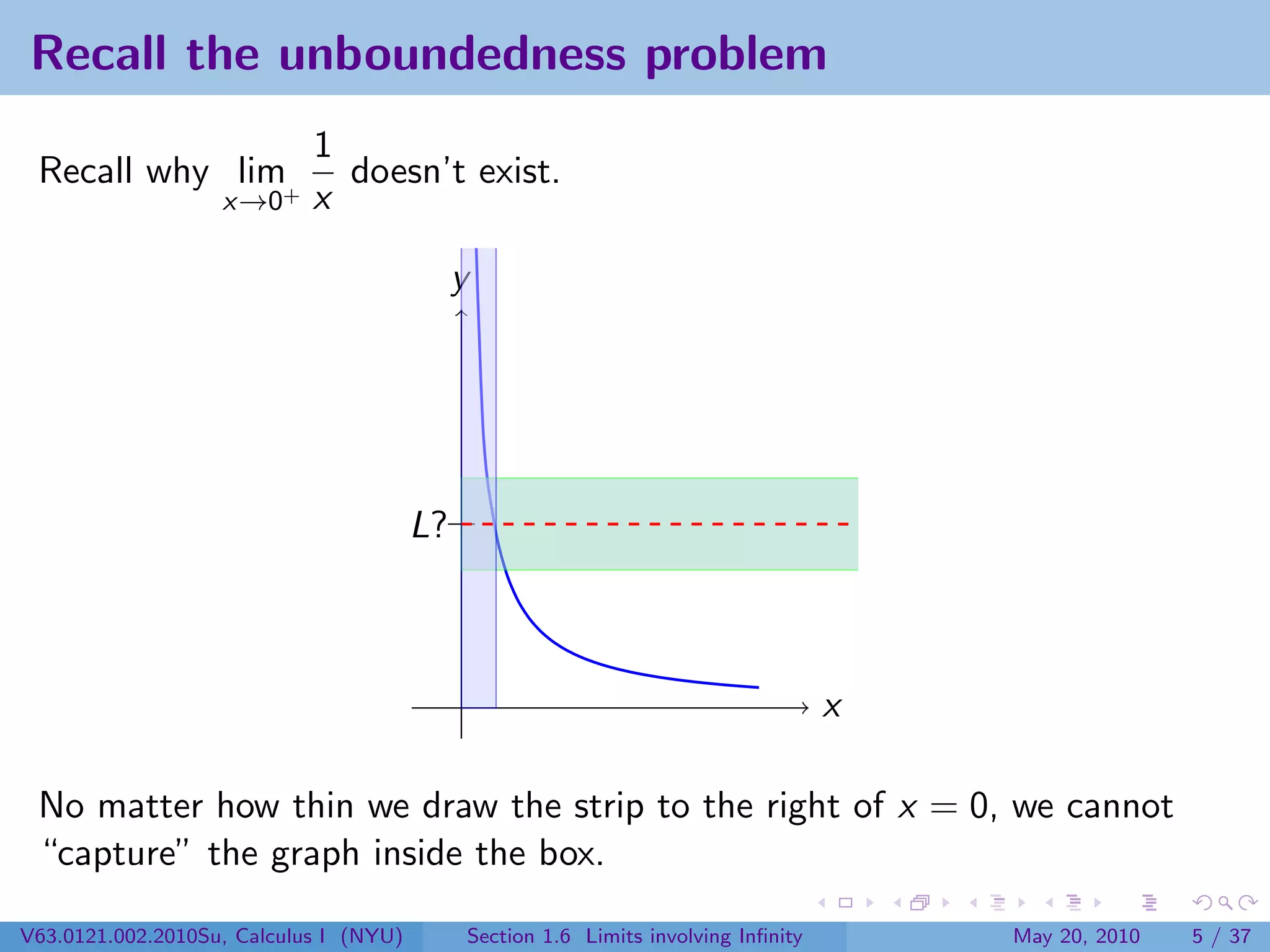
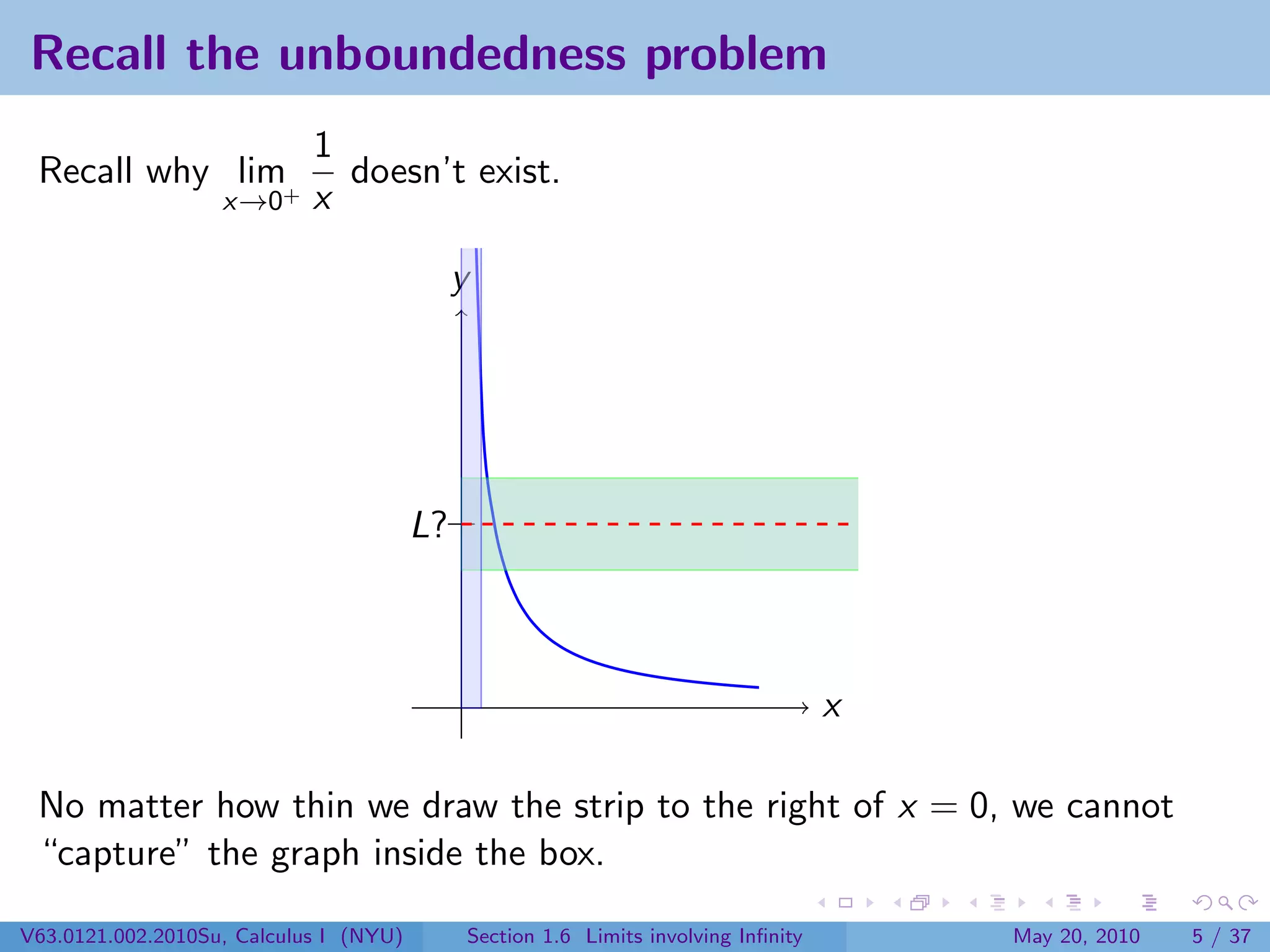
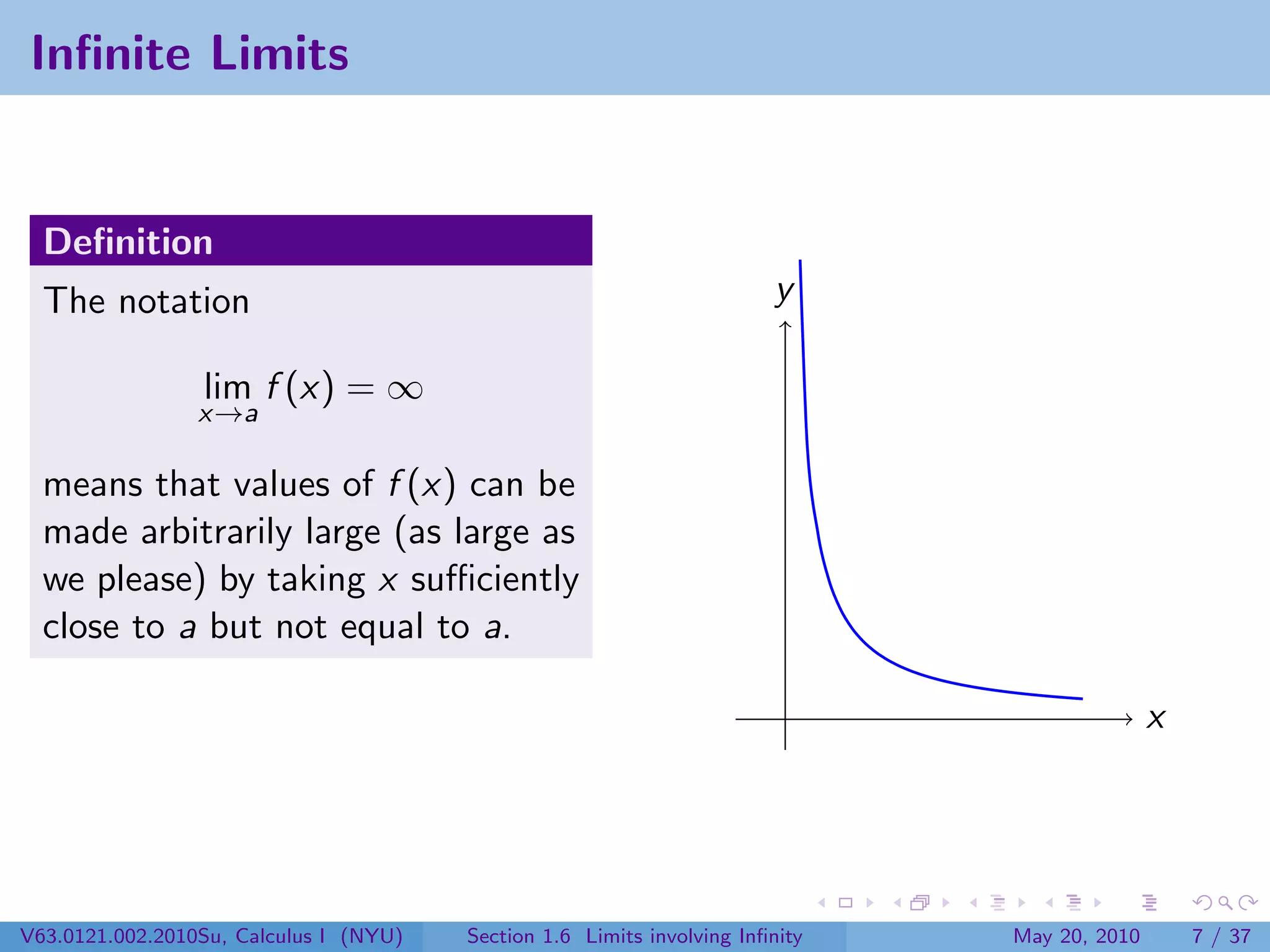
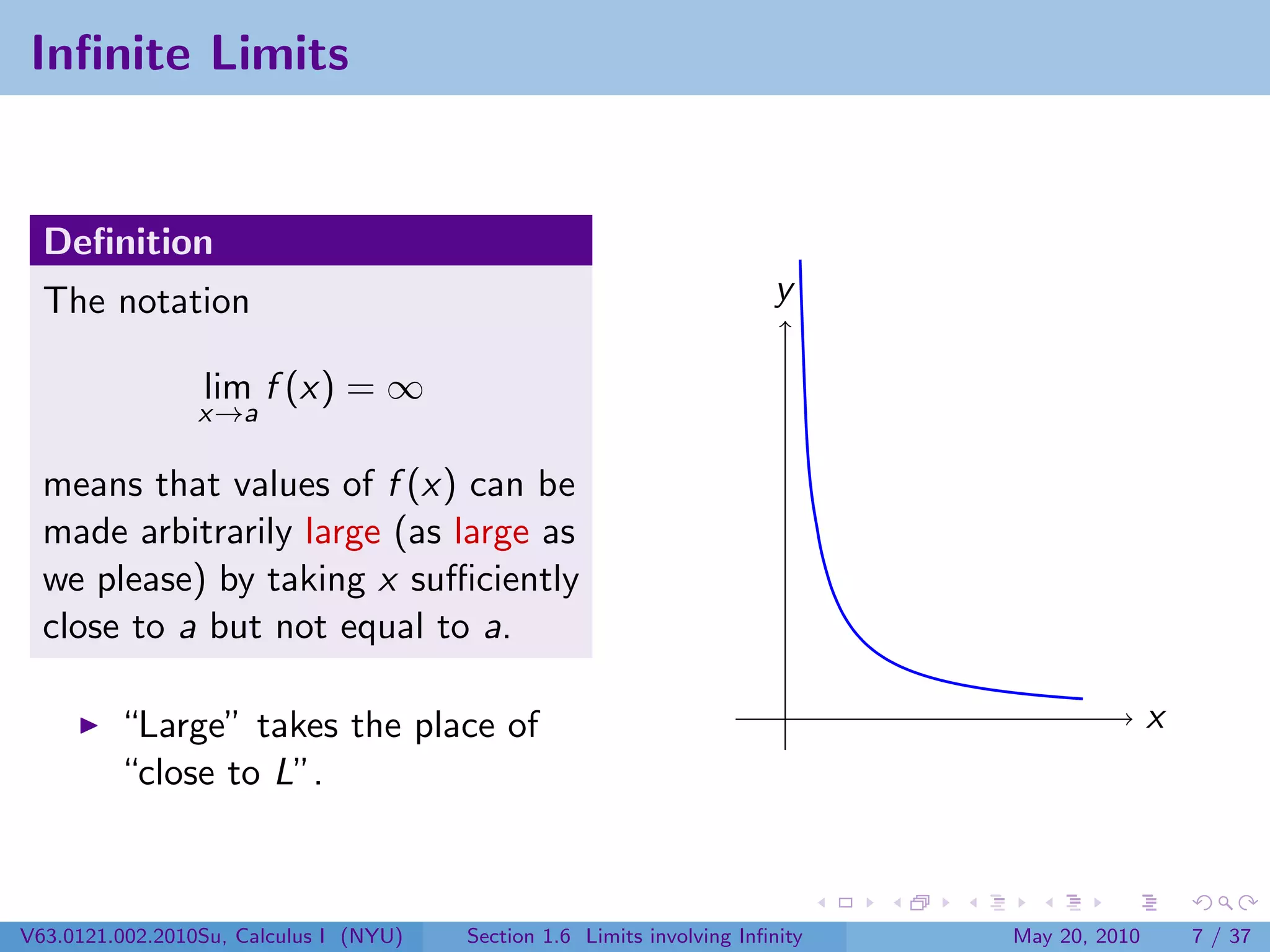
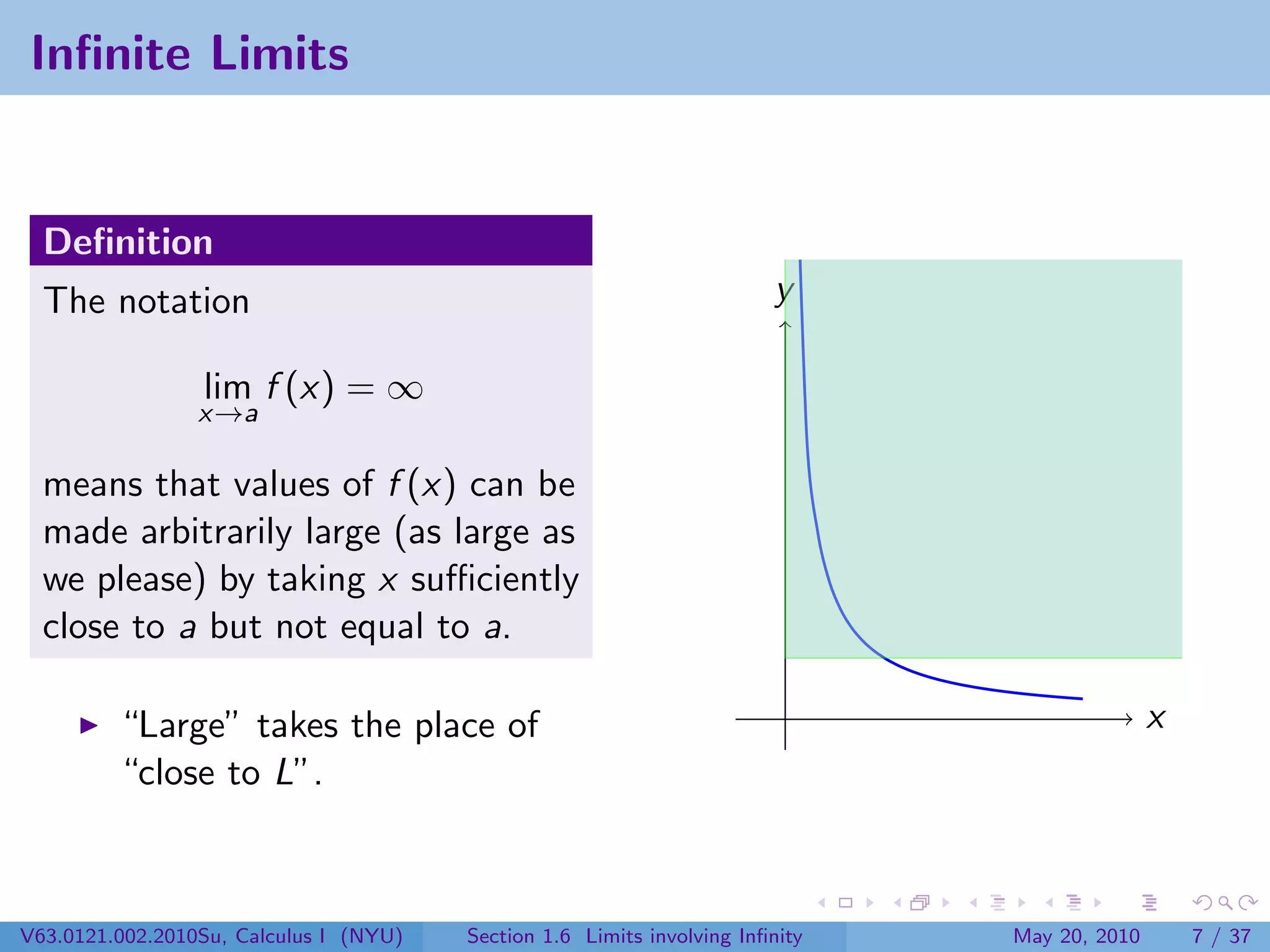
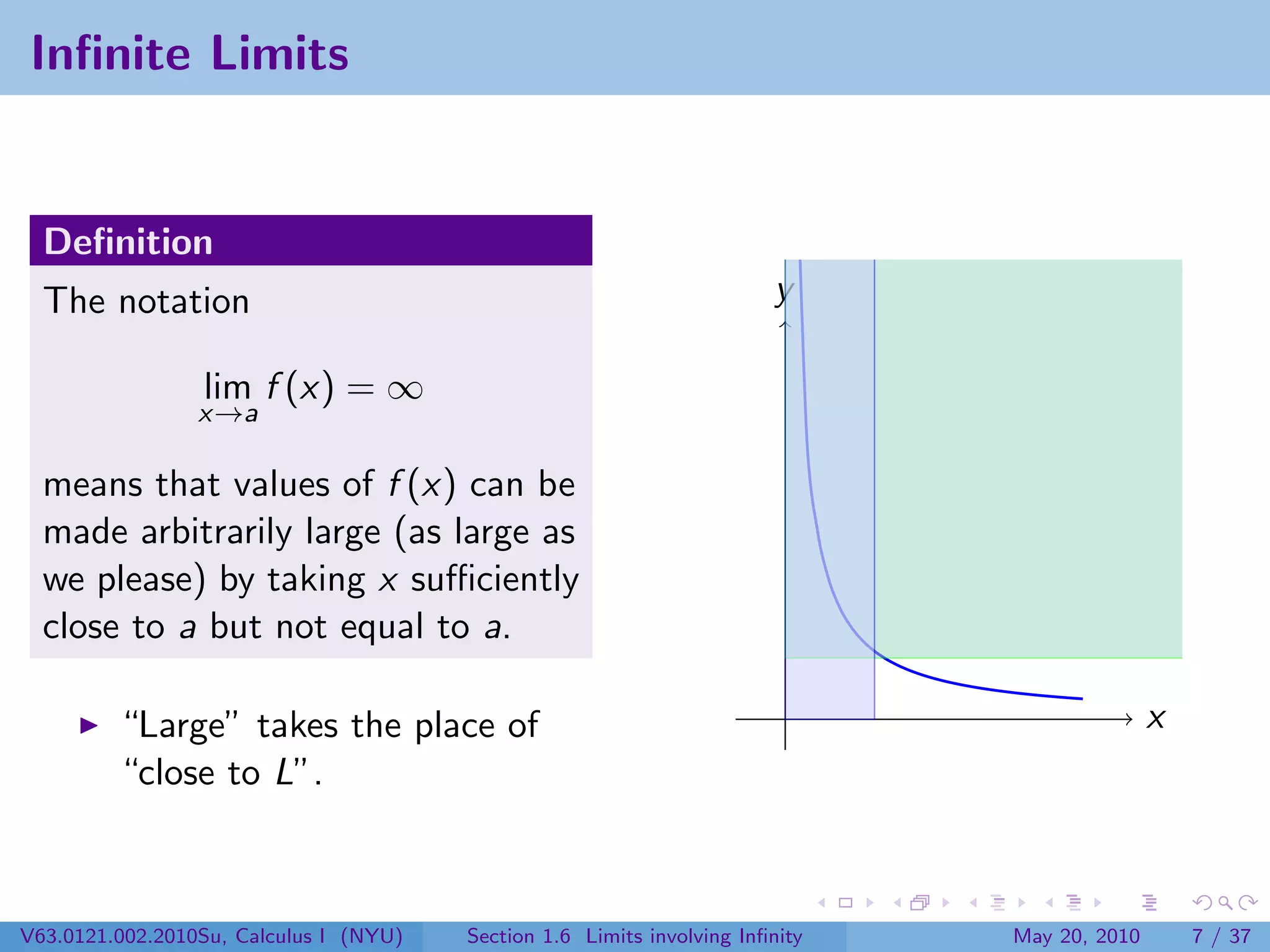
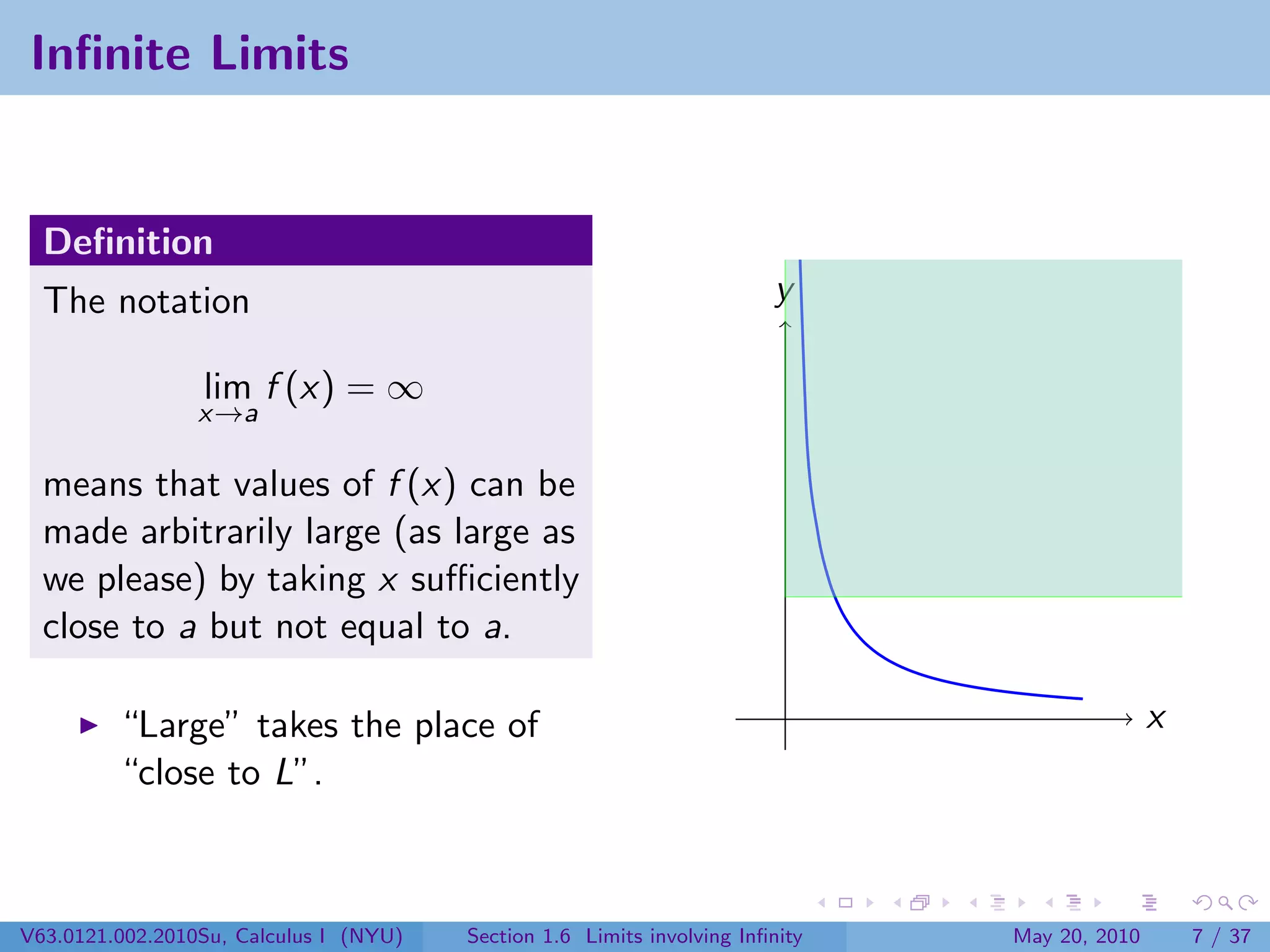
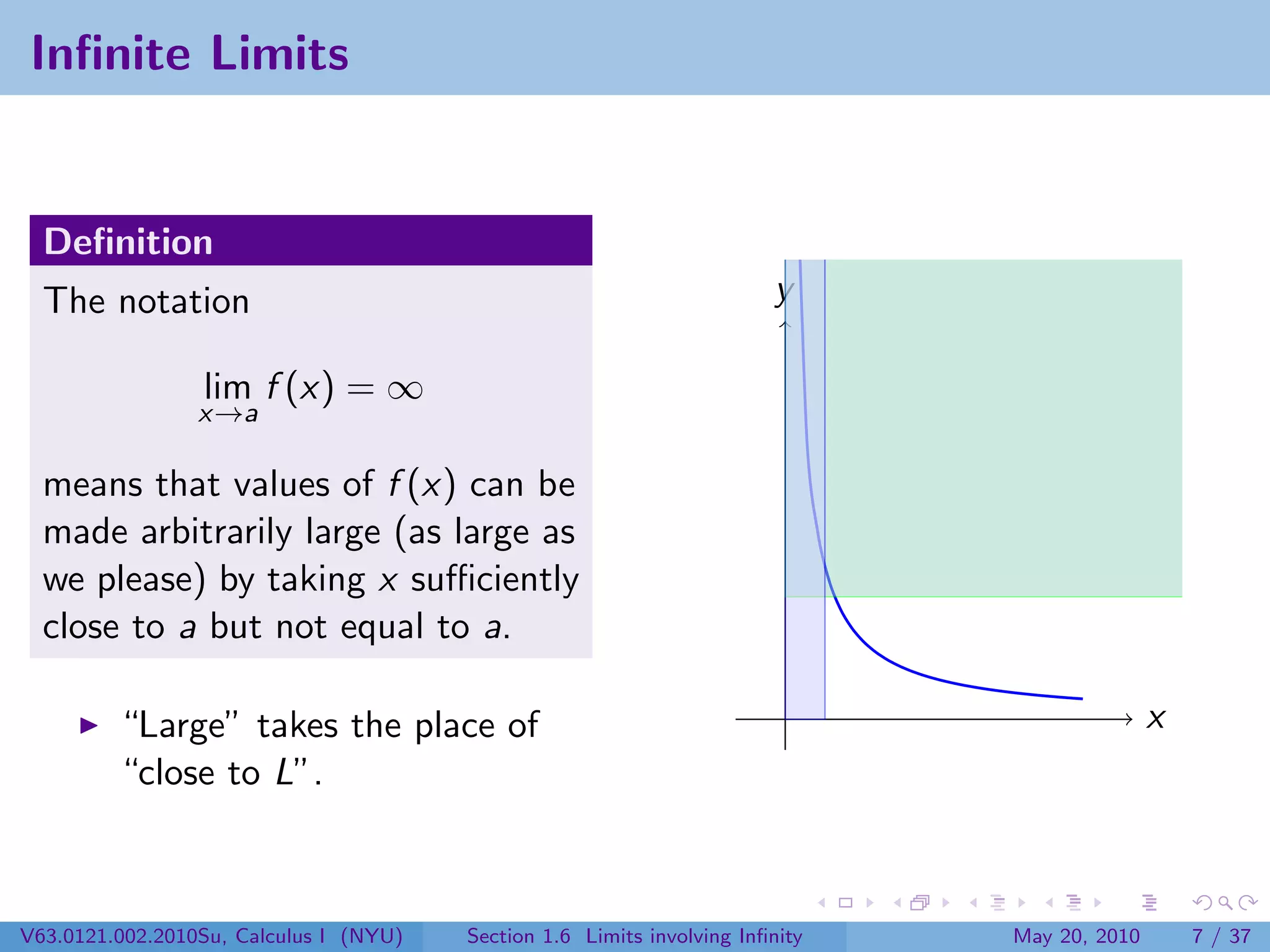
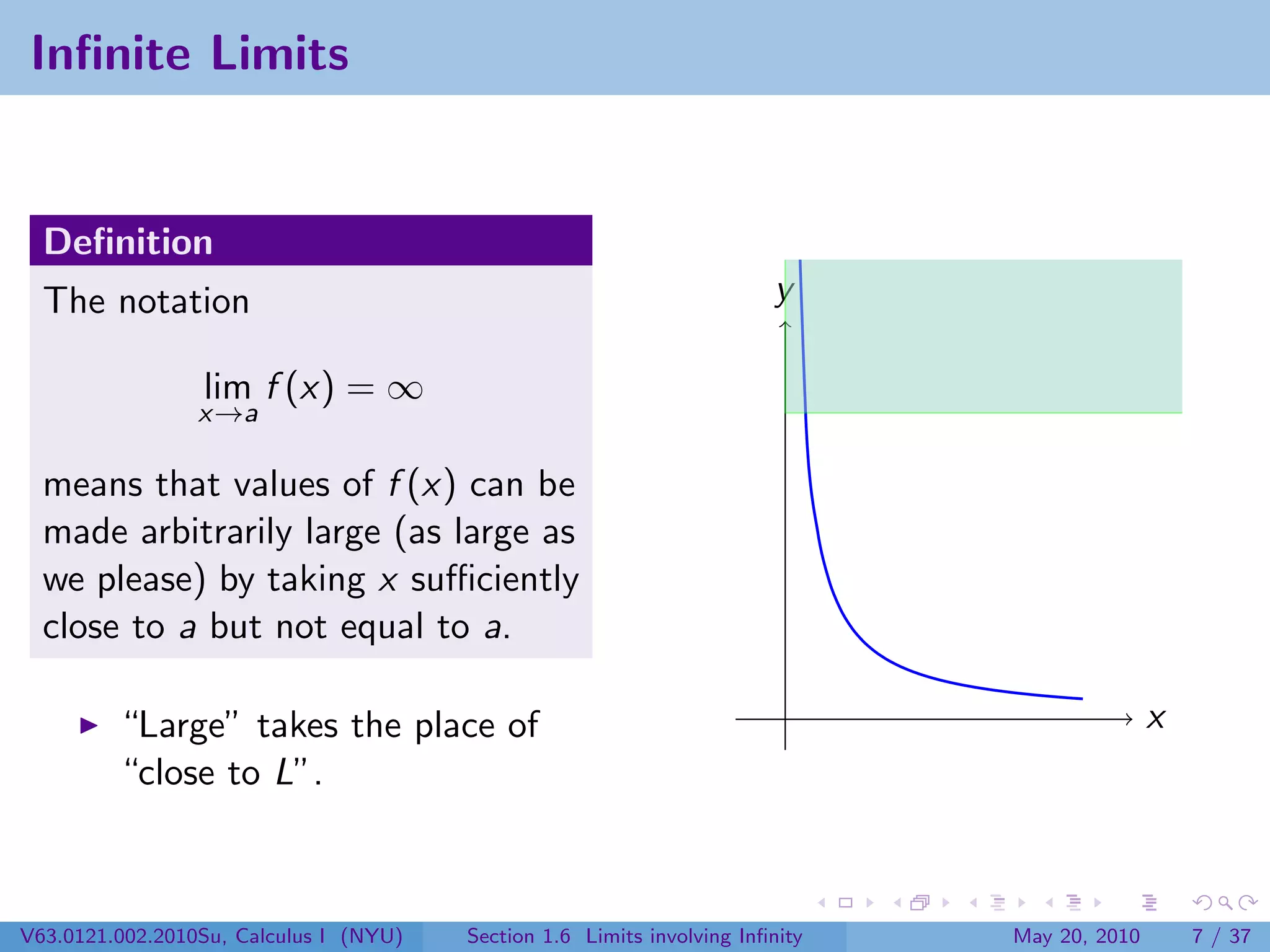
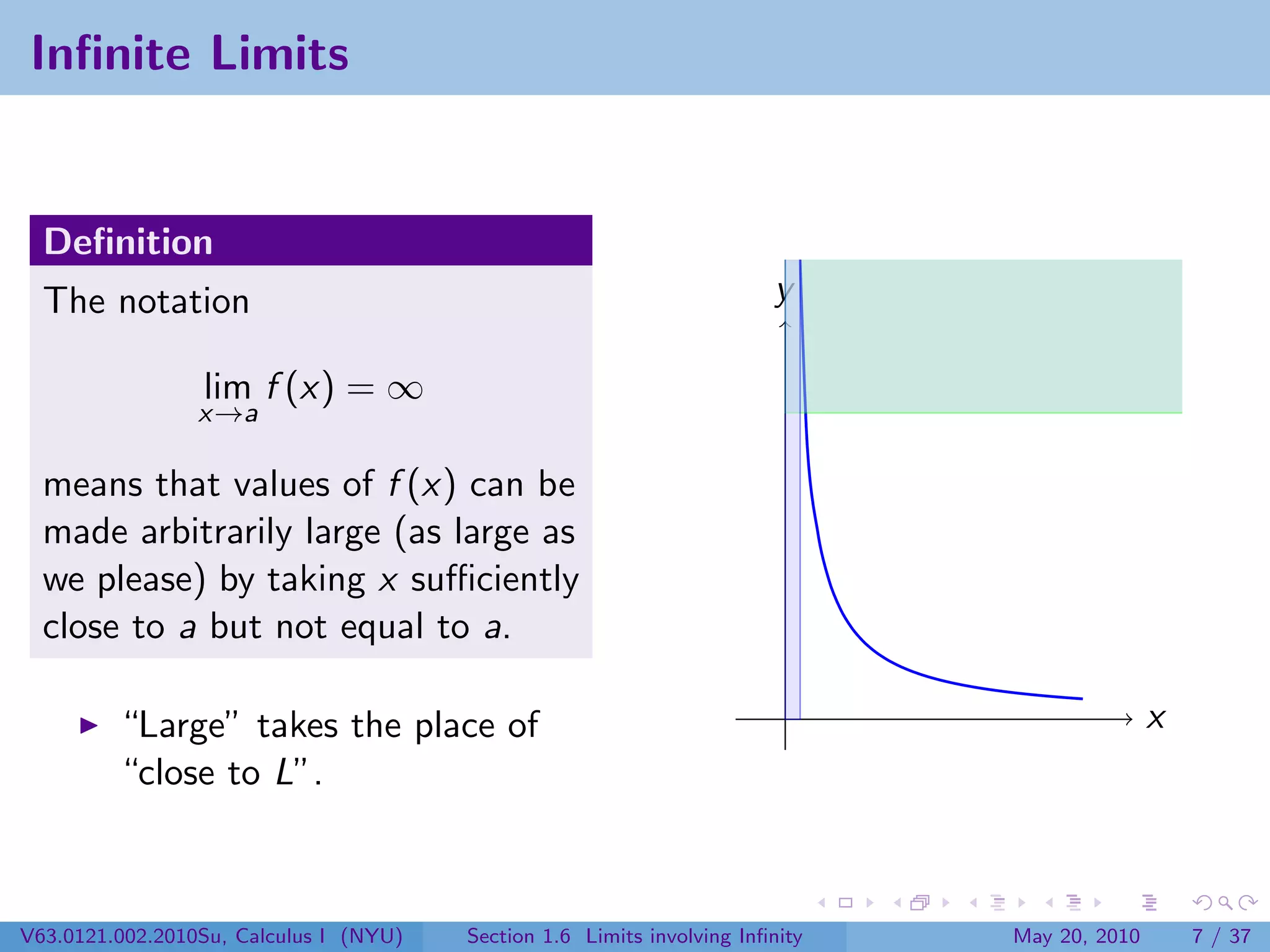
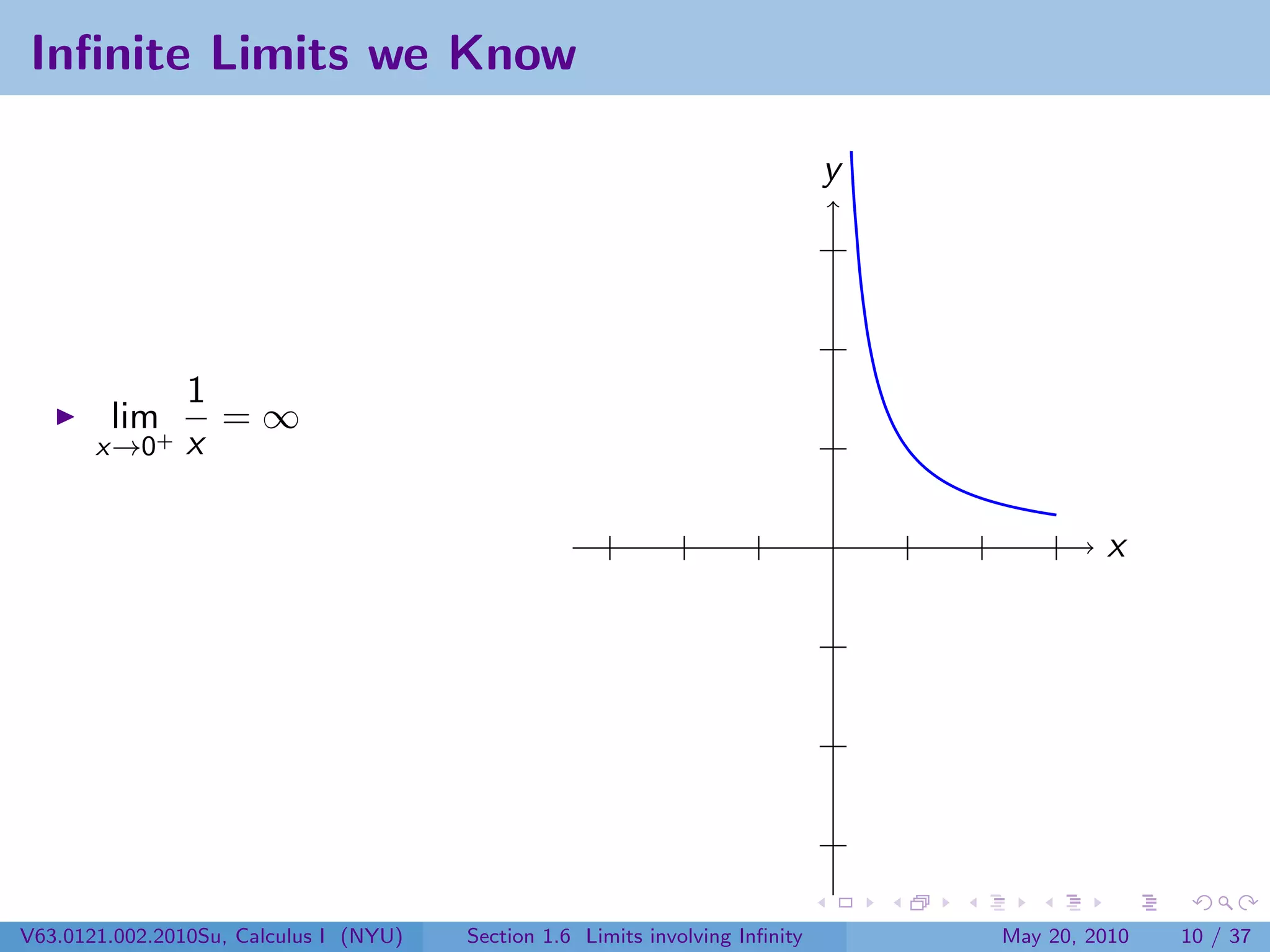
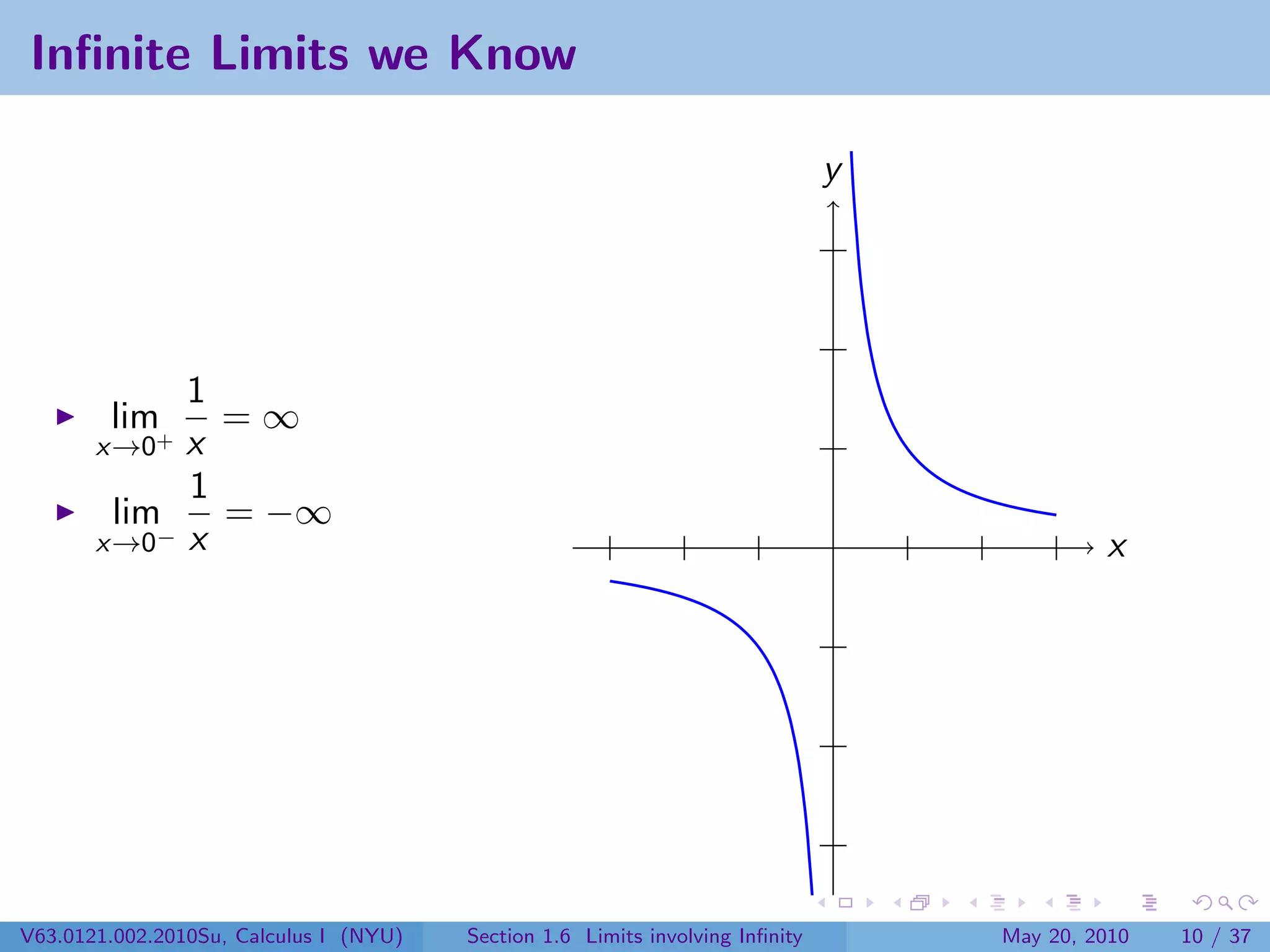
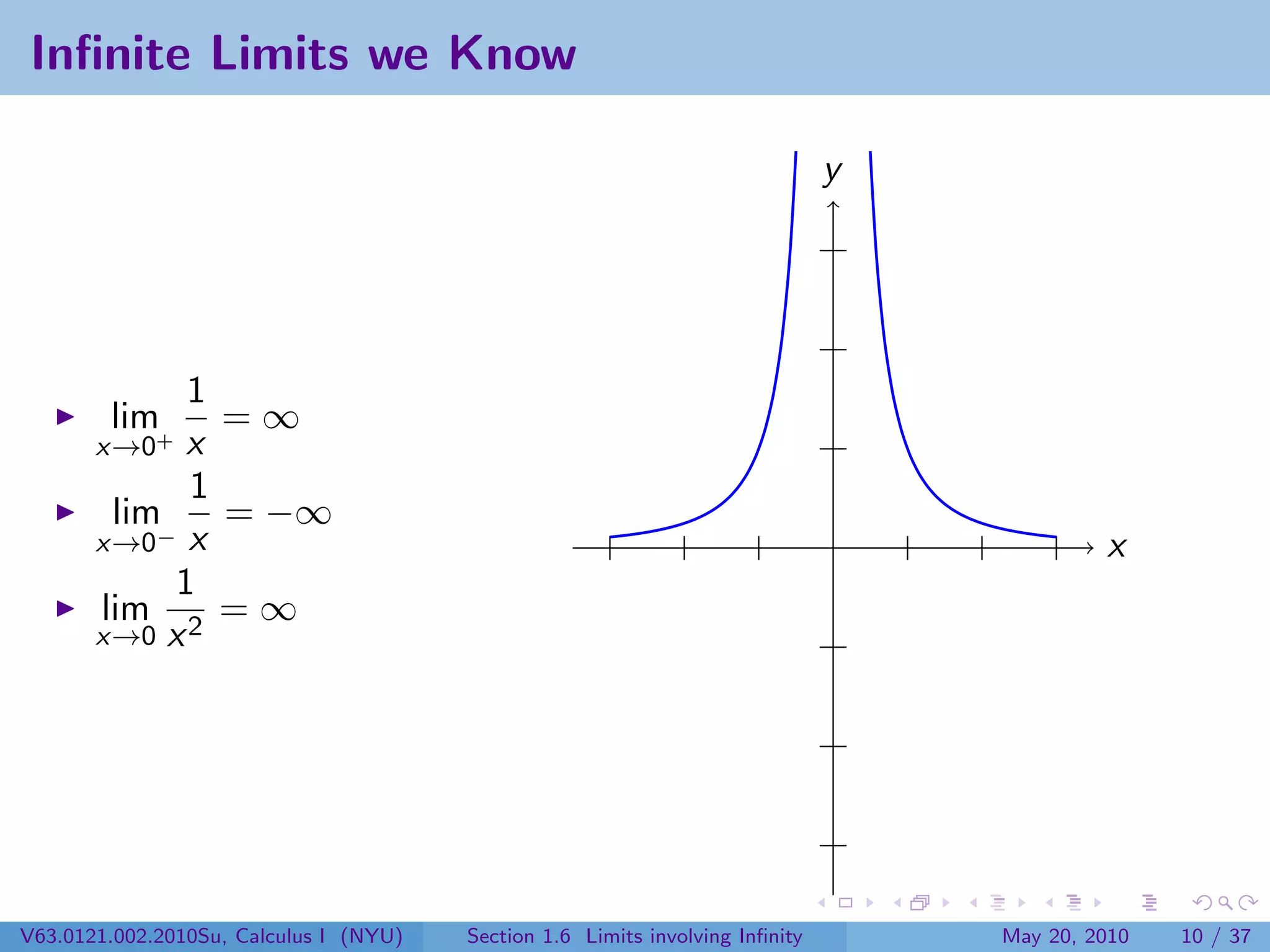
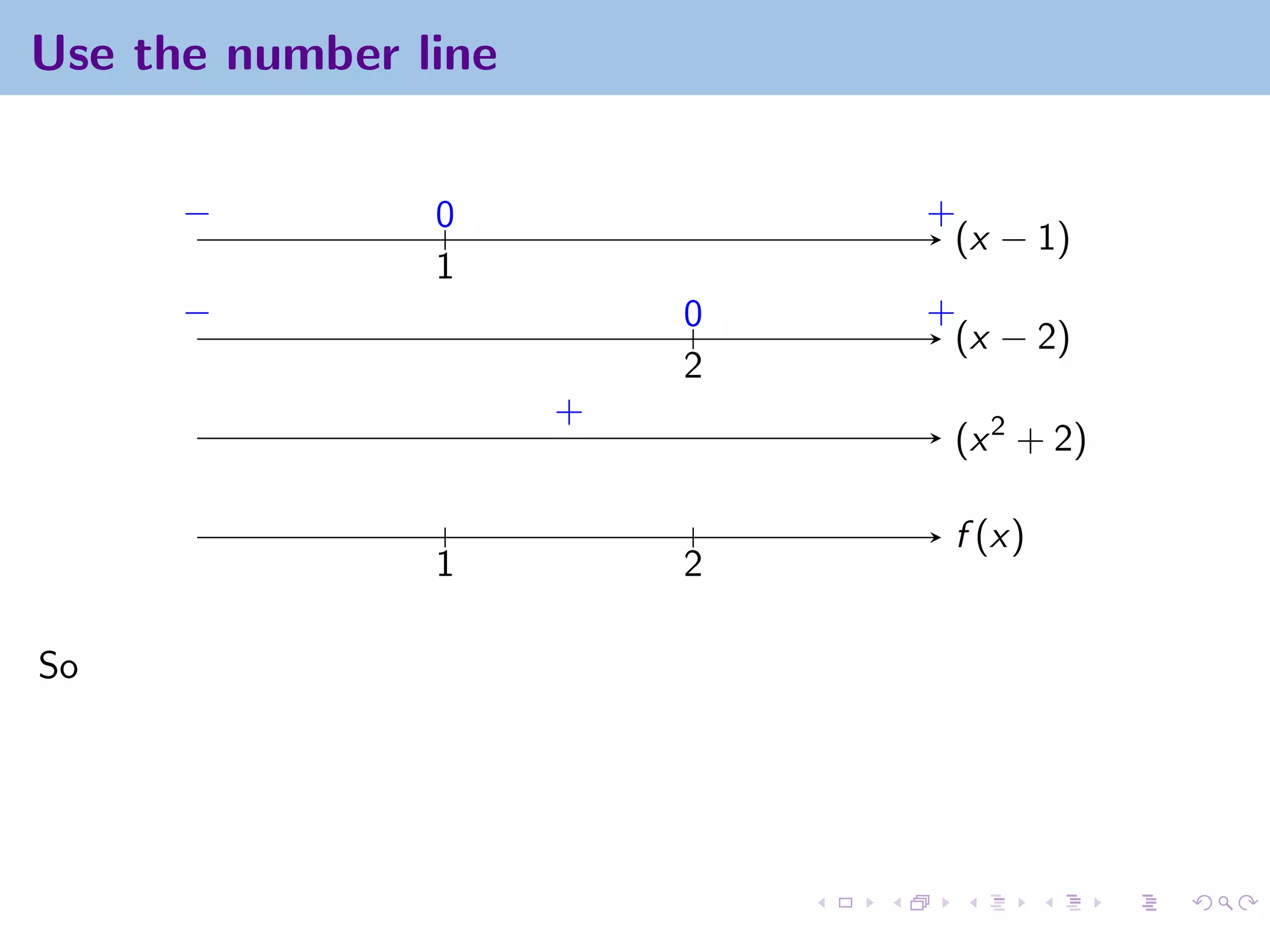
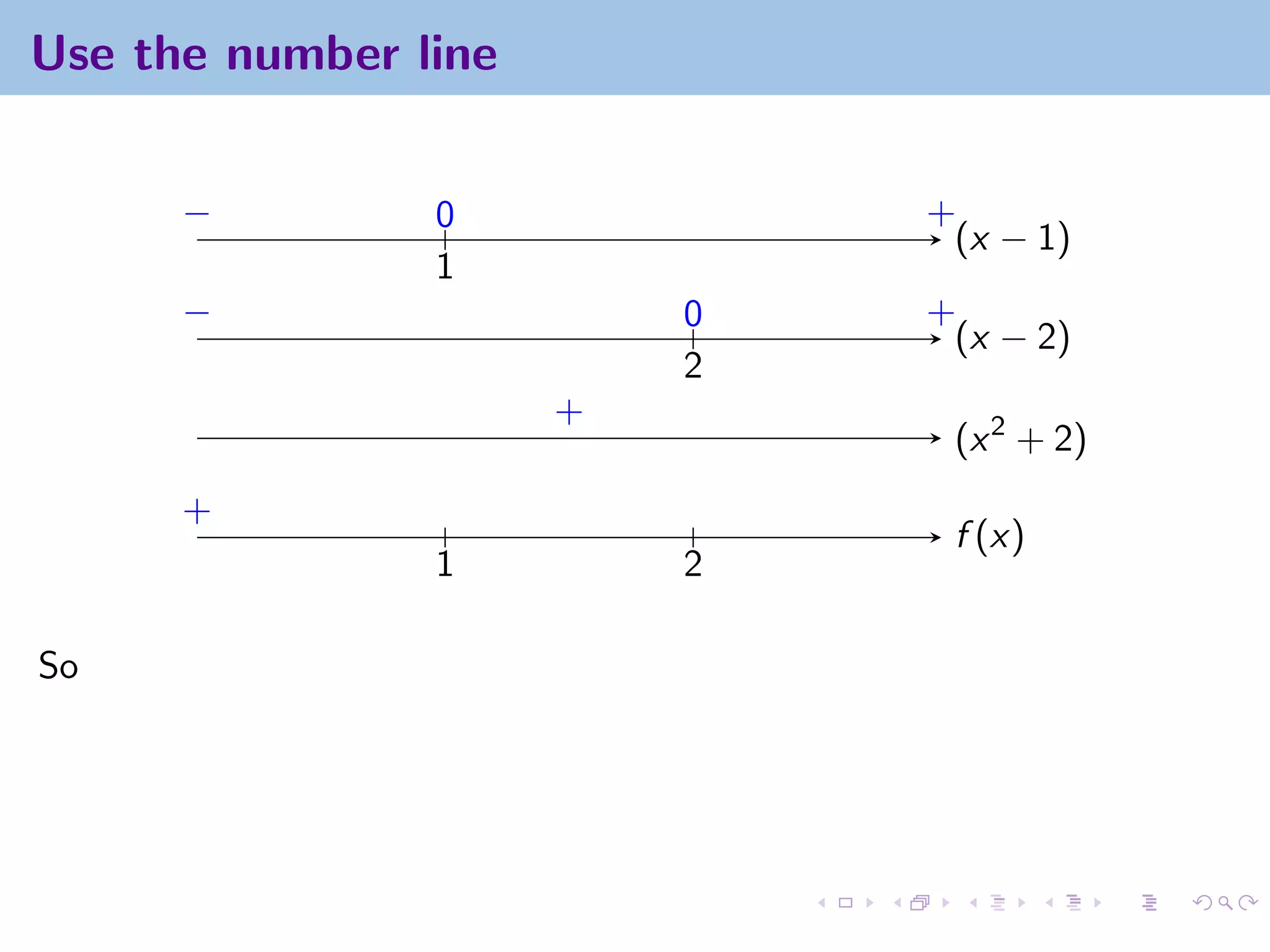
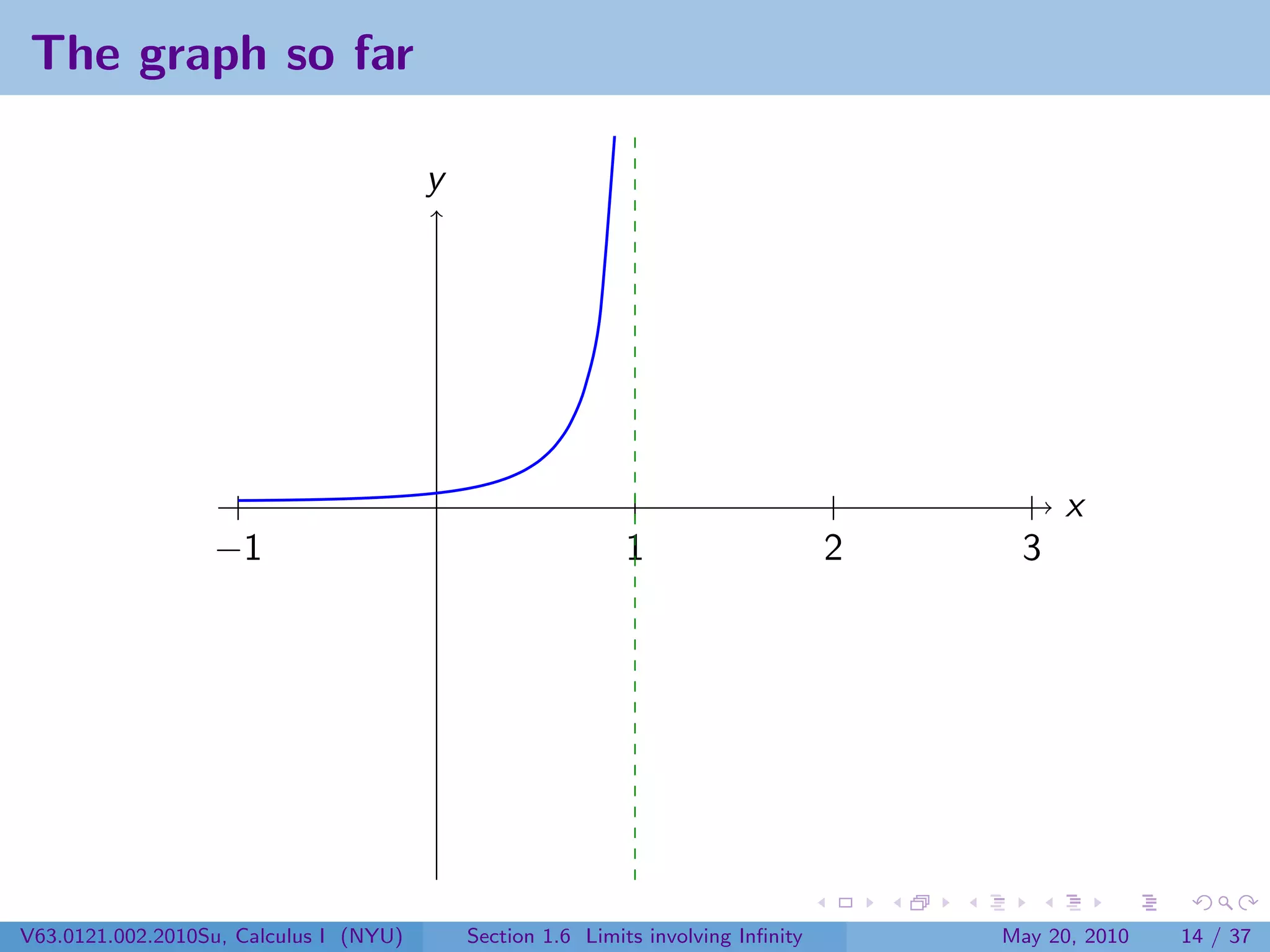
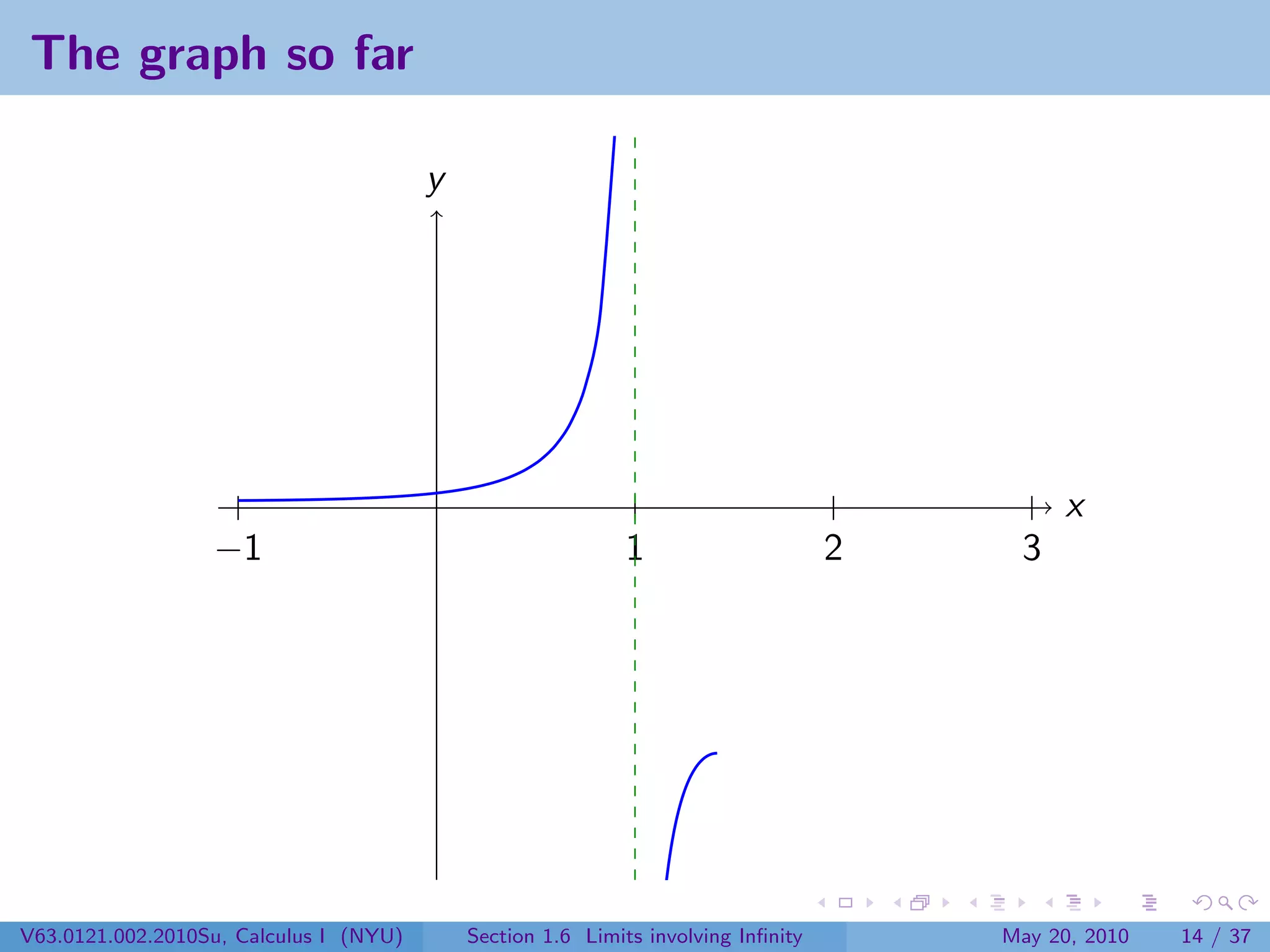
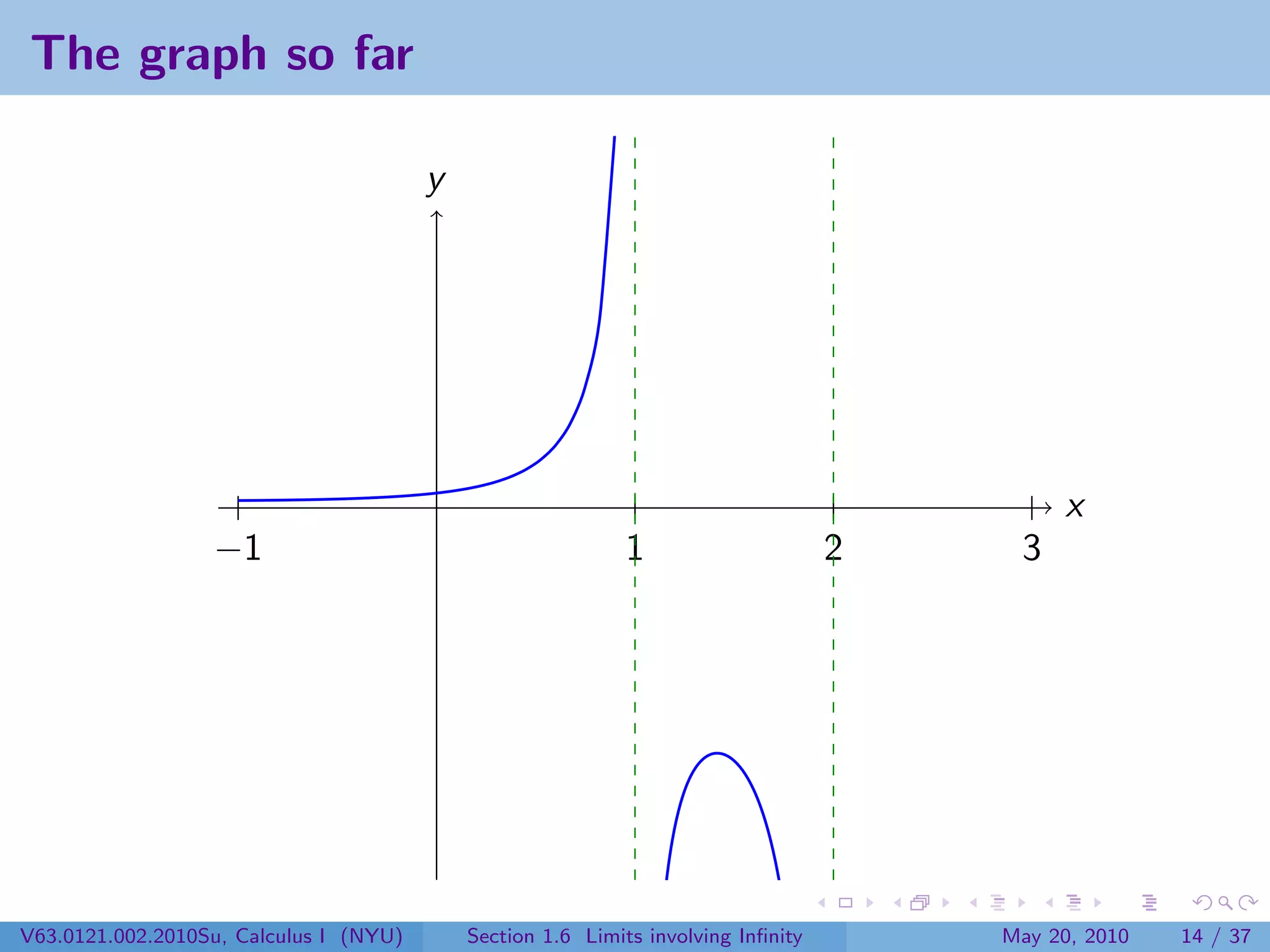
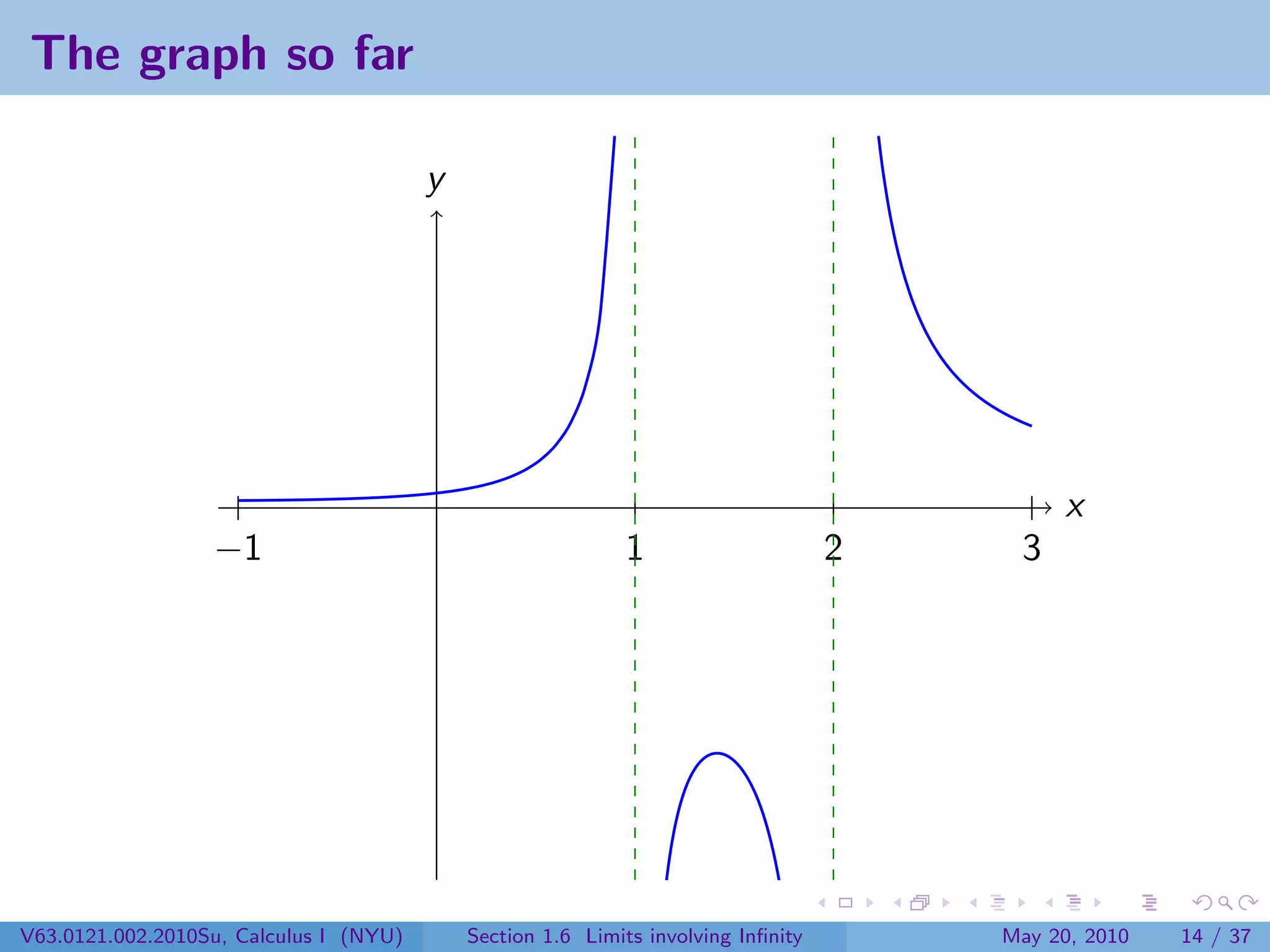
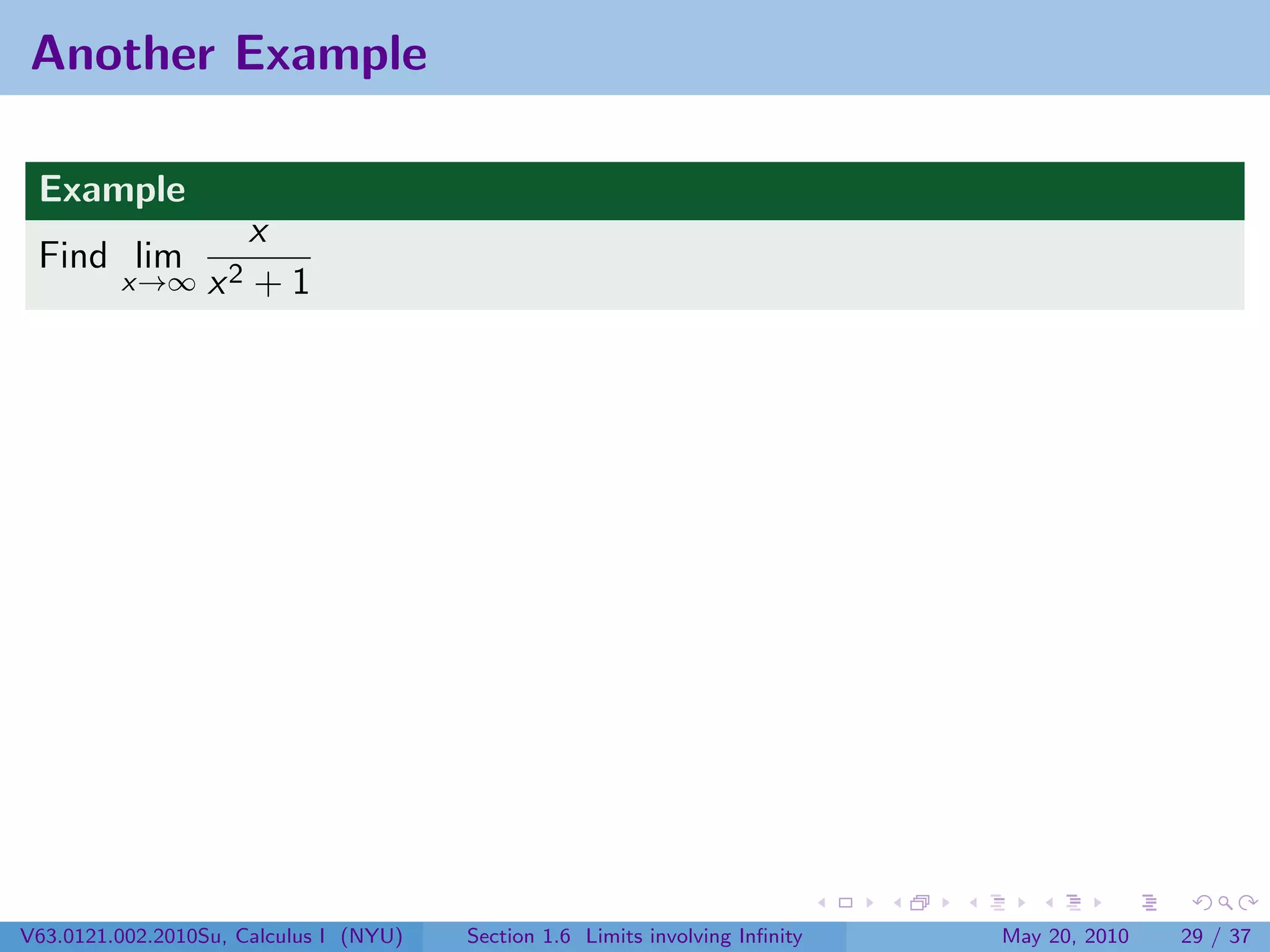
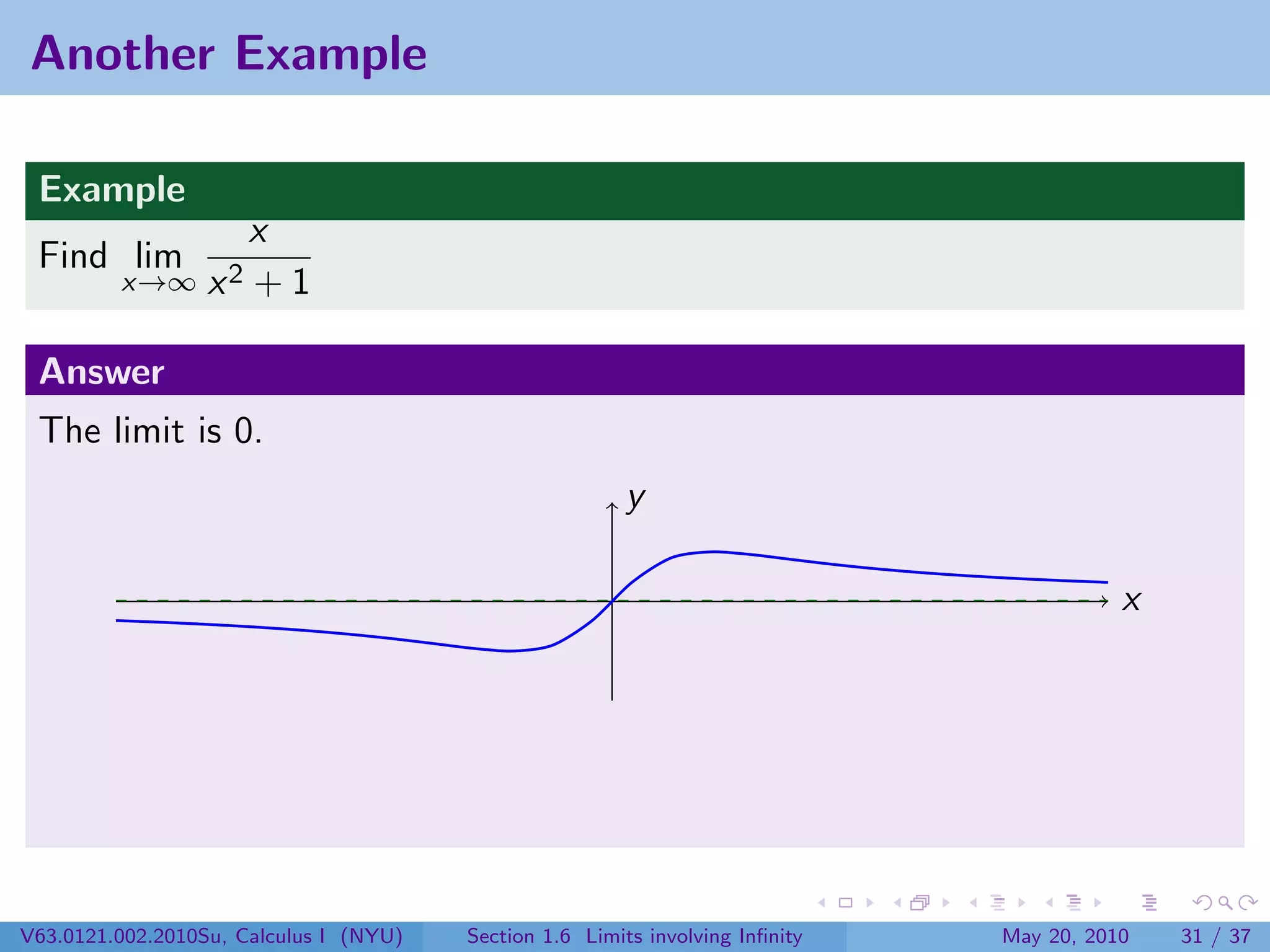
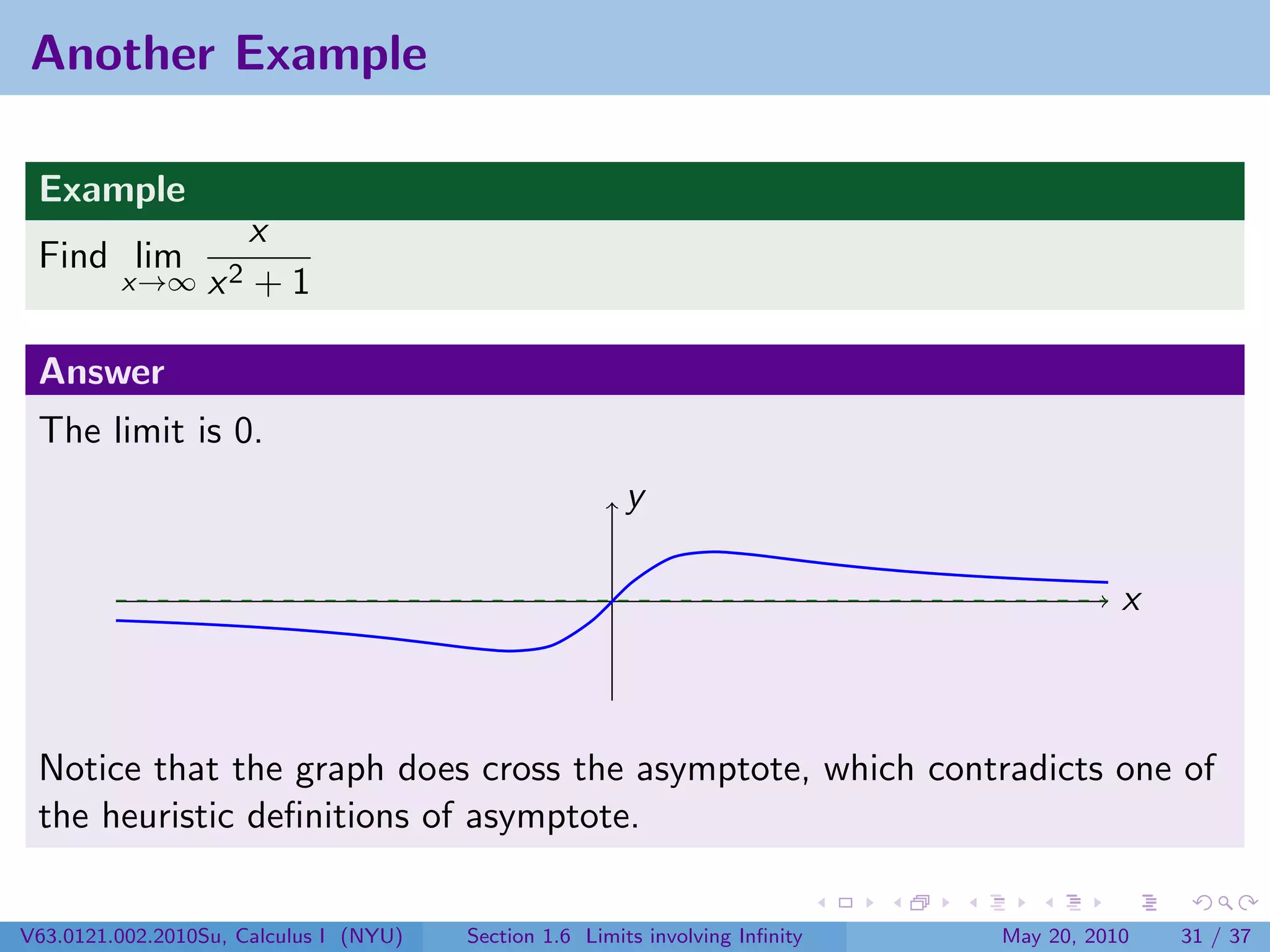
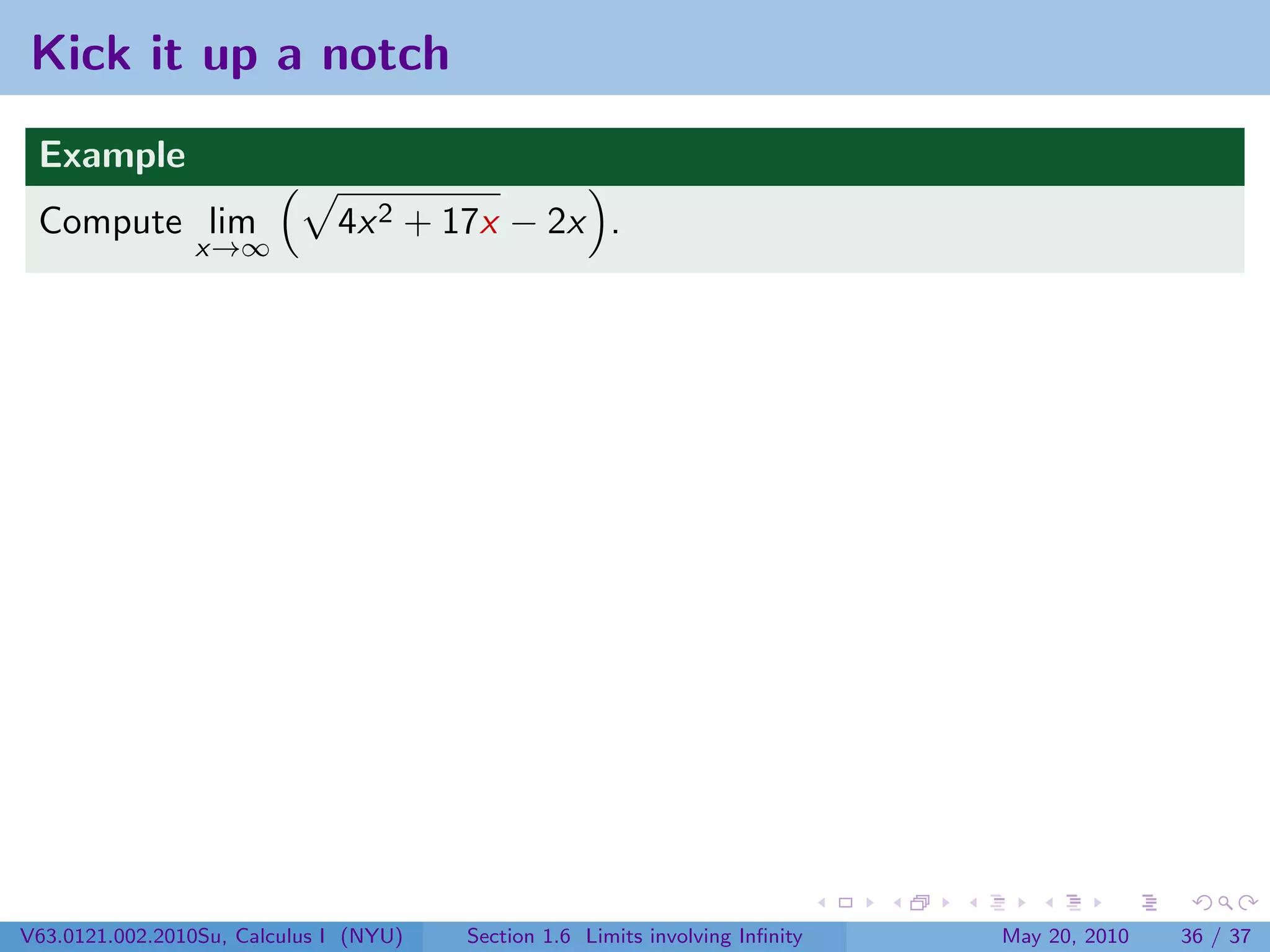
This document appears to be lecture notes on limits involving infinity from a Calculus I class at New York University. It begins with announcements about office hours and an upcoming quiz. It then reviews the definition of limits, discusses limits involving infinity like vertical asymptotes, and outlines topics to be covered like infinite limits, limit laws with infinity, and limits as x approaches infinity.