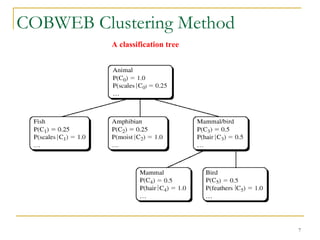
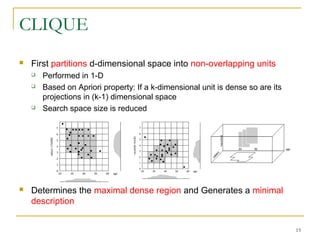
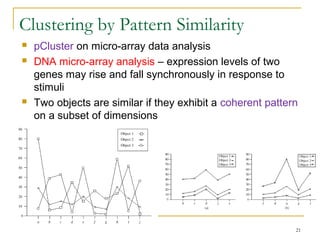
The document discusses various model-based clustering techniques for handling high-dimensional data, including expectation-maximization, conceptual clustering using COBWEB, self-organizing maps, subspace clustering with CLIQUE and PROCLUS, and frequent pattern-based clustering. It provides details on the methodology and assumptions of each technique.

1. Clustering
Model based techniques and Handling
high dimensional data
1

2. 2
Model-Based Clustering Methods
 Attempt to optimize the fit between the data and some mathematical
model
 Assumption: Data are generated by a mixture of underlying probability
distributions
 Techniques
 Expectation-Maximization
 Conceptual Clustering
 Neural Networks Approach

3. Expectation Maximization
 Each cluster is represented mathematically by a
parametric probability distribution
 Component distribution
 Data is a mixture of these distributions
 Mixture density model
 Problem: To estimate parameters of probability distributions
3

4. Expectation Maximization
 Iterative Refinement Algorithm – used to find parameter
estimates
 Extension of k-means
 Assigns an object to a cluster according to a weight representing
probability of membership
 Initial estimate of parameters
 Iteratively reassigns scores
4

5. Expectation Maximization
 Initial guess for parameters; randomly select k objects to
represent cluster means or centers
 Iteratively refine parameters / clusters
 Expectation Step
 Assign each object xi to cluster Ck with probability
where
 Maximization Step
 Re-estimate model parameters
 Simple and easy to implement
 Complexity depends on features, objects and iterations
5

6. 6
Conceptual Clustering
 Conceptual clustering
 A form of clustering in machine learning
 Produces a classification scheme for a set of unlabeled objects
 Finds characteristic description for each concept (class)
 COBWEB
 A popular and simple method of incremental conceptual learning
 Creates a hierarchical clustering in the form of a classification tree
 Each node refers to a concept and contains a probabilistic description
of that concept

7. 7
COBWEB Clustering Method
A classification tree

8. COBWEB
 Classification tree
 Each node – Concept and its probabilistic distribution
(Summary of objects under that node)
 Description – Conditional probabilities P(Ai=vij / Ck)
 Sibling nodes at given level form a partition
 Category Utility
 Increase in the expected number of attribute values that can
be correctly guessed given a partition
8

9. COBWEB
 Category Utility rewards:
 Intra-class similarity P(Ai=vij|Ck)
 High value indicates many class members share this attribute-value
pair
 Inter-class dissimilarity P(Ck|Ai=vij)
 High values – fewer objects in different classes share this attribute-
value
 Placement of new objects
 Descend tree
 Identify best host
 Temporarily place object in each node and compute CU of resulting
partition
 Placement with highest CU is chosen
 COBWEB may also forms new nodes if object does not fit into the
existing tree
9

10. COBWEB
 COBWEB is sensitive to order of records
 Additional operations
 Merging and Splitting
 Two best hosts are considered for merging
 Best host is considered for splitting
 Limitations
 The assumption that the attributes are independent of each
other is often too strong because correlation may exist
 Not suitable for clustering large database data
 CLASSIT - an extension of COBWEB for incremental clustering of
continuous data
10

11. Neural Network Approach
 Represent each cluster as an exemplar, acting as a “prototype” of
the cluster
 New objects are distributed to the cluster whose exemplar is the
most similar according to some distance measure
 Self Organizing Map
 Competitive learning
 Involves a hierarchical architecture of several units (neurons)
 Neurons compete in a “winner-takes-all” fashion for the object currently
being presented
 Organization of units – forms a feature map
 Web Document Clustering
11

12. Kohenen SOM
12

13. Clustering High-Dimensional data
 As dimensionality increases
 number of irrelevant dimensions may produce noise and mask real clusters
 data becomes sparse
 Distance measures –meaningless
 Feature transformation methods
 PCA, SVD – Summarize data by creating linear combinations of attributes
 But do not remove any attributes; transformed attributes – complex to
interpret
 Feature Selection methods
 Most relevant set of attributes with respect to class labels
 Entropy Analysis
 Subspace Clustering – searches for groups of clusters within different
subspaces of the same data set
13

14. CLIQUE: CLustering In QUest
 Dimension growth subspace clustering
 Starts at 1-D and grows upwards to higher dimensions
 Partitions each dimension – grids – determines whether
cell is dense
 CLIQUE
 Determines sparse and crowded units
 Dense unit – fraction of data points > threshold
 Cluster – maximal set of connected dense units
14

15. CLIQUE
 First partitions d-dimensional space into non-overlapping units
 Performed in 1-D
 Based on Apriori property: If a k-dimensional unit is dense so are its
projections in (k-1) dimensional space
 Search space size is reduced
 Determines the maximal dense region and Generates a minimal
description
15

16. CLIQUE
 Finds subspace of highest dimension
 Insensitive to order of inputs
 Performance depends on grid size and density threshold
 Difficult to determine across all dimensions
 Several lower dimensional subspaces will have to be
processed
 Can use adaptive strategy
16

17. PROCLUS – PROjected CLUStering
 Dimension-reduction Subspace Clustering technique
 Finds initial approximation of clusters in high dimensional
space
 Avoids generation of large number of overlapped
clusters of lower dimensionality
 Finds best set of medoids by hill-climbing process
(Similar to CLARANS)
 Manhattan Segmental distance measure
17

18. PROCLUS
 Initialization phase
 Greedy algorithm to select a set of initial medoids that are far
apart
 Iteration Phase
 Selects a random set of k-medoids
 Replaces bad medoids
 For each medoid a set of dimensions is chosen whose average
distances are small
 Refinement Phase
 Computes new dimensions for each medoid based on clusters
found, reasigns points to medoids and removes outliers
18

19. Frequent Pattern based Clustering
 Frequent patterns may also form clusters
 Instead of growing clusters dimension by dimension sets
of frequent itemsets are determined
 Two common technqiues
 Frequent term-based text Clustering
 Clustering by Pattern similarity
19

20. Frequent-term based text clustering
 Text documents are clustered based on frequent terms
they contain
 Documents – terms
 Dimensionality is very high
 Frequent term based analysis
 Well selected subset of set of all frequent terms must be
discovered
 Fi – Set of frequent term sets
 Cov(Fi) – set of documents covered by Fi
 ∑i=1 k
cov(Fi) = D and overlap between Fi and Fj must be
minimized
 Description of clusters – their frequent term sets
20

21. Clustering by Pattern Similarity
 pCluster on micro-array data analysis
 DNA micro-array analysis – expression levels of two
genes may rise and fall synchronously in response to
stimuli
 Two objects are similar if they exhibit a coherent pattern
on a subset of dimensions
21

22. pCluster
 Shift Pattern discovery
 Euclidean distance – not suitable
 Derive new attributes
 Bi-Clustering based on mean squared residue score
 pCluster
 Objects –x, y; attributes – a, b
 A pair (O,T) forms a δ-pCluster if for any 2 x 2 matrix X in (O, T)
pScore(X) <= δ
 Each pair of objects and their features must satisfy threshold
22

23. pCluster
 Scaling patterns
 pCluster can be used in other applications
also
23