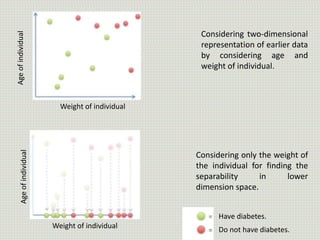
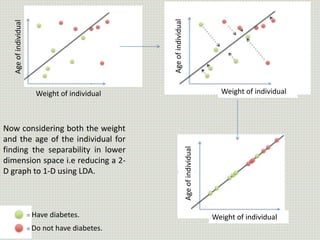
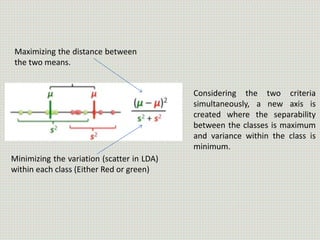
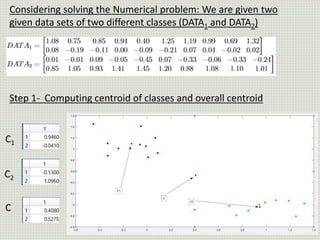
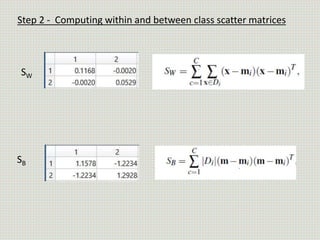
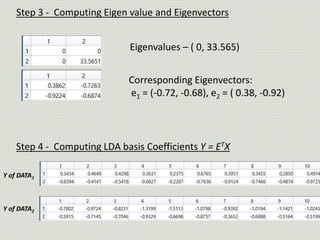
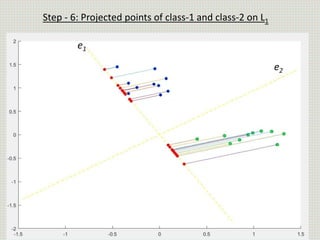
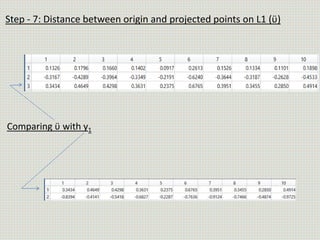
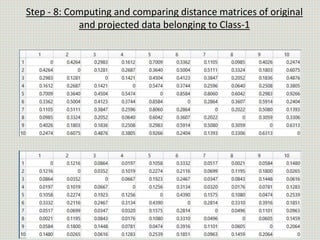
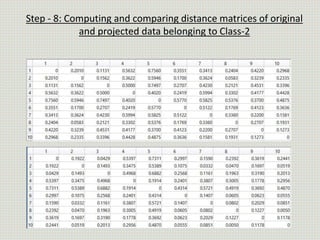
The document discusses the application of linear discriminant analysis (LDA) to determine an individual's propensity for diabetes based on their weight and age. It outlines the methodology for maximizing class separability and minimizing variance through scatter matrices and eigenvalue computation. The process includes several steps, including calculating centroids, projecting data onto a hyperplane, and comparing distances of original and projected data points for two different classes.

1. Linear Discriminant Analysis (LDA)
Batch Number – 04
107115009
107115075
108115034
108115058
108115062
108115103

2. Problem Statement;
• Aim: To decide whether a person is prone to diabetes or
not.
- Deciding based on the person’s weight.
Have diabetes.
Do not have diabetes.
Weight of individual

3. Weight of individual
AgeofindividualAgeofindividual
Weight of individual
Have diabetes.
Do not have diabetes.
Considering two-dimensional
representation of earlier data
by considering age and
weight of individual.
Considering only the weight of
the individual for finding the
separability in lower
dimension space.

4. Weight of individual
Ageofindividual
Have diabetes.
Do not have diabetes.
Now considering both the weight
and the age of the individual for
finding the separability in lower
dimension space i.e reducing a 2-
D graph to 1-D using LDA.
Weight of individual
Weight of individual
Ageofindividual
Ageofindividual

5. Maximizing the distance between
the two means.
Minimizing the variation (scatter in LDA)
within each class (Either Red or green)
Considering the two criteria
simultaneously, a new axis is
created where the separability
between the classes is maximum
and variance within the class is
minimum.

6. Compute centroids of
Individual and overall
classes
Compute within class( SB ) &
between class (SW ) scatter
matrix
Maximize the objective
function and get SW
-1 SB
Obtain Eigen values &
vectors
Coefficients of LDA basis
Y = ETX
Project the points onto
hyper plane
Flowchart of LDA Algorithm

7. Considering solving the Numerical problem: We are given two
given data sets of two different classes (DATA1 and DATA2)
Step 1- Computing centroid of classes and overall centroid
C1
C2
C

8. SW
SB
Step 2 - Computing within and between class scatter matrices

9. Step 3 - Computing Eigen value and Eigenvectors
Eigenvalues – ( 0, 33.565)
Corresponding Eigenvectors:
e1 = (-0.72, -0.68), e2 = ( 0.38, -0.92)
Step 4 - Computing LDA basis Coefficients Y = ETX
Y of DATA1
Y of DATA2

10. Step 5 - Computing and Comparing X, X1, X2
x1 = y1 e1 + y2 e2
x2 = y1 e1
Corresponding
Eigenvectors:
e1 , e2
X of DATA1
X1
X2

11. e1
e2
Step - 6: Projected points of class-1 and class-2 on L1

12. Step - 7: Distance between origin and projected points on L1 (ϋ)
Comparing ϋ with y1

13. Step - 8: Computing and comparing distance matrices of original
and projected data belonging to Class-1

14. Step - 8: Computing and comparing distance matrices of original
and projected data belonging to Class-2

15. Contributions:
• 107115009 -
• 108115058 -