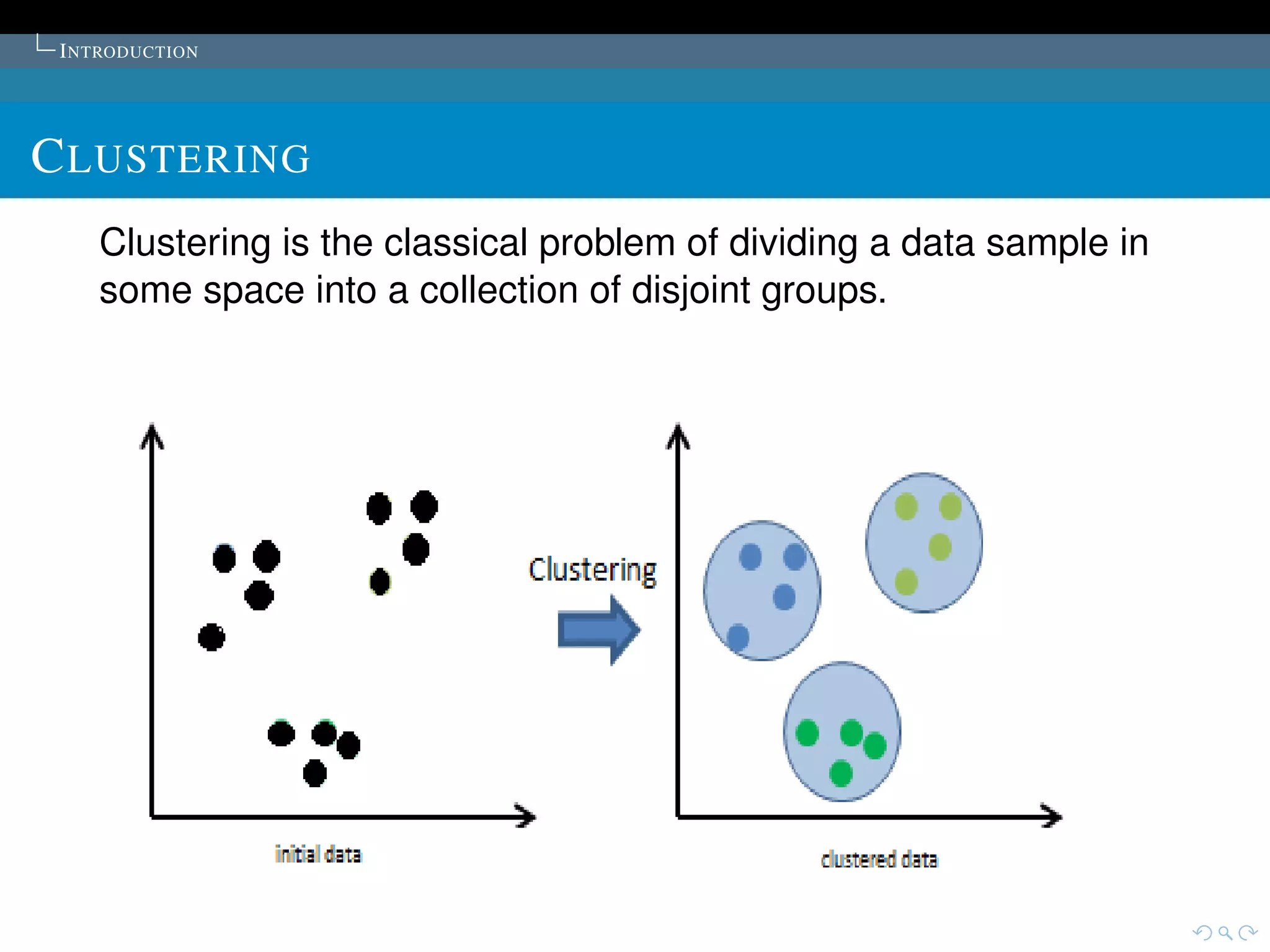
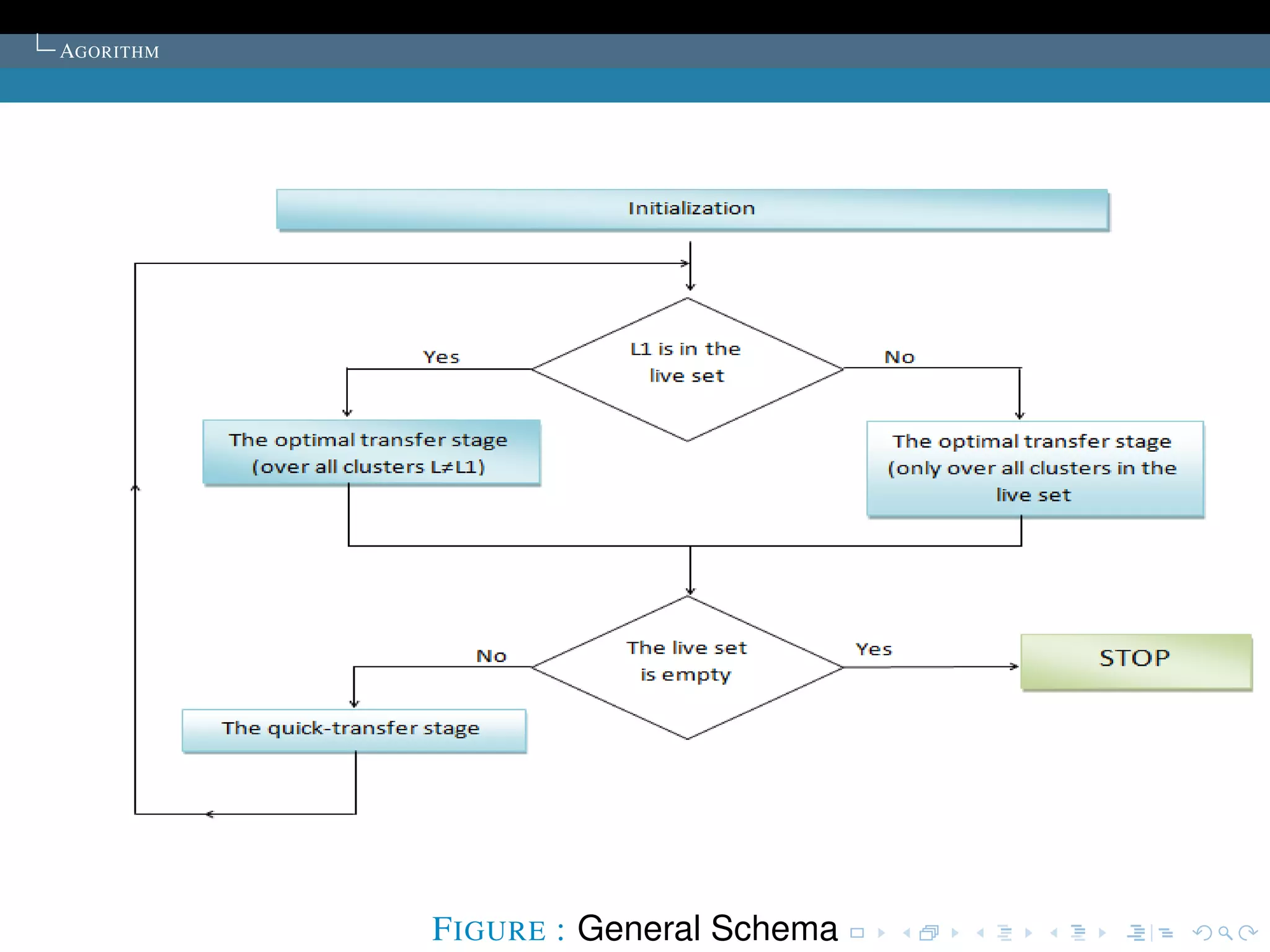
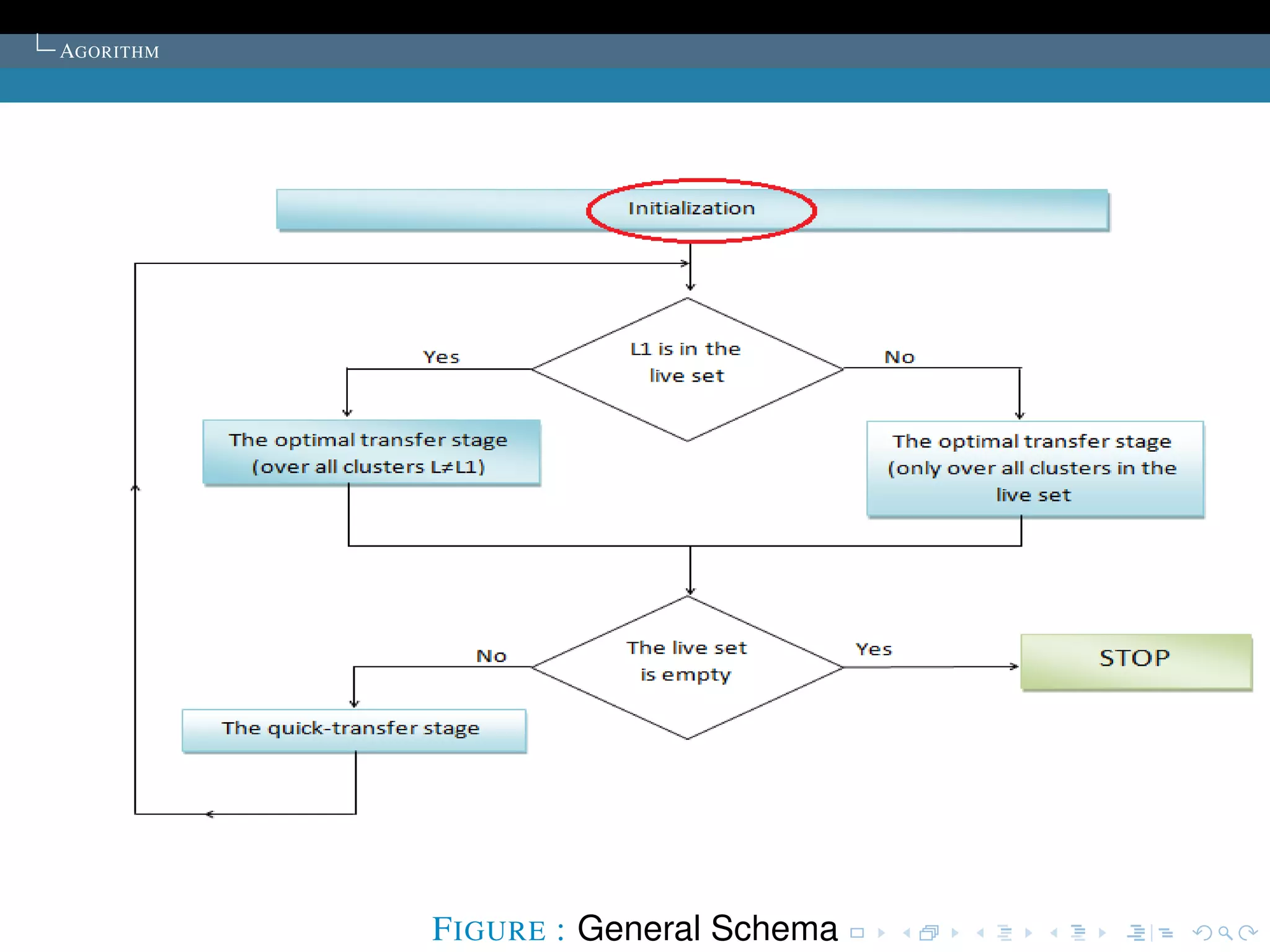
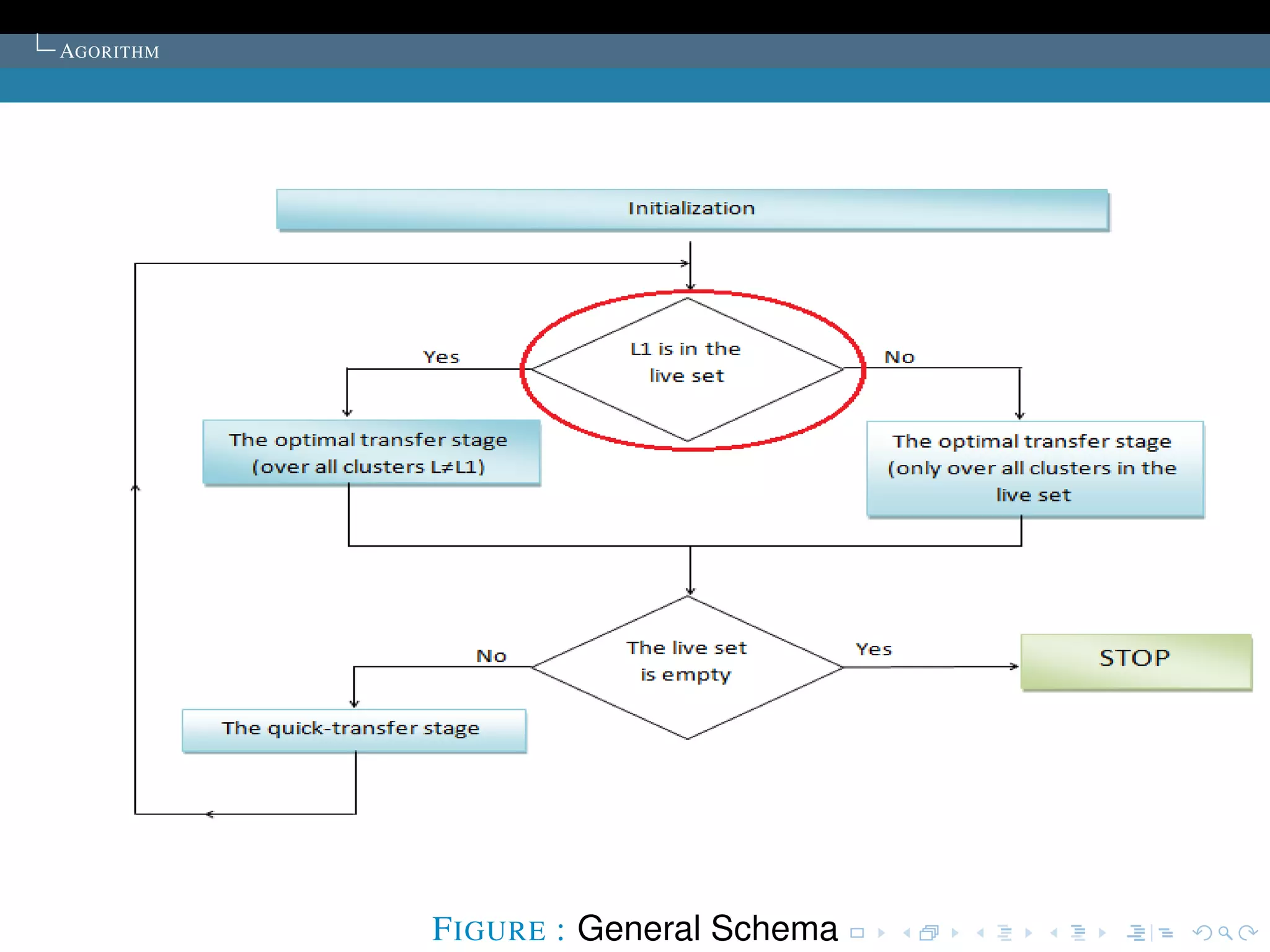
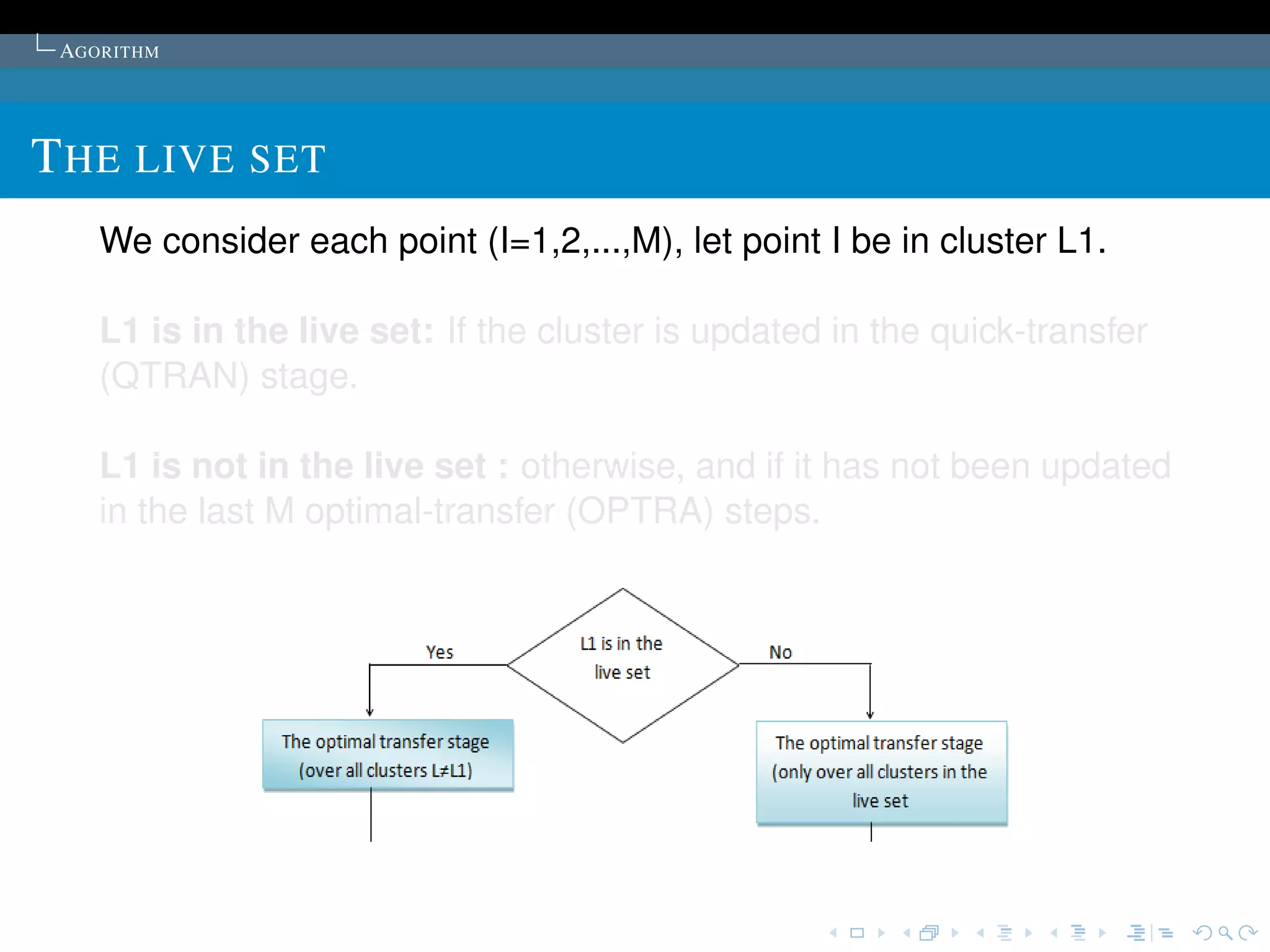
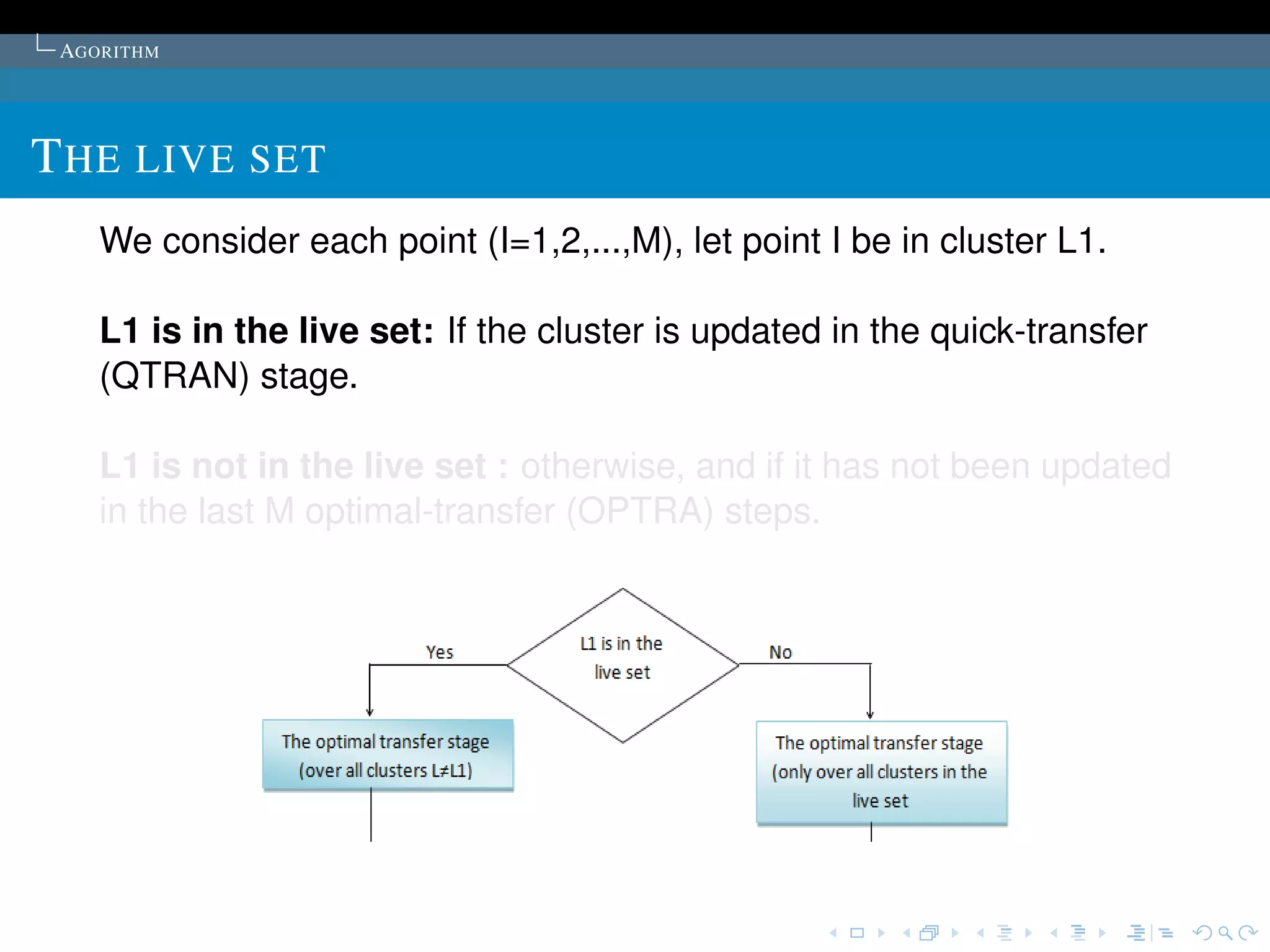
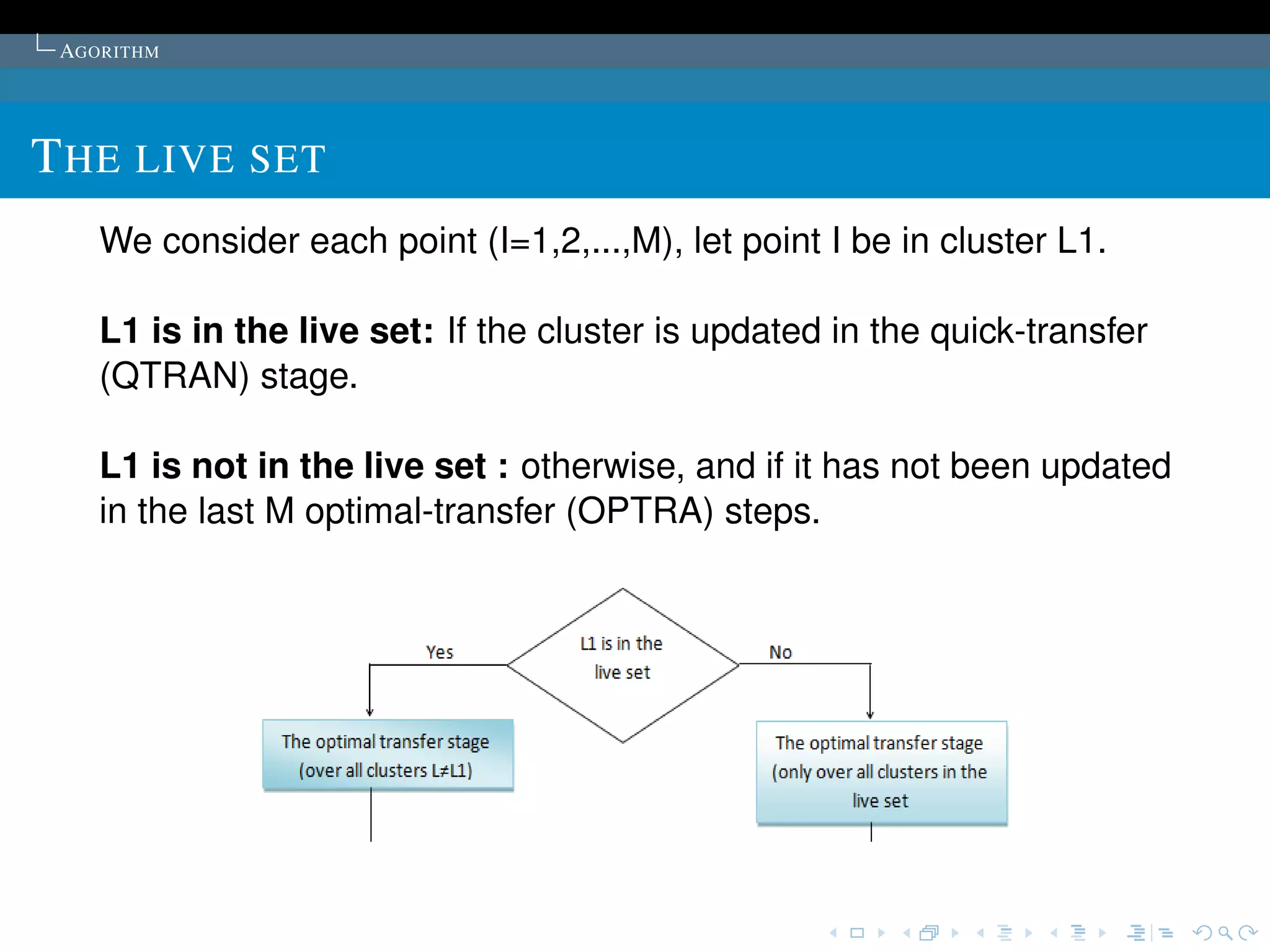
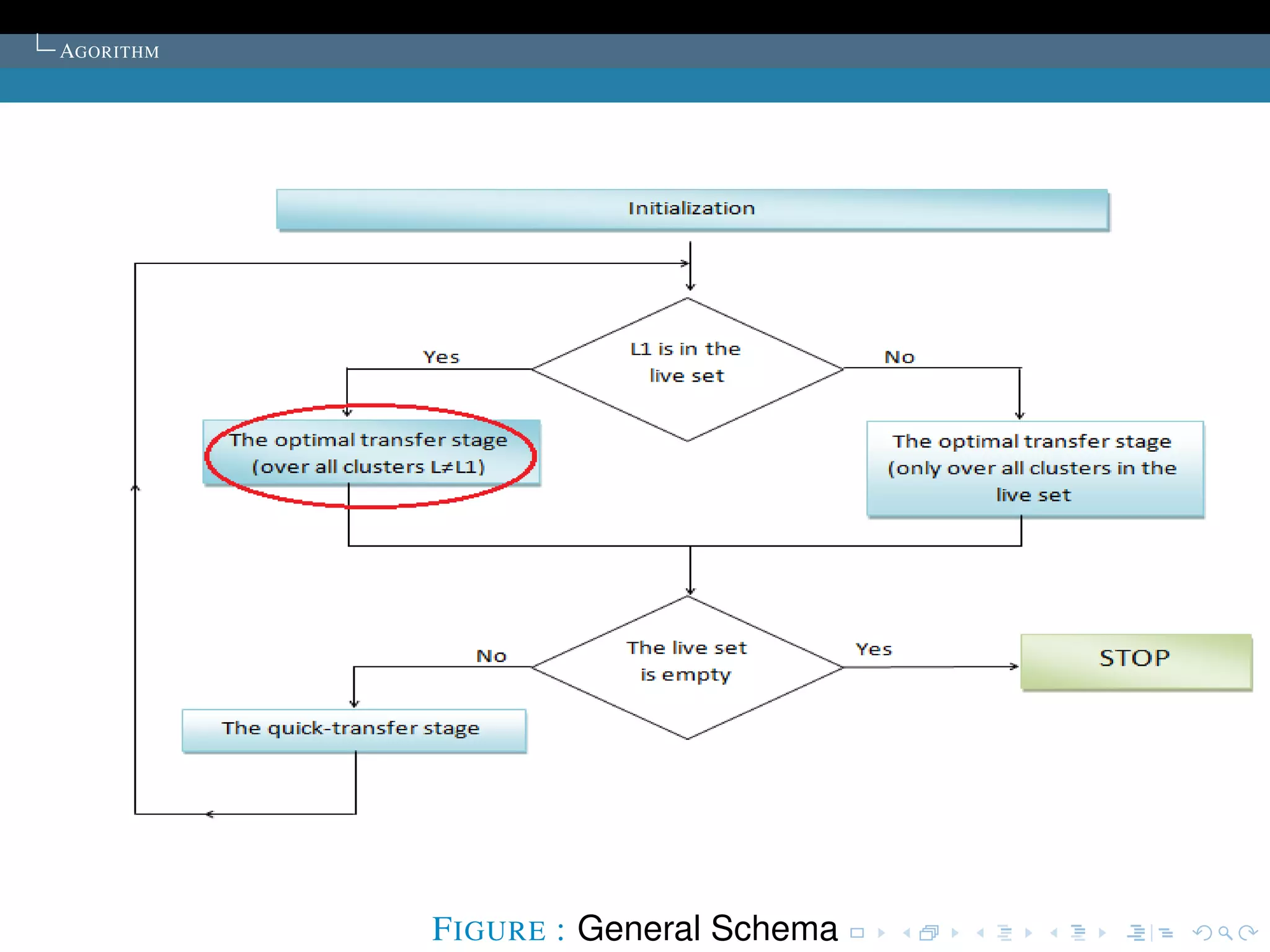
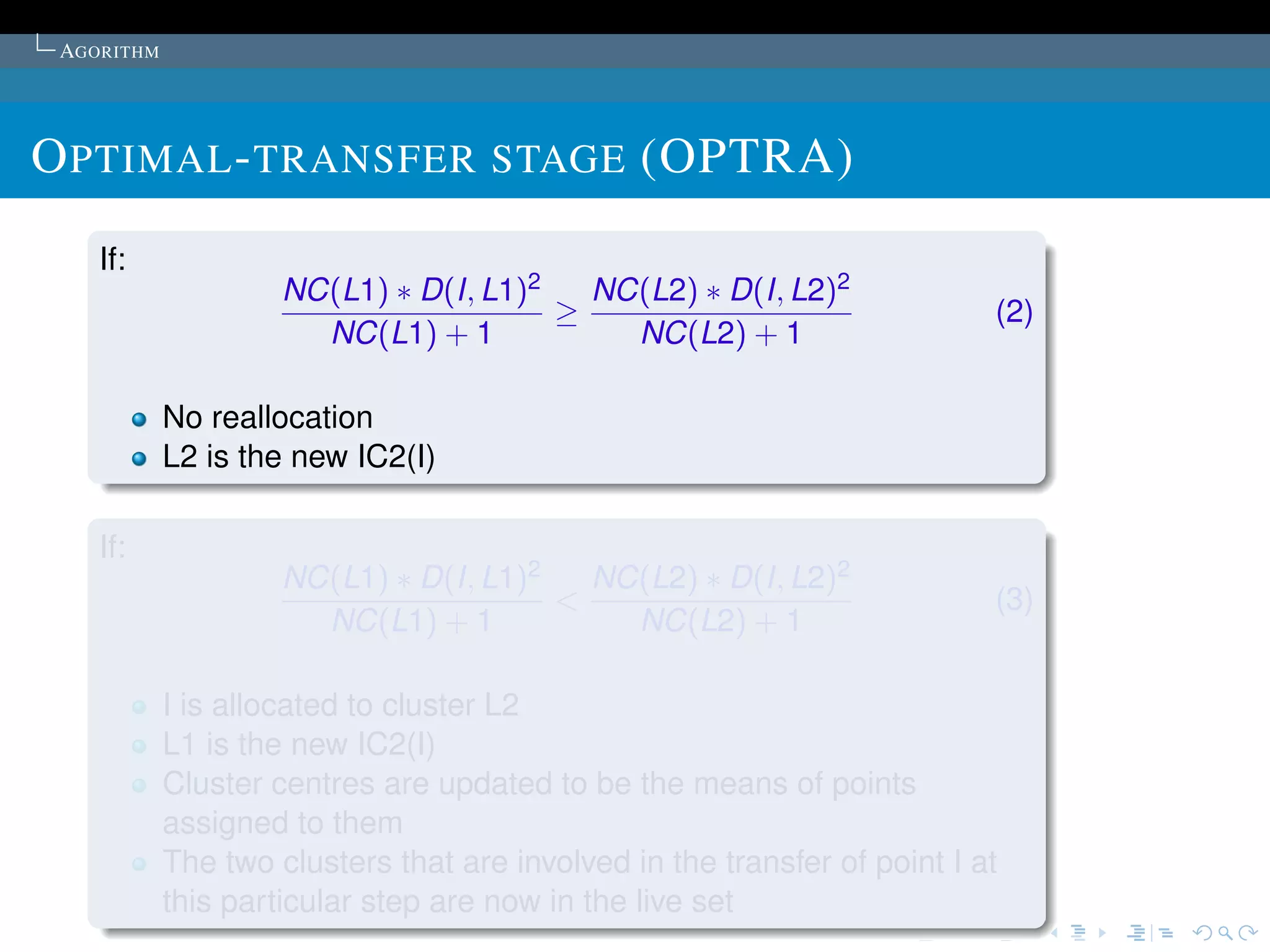
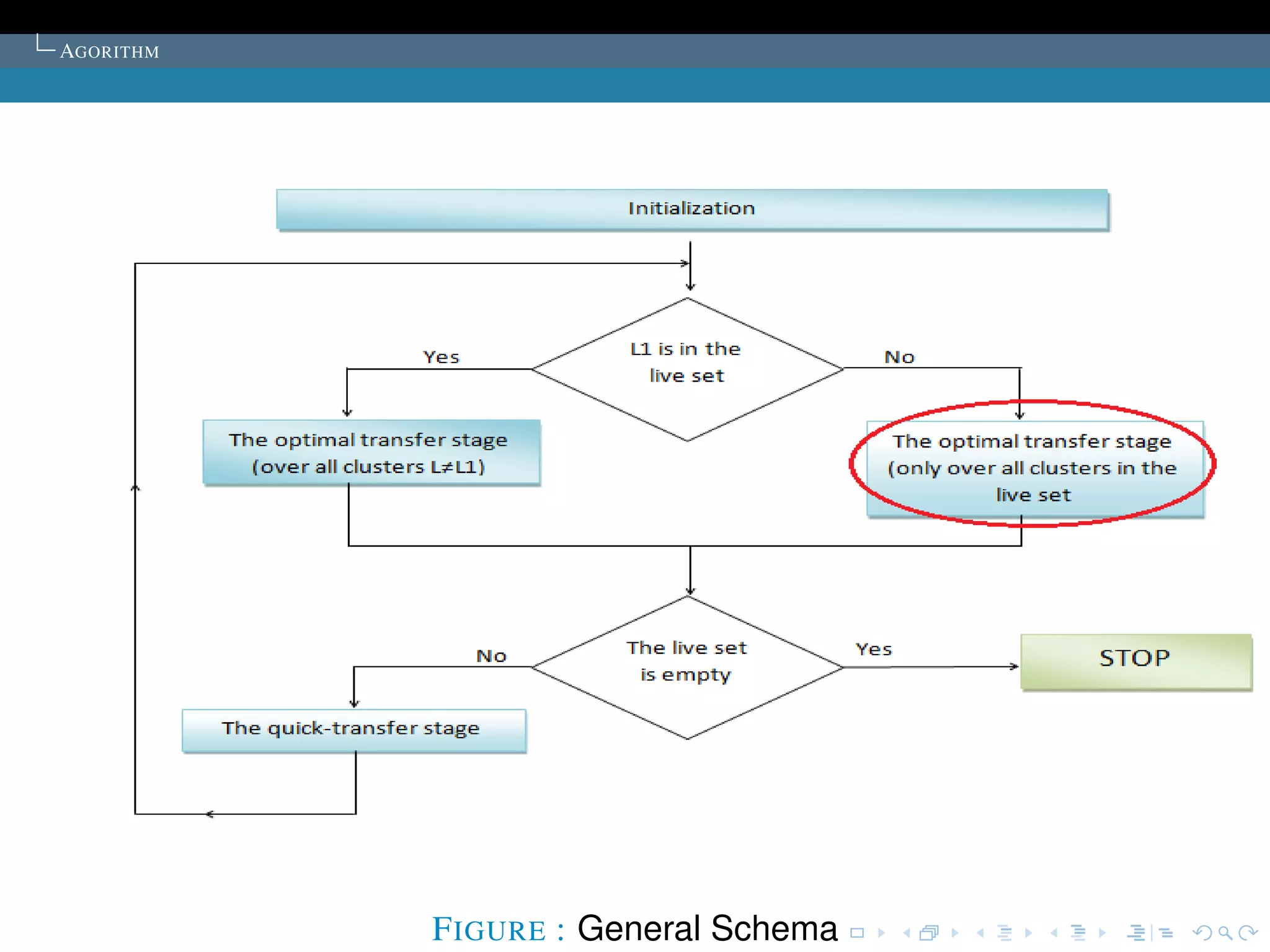
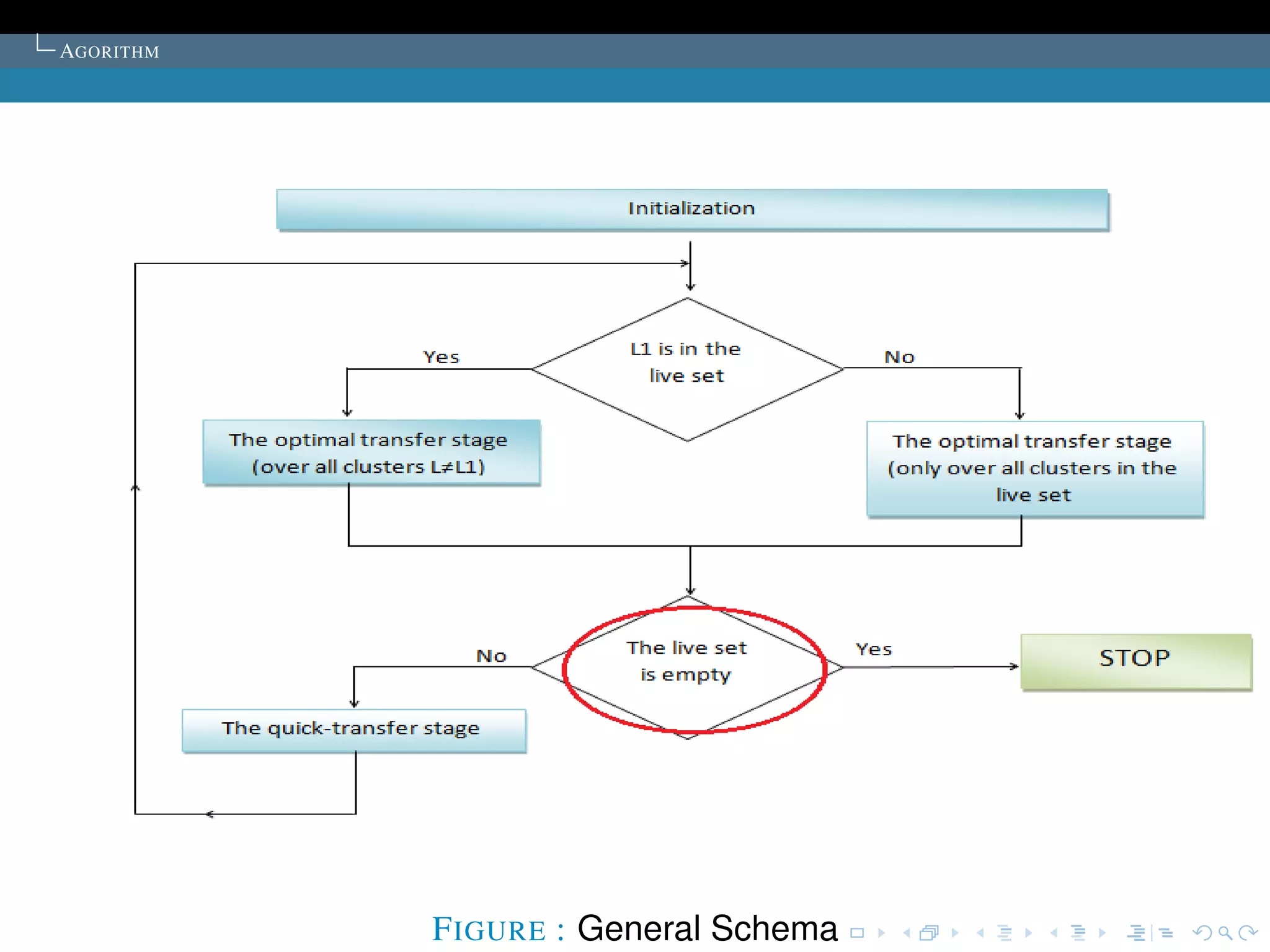
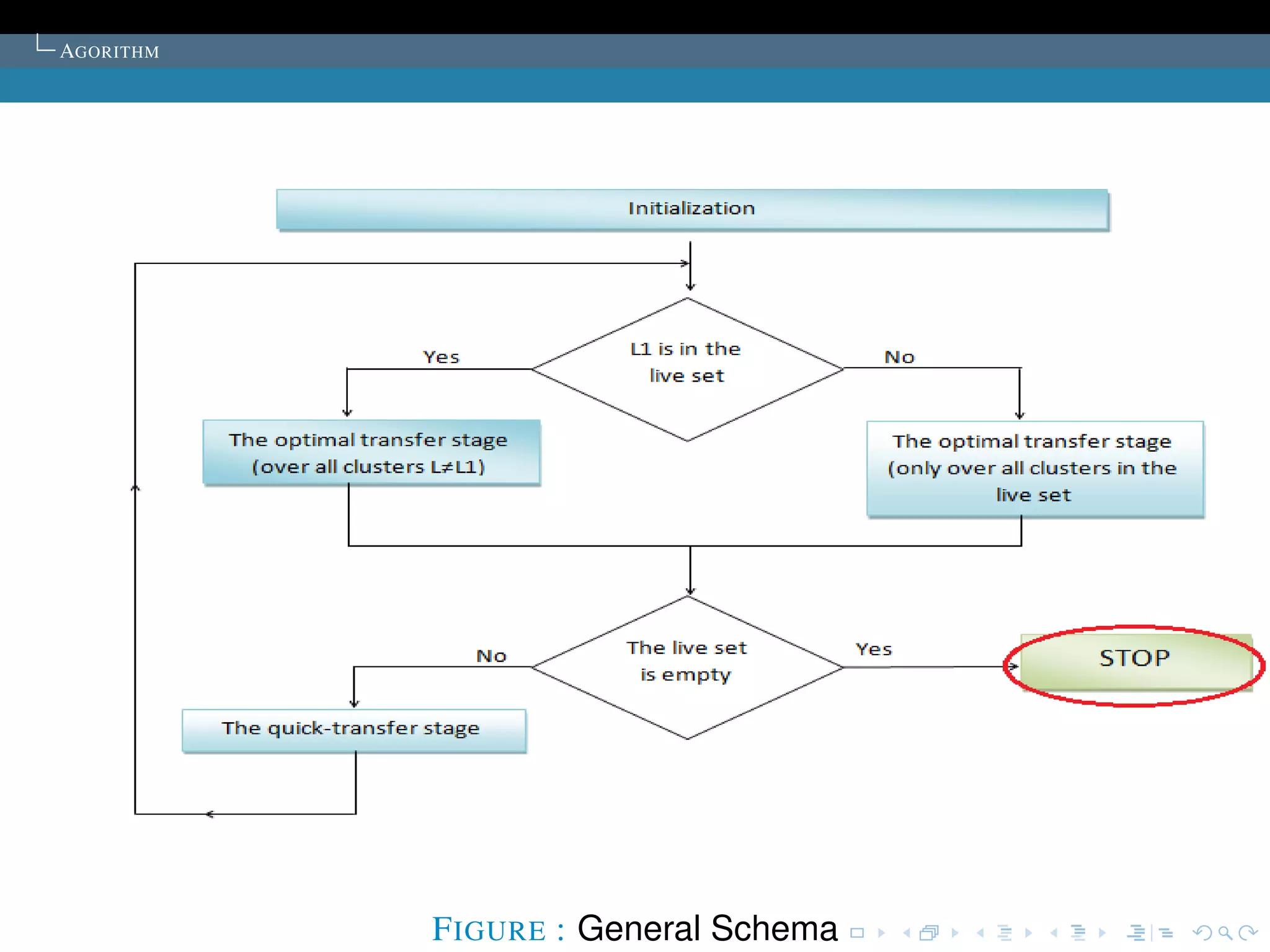
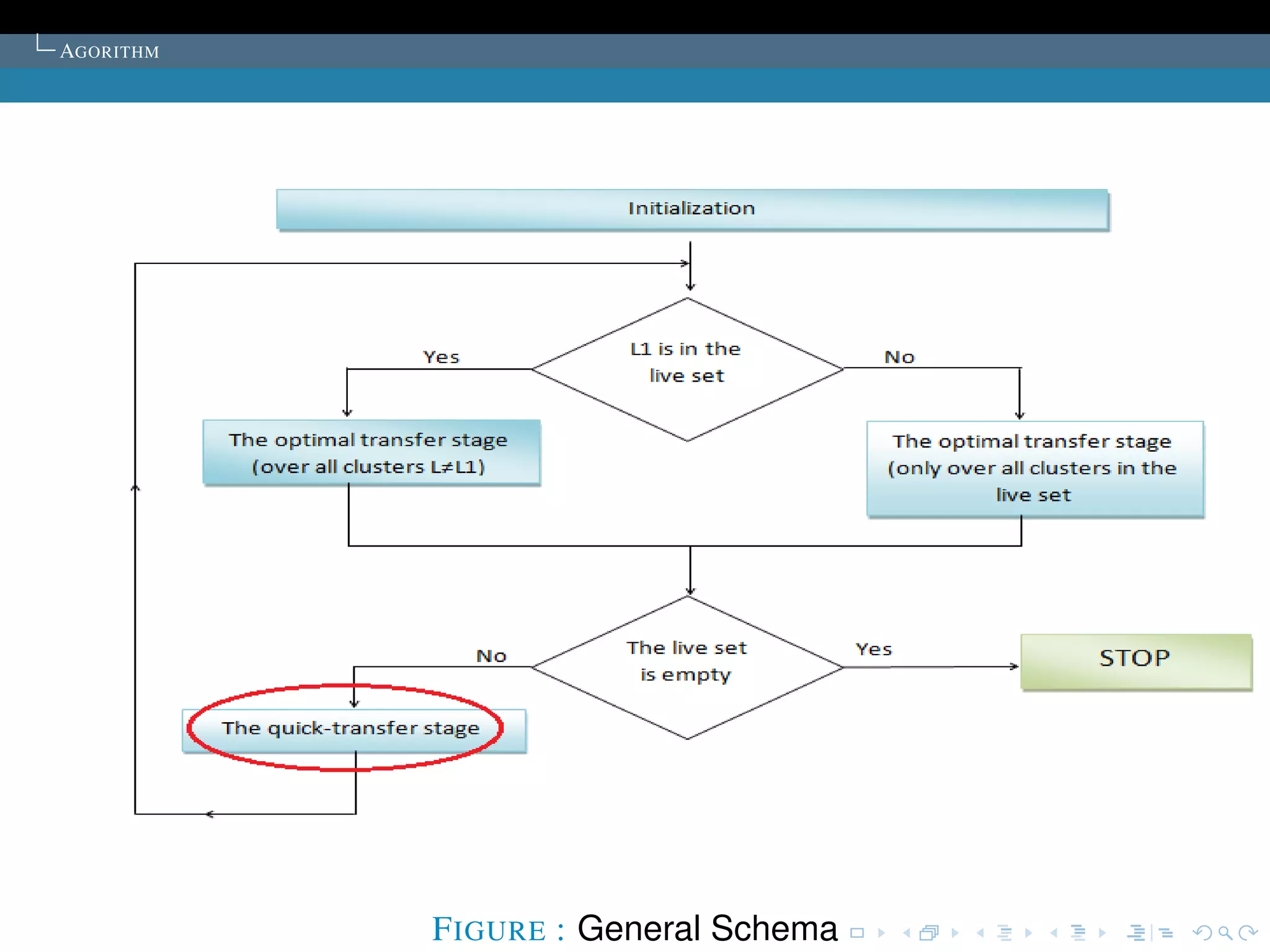
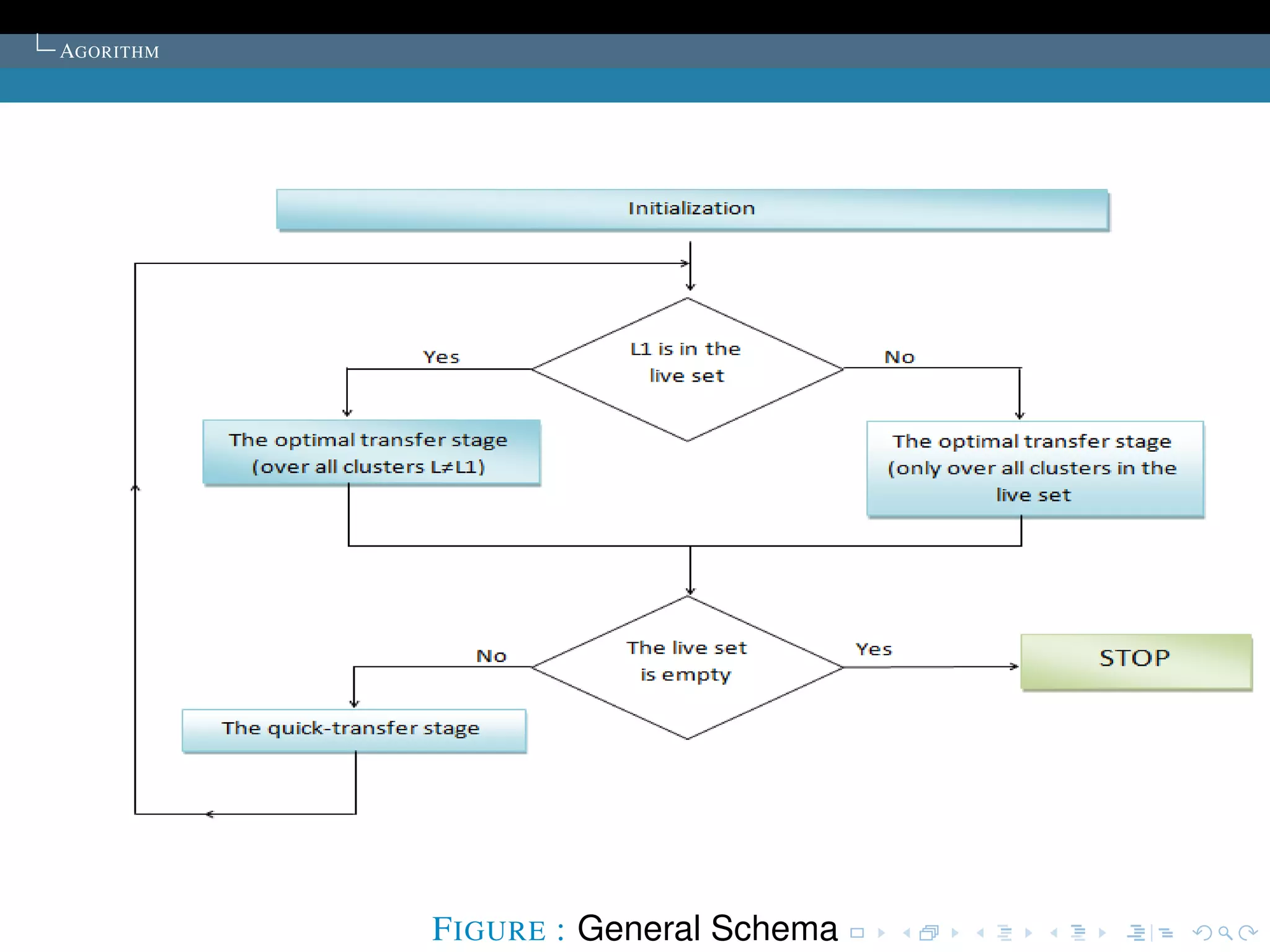
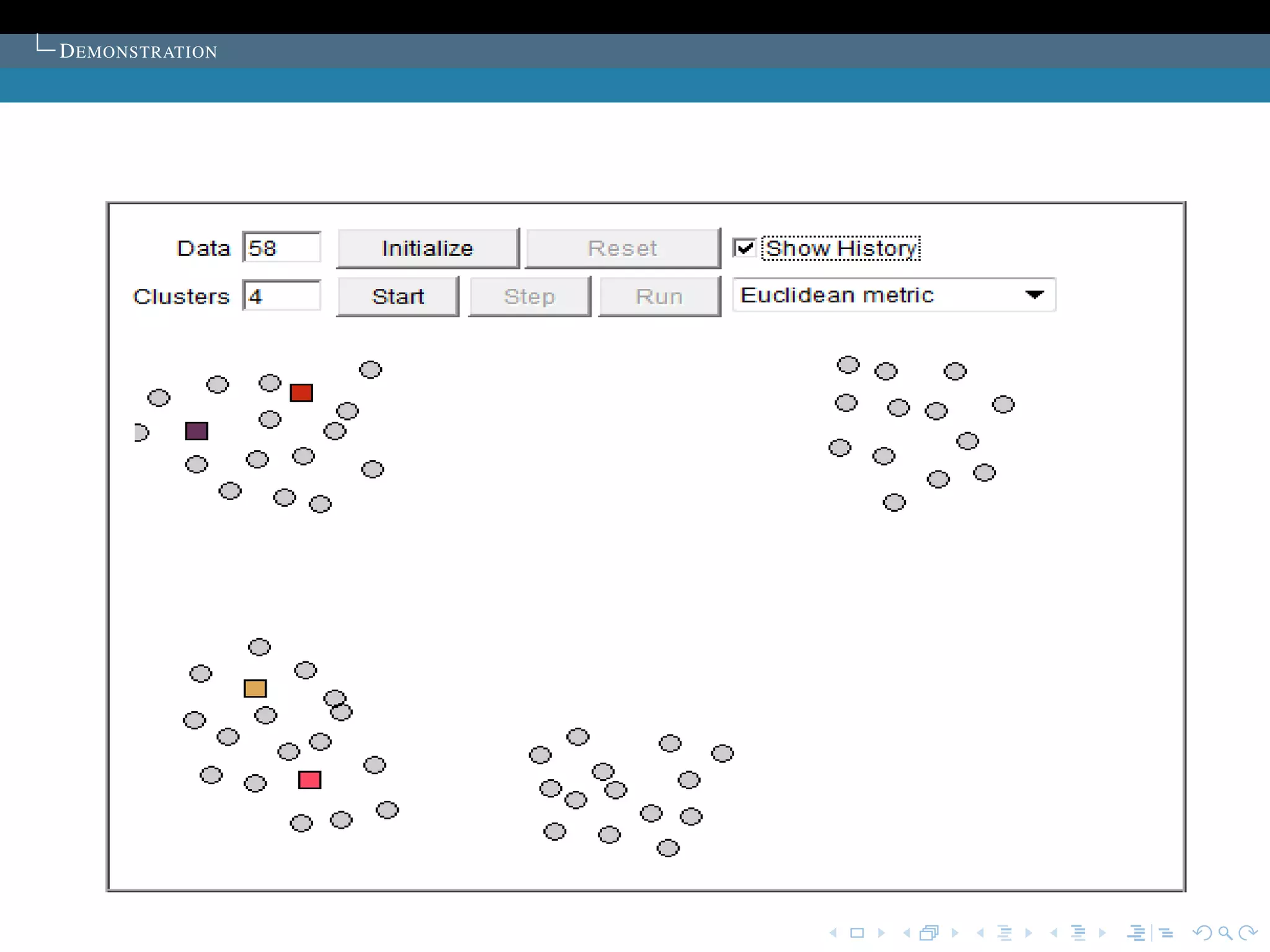
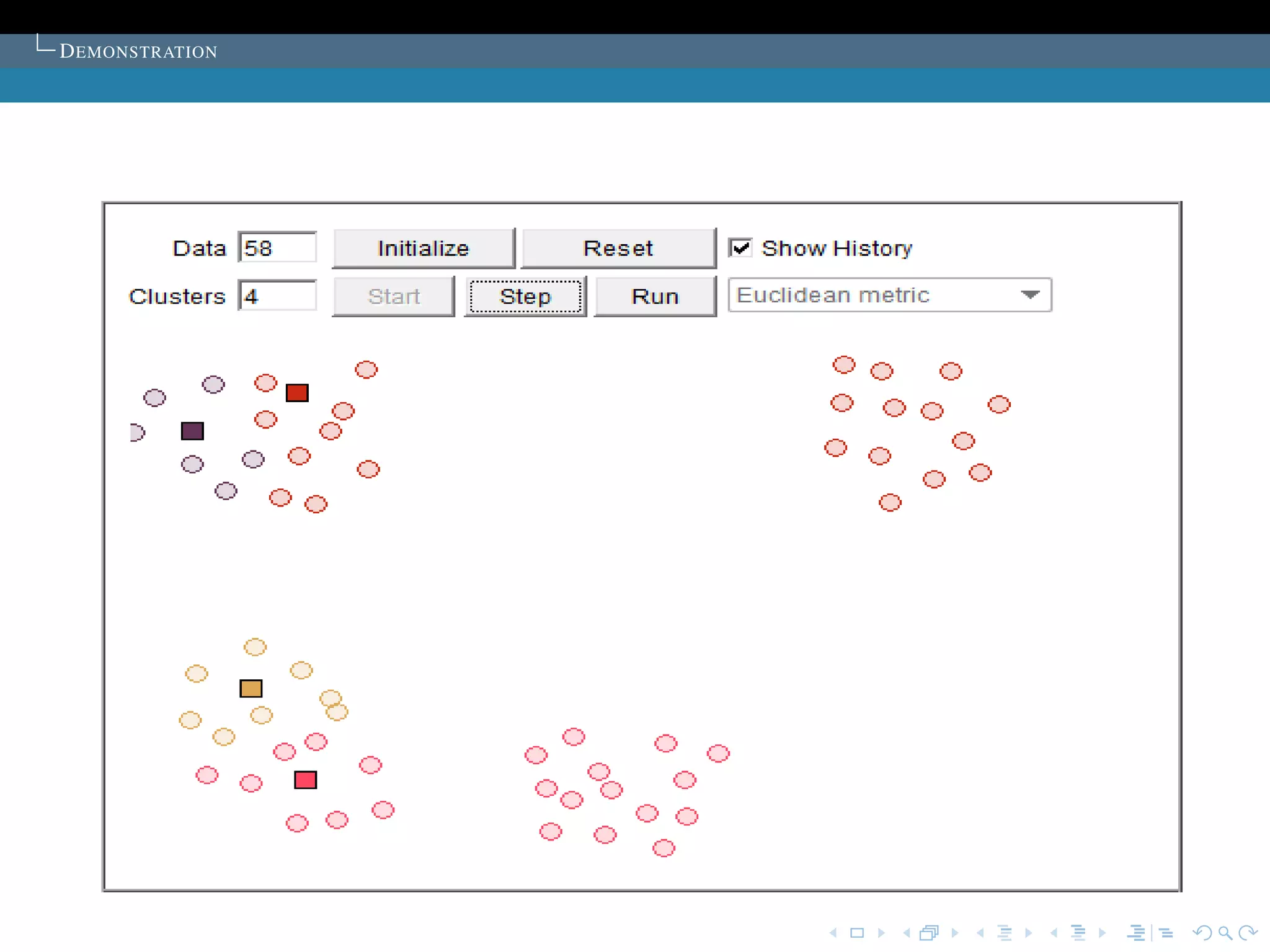
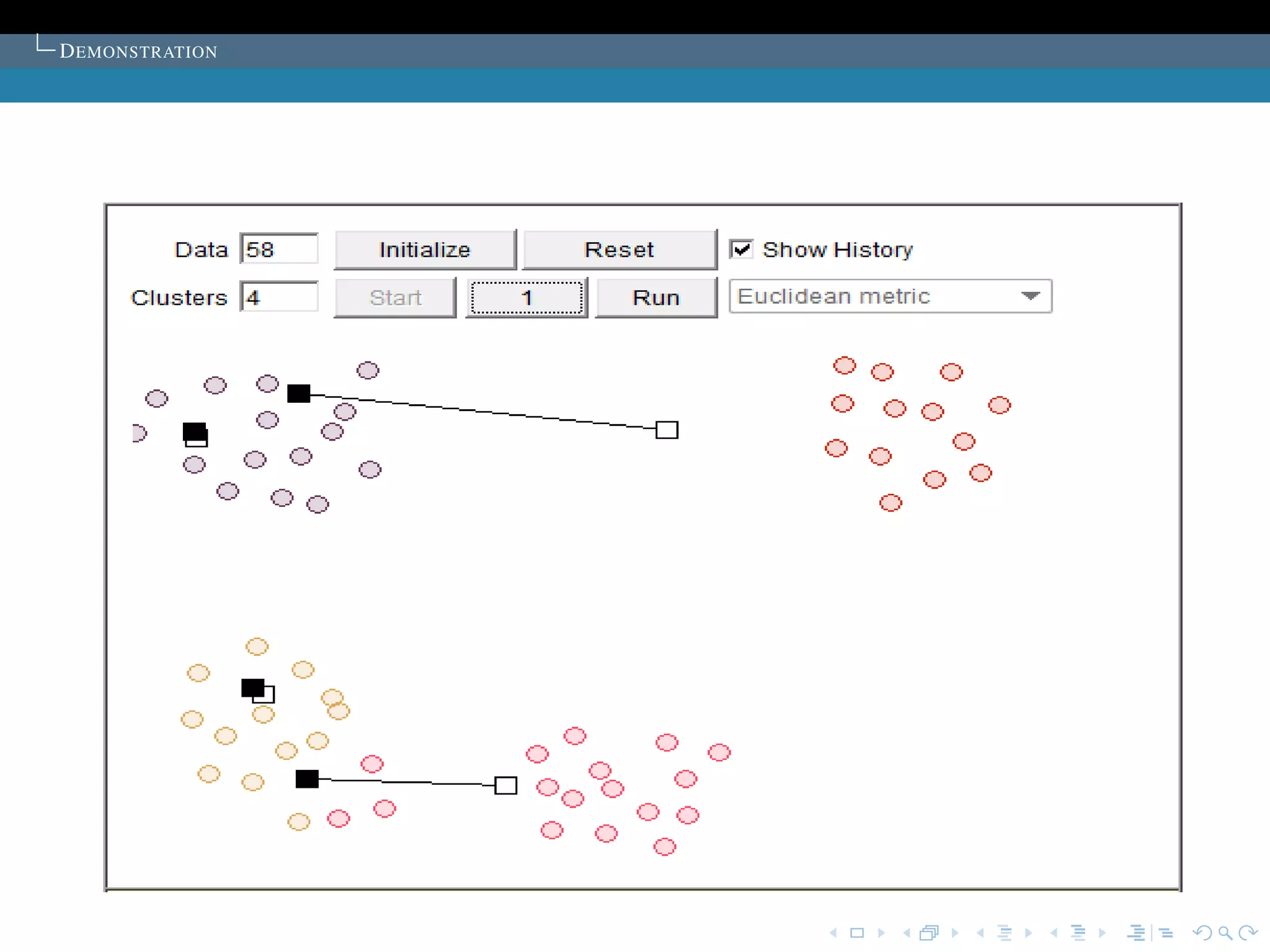
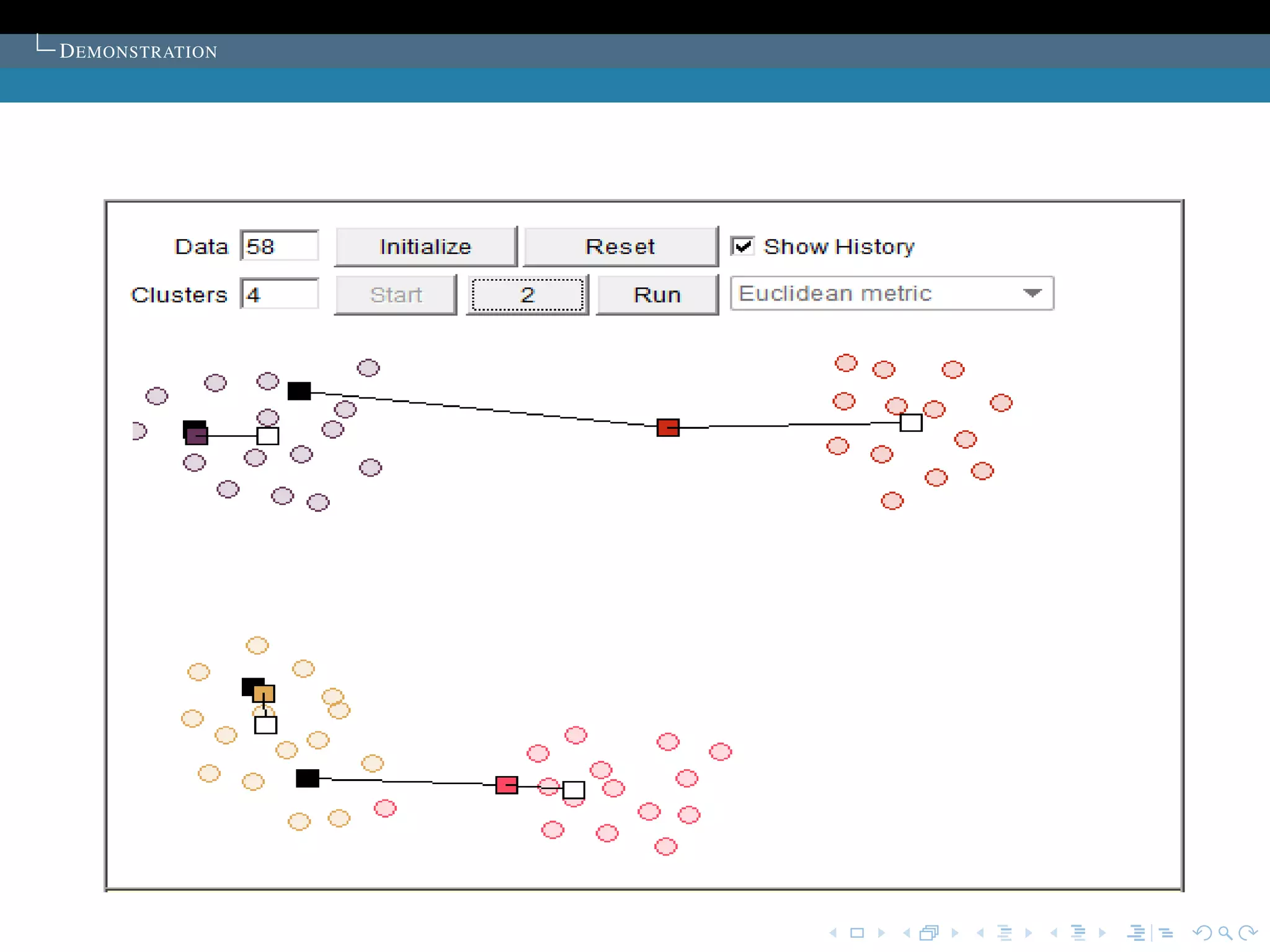
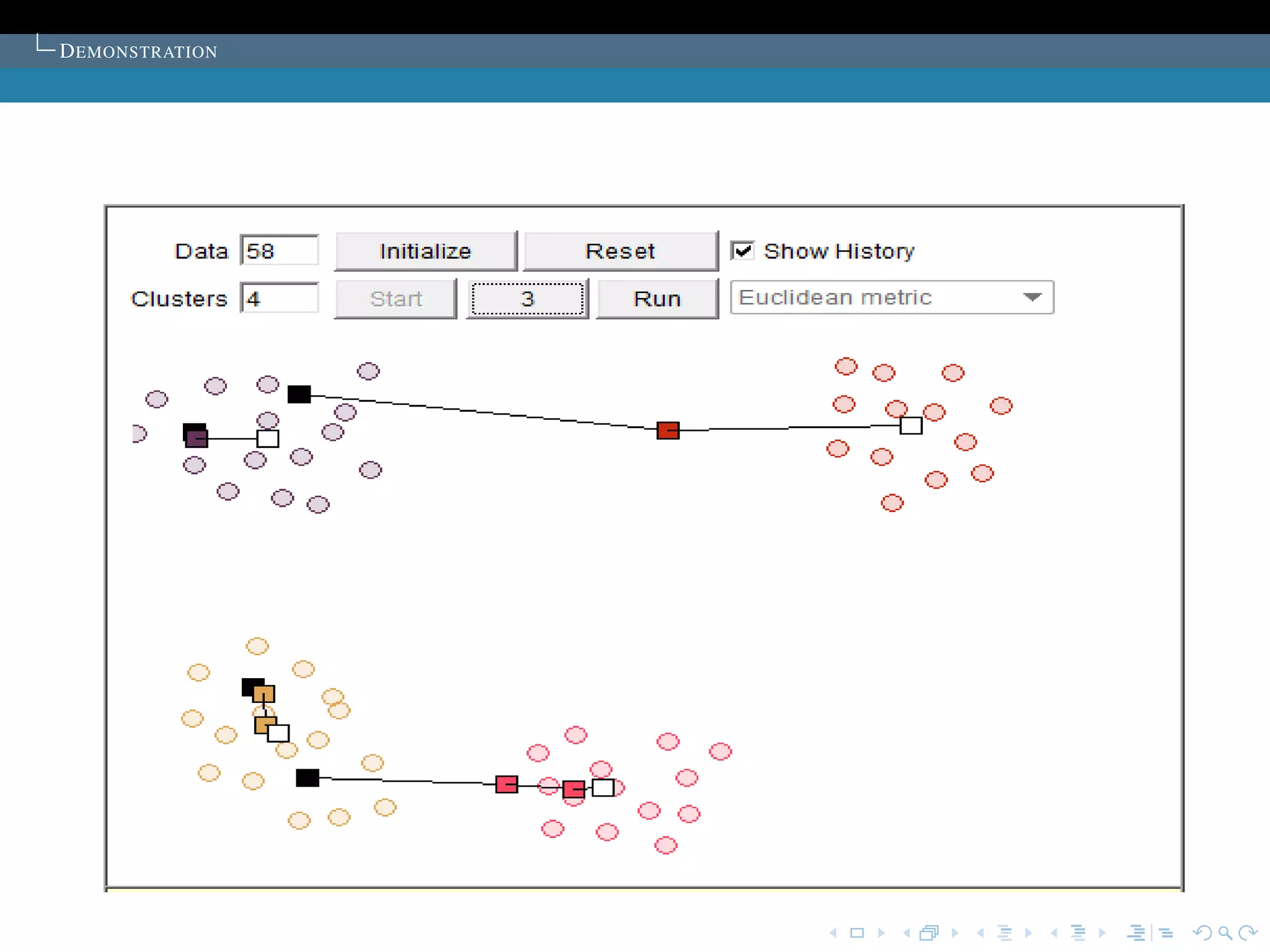
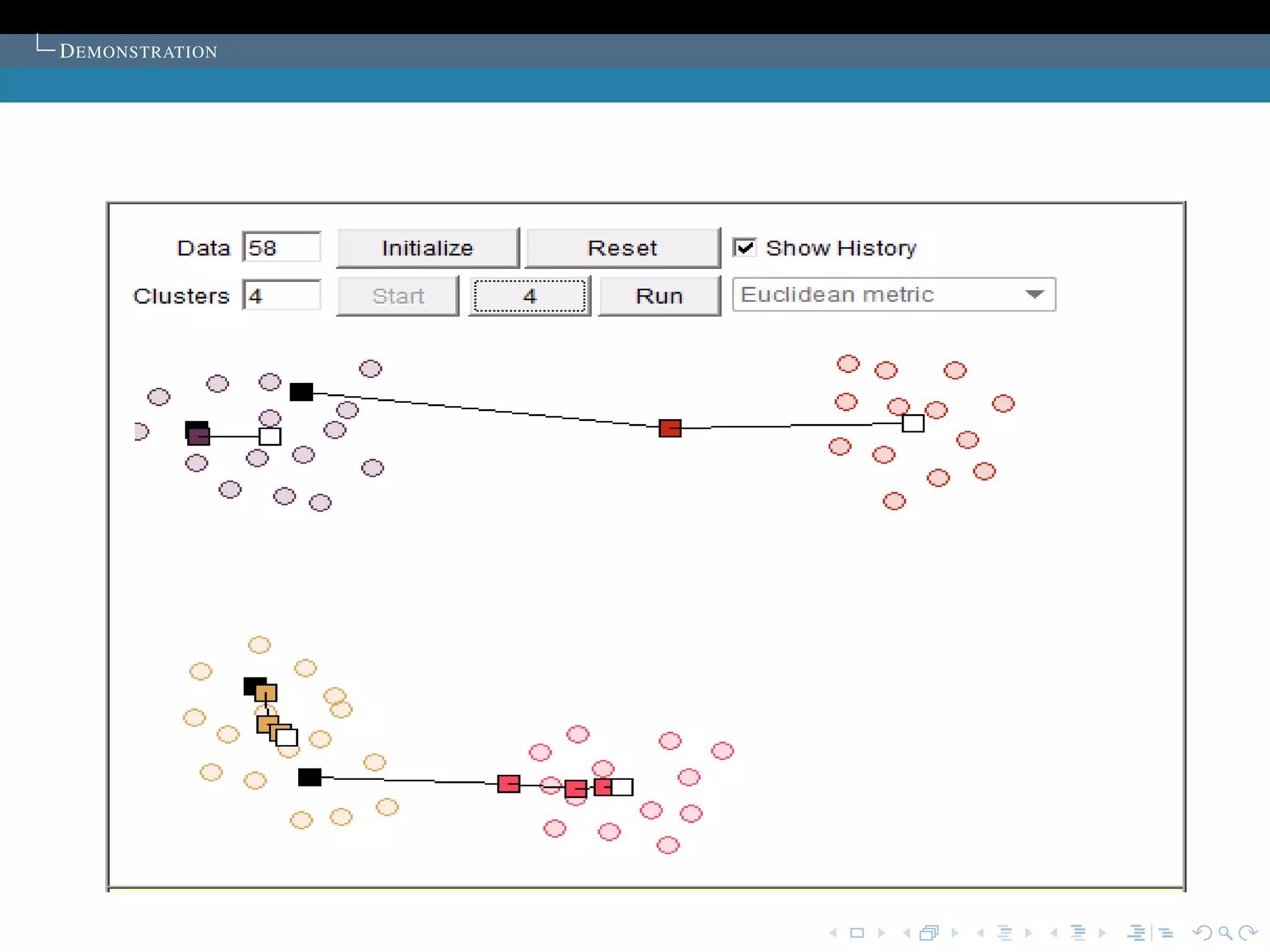
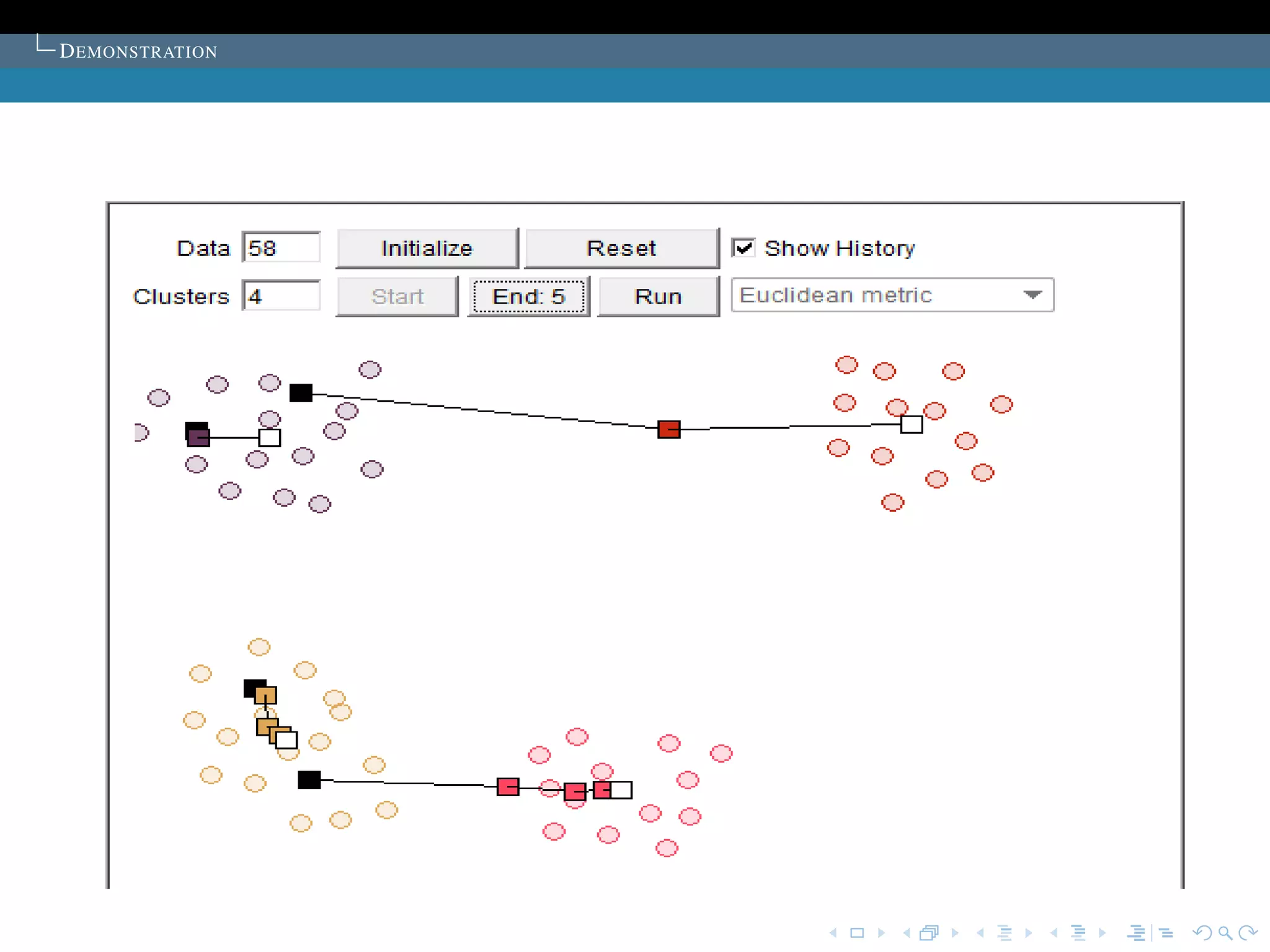
The document describes the k-means clustering algorithm. It introduces clustering and its aim to divide data points into k clusters to minimize within-cluster sums of squares. The algorithm involves initializing cluster centers, then iteratively performing optimal transfers of points between clusters and quick transfers until convergence is reached. Optimal transfers minimize an objective function to determine the best cluster for a point, while quick transfers perform simpler transfers without minimizing the objective.

1. R EADING SEMINAR ON CLASSICS
PRESENTED BY
´
B EJI C E LINE
Article
AS 136: A K-Means Clustering Algorithm
Suggested by C. Robert

2. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

3. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

4. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

5. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

6. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

7. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

8. Plan
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

9. I NTRODUCTION
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

10. I NTRODUCTION
P RESENTATION OF THE ARTICLE
AS 136: A K-Means Clustering Algorithm
Authors: J. A Hartigan and M. A. Wong
Source: Journal of the Roal Statistical Society. Series C
(Applied Statistics), Vol 28, No.1 (1979), pp.100-108
Implemented in FORTRAN

11. I NTRODUCTION
C LUSTERING
Clustering is the classical problem of dividing a data sample in
some space into a collection of disjoint groups.

12. I NTRODUCTION
T HE AIM OF THE ALGORITHM
Divide M points in N dimensions into K clusters
so that the within-cluster sum of squares is
minimized.

13. I NTRODUCTION
E XAMPLE OF APPLICATION
The algorithm is apply even on large data sets.
For example ranging from:
Market segmentation
Image processing
Geostatistics
...

14. I NTRODUCTION
E XAMPLE OF APPLICATION
M ARKET SEGMENTATION
It is necessary to segment the Customer in order to know more
precisely the needs and expectations of each group.
M: number of people
N: number of criterion (age, sex, social status, etc ...)
k: number of cluster
F IGURE : market segmentation

15. AGORITHM
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

16. AGORITHM
F IGURE : General Schema

17. AGORITHM
F IGURE : General Schema

18. AGORITHM
I NITIALIZATION
1 For each point point (I=1,2,...,M) find its clostest and
second clostest cluster centers, keep them in IC1(I) and
IC2(I), respectively.
2 Update the cluster centres to be the average of the points
contained within them.
3 Put all cluster in the live set.

19. AGORITHM
I NITIALIZATION
1 For each point point (I=1,2,...,M) find its clostest and
second clostest cluster centers, keep them in IC1(I) and
IC2(I), respectively.
2 Update the cluster centres to be the average of the points
contained within them.
3 Put all cluster in the live set.

20. AGORITHM
I NITIALIZATION
1 For each point point (I=1,2,...,M) find its clostest and
second clostest cluster centers, keep them in IC1(I) and
IC2(I), respectively.
2 Update the cluster centres to be the average of the points
contained within them.
3 Put all cluster in the live set.

21. AGORITHM
F IGURE : General Schema

22. AGORITHM
T HE LIVE SET
We consider each point (I=1,2,...,M), let point I be in cluster L1.
L1 is in the live set: If the cluster is updated in the quick-transfer
(QTRAN) stage.
L1 is not in the live set : otherwise, and if it has not been updated
in the last M optimal-transfer (OPTRA) steps.

23. AGORITHM
T HE LIVE SET
We consider each point (I=1,2,...,M), let point I be in cluster L1.
L1 is in the live set: If the cluster is updated in the quick-transfer
(QTRAN) stage.
L1 is not in the live set : otherwise, and if it has not been updated
in the last M optimal-transfer (OPTRA) steps.

24. AGORITHM
T HE LIVE SET
We consider each point (I=1,2,...,M), let point I be in cluster L1.
L1 is in the live set: If the cluster is updated in the quick-transfer
(QTRAN) stage.
L1 is not in the live set : otherwise, and if it has not been updated
in the last M optimal-transfer (OPTRA) steps.

25. AGORITHM
F IGURE : General Schema

26. AGORITHM
O PTIMAL - TRANSFER STAGE (OPTRA)
Compute the minimum of the quantity for all cluster L (L=L1) ,
NC(L) ∗ D(I, L)2
R2 = (1)
NC(L) + 1
NC(L): The number of points in cluster L
D(I,L): The Euclidean distance between point I and cluster L
Let L2 be the cluster with the smallest R2

27. AGORITHM
O PTIMAL - TRANSFER STAGE (OPTRA)
If:
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
≥ (2)
NC(L1) + 1 NC(L2) + 1
No reallocation
L2 is the new IC2(I)
If:
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (3)
NC(L1) + 1 NC(L2) + 1
I is allocated to cluster L2
L1 is the new IC2(I)
Cluster centres are updated to be the means of points
assigned to them
The two clusters that are involved in the transfer of point I at
this particular step are now in the live set

28. AGORITHM
O PTIMAL - TRANSFER STAGE (OPTRA)
If:
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
≥ (2)
NC(L1) + 1 NC(L2) + 1
No reallocation
L2 is the new IC2(I)
If:
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (3)
NC(L1) + 1 NC(L2) + 1
I is allocated to cluster L2
L1 is the new IC2(I)
Cluster centres are updated to be the means of points
assigned to them
The two clusters that are involved in the transfer of point I at
this particular step are now in the live set

29. AGORITHM
F IGURE : General Schema

30. AGORITHM
F IGURE : General Schema

31. AGORITHM
F IGURE : General Schema

32. AGORITHM
F IGURE : General Schema

33. AGORITHM
T HE QUICK - TRANSFER STAGE (QTRAN)
We consider each point (I=1,2,...,M) in turn
Let L1=IC1(I) and L2=IC2(I)
If
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (4)
NC(L1) + 1 NC(L2) + 1
Then, point I remains in cluster L1
Otherwise,
IC1 ↔ IC2
Update the centres of cluster L1 and L2
Its noted that transfer took place
This step is repeated until transfer take place in the last M
steps.

34. AGORITHM
T HE QUICK - TRANSFER STAGE (QTRAN)
We consider each point (I=1,2,...,M) in turn
Let L1=IC1(I) and L2=IC2(I)
If
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (4)
NC(L1) + 1 NC(L2) + 1
Then, point I remains in cluster L1
Otherwise,
IC1 ↔ IC2
Update the centres of cluster L1 and L2
Its noted that transfer took place
This step is repeated until transfer take place in the last M
steps.

35. AGORITHM
T HE QUICK - TRANSFER STAGE (QTRAN)
We consider each point (I=1,2,...,M) in turn
Let L1=IC1(I) and L2=IC2(I)
If
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (4)
NC(L1) + 1 NC(L2) + 1
Then, point I remains in cluster L1
Otherwise,
IC1 ↔ IC2
Update the centres of cluster L1 and L2
Its noted that transfer took place
This step is repeated until transfer take place in the last M
steps.

36. AGORITHM
T HE QUICK - TRANSFER STAGE (QTRAN)
We consider each point (I=1,2,...,M) in turn
Let L1=IC1(I) and L2=IC2(I)
If
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (4)
NC(L1) + 1 NC(L2) + 1
Then, point I remains in cluster L1
Otherwise,
IC1 ↔ IC2
Update the centres of cluster L1 and L2
Its noted that transfer took place
This step is repeated until transfer take place in the last M
steps.

37. AGORITHM
T HE QUICK - TRANSFER STAGE (QTRAN)
We consider each point (I=1,2,...,M) in turn
Let L1=IC1(I) and L2=IC2(I)
If
NC(L1) ∗ D(I, L1)2 NC(L2) ∗ D(I, L2)2
< (4)
NC(L1) + 1 NC(L2) + 1
Then, point I remains in cluster L1
Otherwise,
IC1 ↔ IC2
Update the centres of cluster L1 and L2
Its noted that transfer took place
This step is repeated until transfer take place in the last M
steps.

38. AGORITHM
F IGURE : General Schema

39. D EMONSTRATION
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

40. D EMONSTRATION

41. D EMONSTRATION

42. D EMONSTRATION

43. D EMONSTRATION

44. D EMONSTRATION

45. D EMONSTRATION

46. D EMONSTRATION

47. C ONVERGENCE AND T IME
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

48. C ONVERGENCE AND T IME
C ONVERGENCE
There are convergence, but the algorithm produces a clustering
which is only locally optimal!
F IGURE : A typical example of the k-means convergence to a local
optima

49. C ONVERGENCE AND T IME
T IME
The time i approximately equal to
CMNKI
C: depends on the speed of the computer (=2.1×10−5 sec
for an IBM 370/158)
M: the number of points
N: the number of dimensions
K: the number of clusters
I: the number of iterations (usually less than 10)

50. C ONSIDERABLE PROGRESS
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

51. C ONSIDERABLE PROGRESS
R ELATED ALGORITHM
AS 113: A TRANSFER ALGORITHM FOR NON - HIERARCHIAL
CLASSIFICATION
(by Banfield and Bassil in 1977)
It uses swops as well as transfer to try to overcome the
problem of local optima.
It is too expensive to use if the size of the data set is
significant.

52. C ONSIDERABLE PROGRESS
R ELATED ALGORITHM
AS 58: E UCLIDEAN CLUSTER ANALYSIS
(by Sparks in 1973)
It find a K-partition of the sample, with within-cluster sum of
squares.
Only the closest centre is used to check for possible
reallocation of the given point, it does not provide a locally
optimal solution.
A saving of about 50 per cent in time occurs in the
k-Means algorithm due to using ”live” sets and due to using
a quick- transfer stage which reduces the number of
optimal transfer iterations by a factor of 4.

53. T HE LIMITS OF THE ALGORITHM
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

54. T HE LIMITS OF THE ALGORITHM
T HE SELECTION OF THE INITIAL CLUSTER CENTRES
F IGURE : The choice of the initial cluster centres affect the final results

55. T HE LIMITS OF THE ALGORITHM
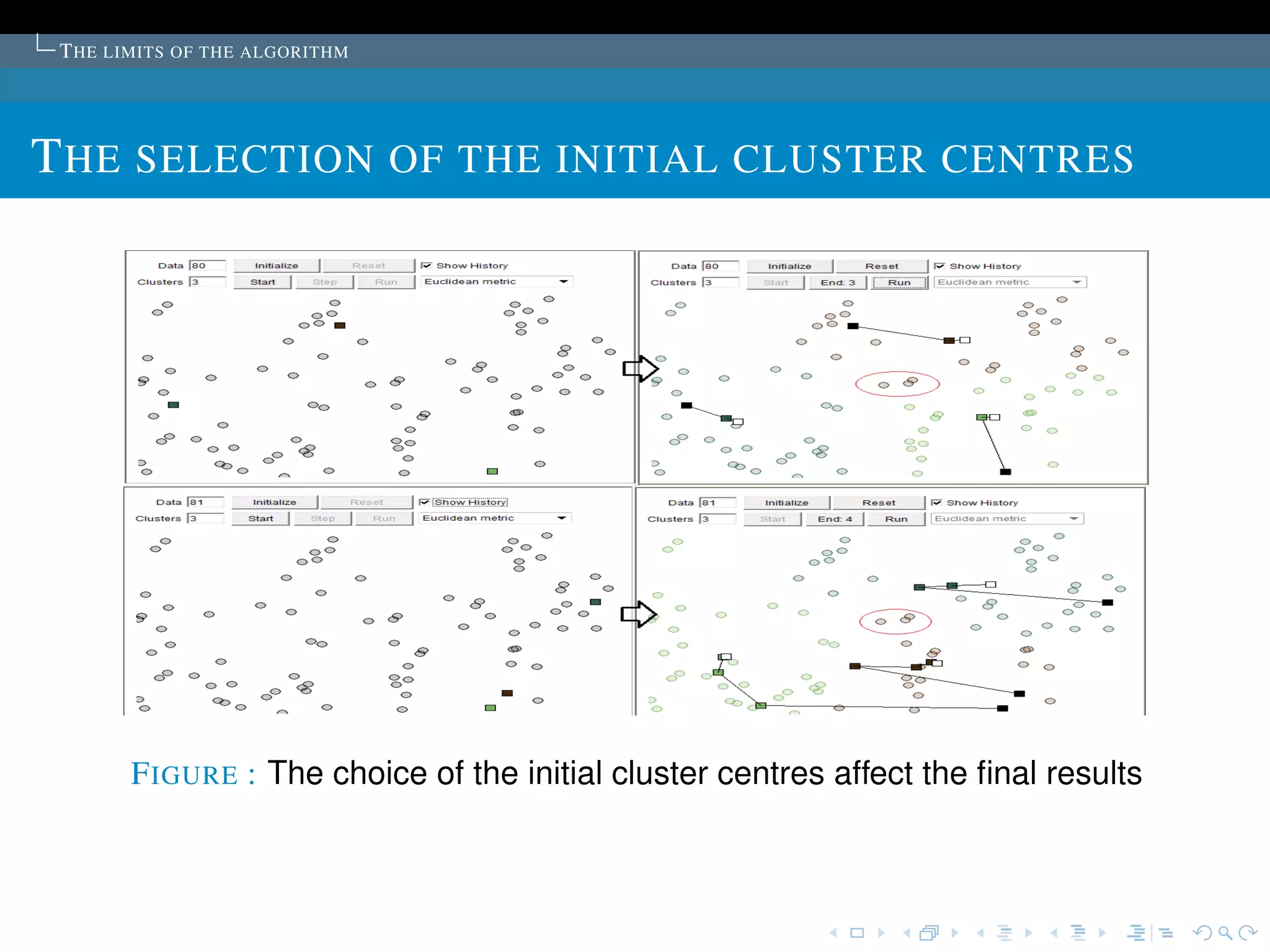
T HE SELECTION OF THE INITIAL CLUSTER CENTRES
T HE SOLUTION TO THE PROBLEM
Proposed in the article:K sample points are chosen as
the initial cluster centres.
The points are first ordered by their distances to the overall
mean of the sample. Then, for cluster L (L = 1,2, ..., K), the
1 + (L -1) * [M/K]th point is chosen to be its initial cluster
centre (it is guaranteed that no cluster will be empty).
Commonly used:The cluster centers are chosen
randomly.
The algorithm is run several time, then select the set of
cluster with minimum sum of the Squared Error.

56. T HE LIMITS OF THE ALGORITHM
T HE SELECTION OF THE NUMBER OF CLUSTERS
T HE SOLUTION TO THE PROBLEM : T HE MEAN SHIFT ALGORITHM
The mean shift is similar to K-means in that it maintains a set of
data points that are iteratively replaced by means.
But there is no need to choose the number of clusters, because
mean shift is likely to find only a few clusters if indeed only a
small number exist.

57. T HE LIMITS OF THE ALGORITHM
S ENSITIVITY TO NOISE
T HE SOLUTION TO THE PROBLEM :K- MEANS ALGORITHM
CONSIDERING WEIGHTS
This algorithm is the same as the k-mean, but each variable is
weighted to provide a lower weight to the variables affected by high
noise.
The center of cluster L:
WH(I)
C(L) = XI (5)
WHC(L)
The quantity computed:
WHC(L) ∗ D(I, L)2
R= (6)
WHC(L) − WH(I)
WH(I): the weight of each point I
WHC(L): the weight of each cluster L

58. C ONCLUSION
1 I NTRODUCTION
2 AGORITHM
3 D EMONSTRATION
4 C ONVERGENCE AND T IME
5 C ONSIDERABLE PROGRESS
6 T HE LIMITS OF THE ALGORITHM
7 C ONCLUSION

59. C ONCLUSION
C ONCLUSION
This algorithm has been a real revolution for the clustering
methods:It produces good results and a high speed of
convergence.
This algorithm possesses flaws, but many algorithms
implemented today are arising from it.

60. C ONCLUSION
R EFERENCES
J. A. Hartigan and M. A.Wong (1979) Algorithm AS 136: A
K-Means Clustering Algorithm. Appl.Statist., 28, 100-108.
http://home.dei.polimi.it/matteucc/
Clustering/tutorial_html/AppletKM.html
http:
//en.wikipedia.org/wiki/K-means_clustering

61. Thank you for your attention !!!
Retour.