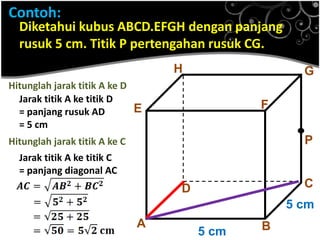
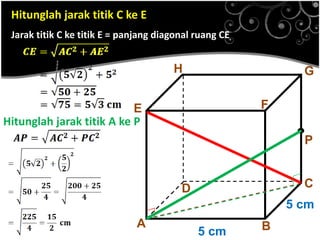
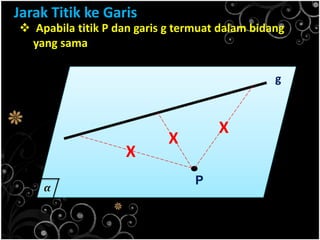
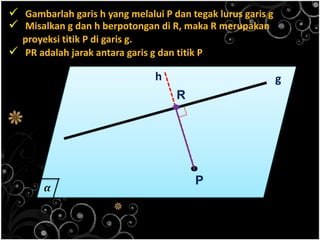
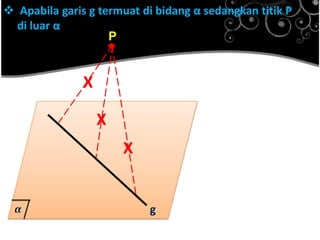
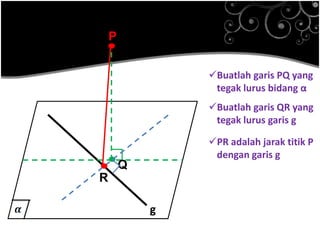
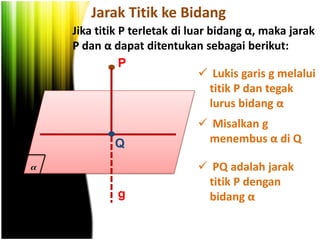
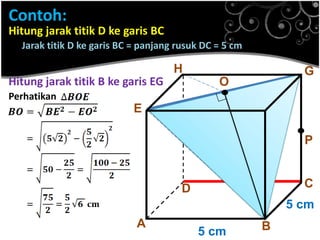
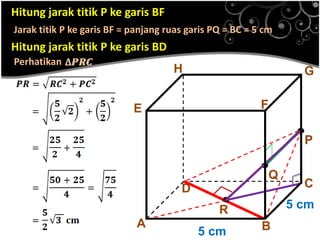
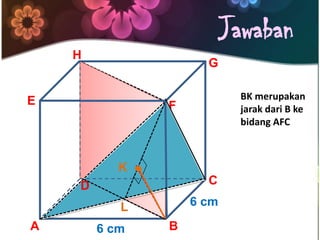
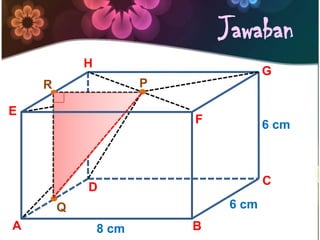
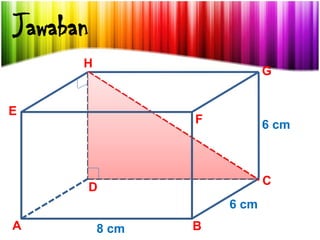
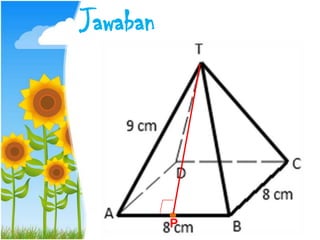
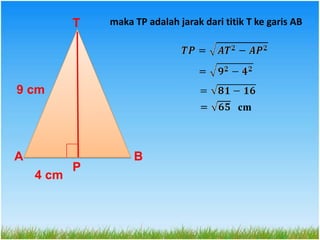
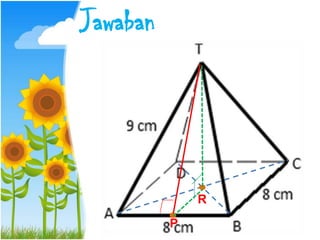
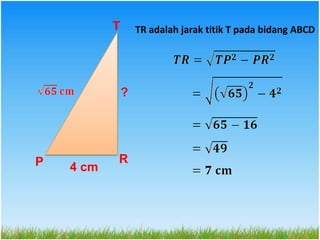
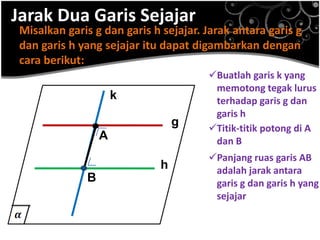
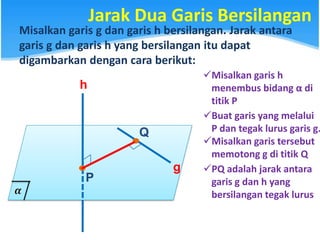
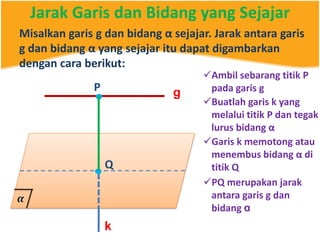
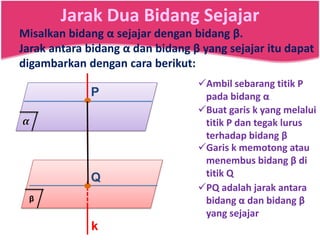
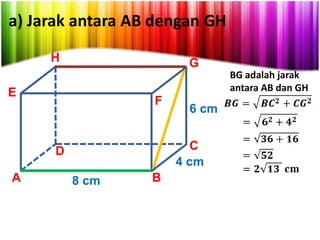
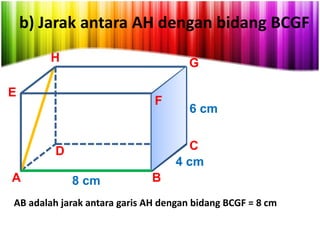
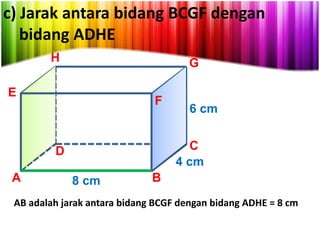
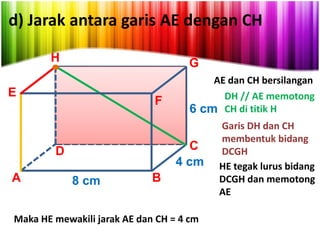
Dokumen ini menjelaskan konsep jarak dalam geometri ruang, termasuk jarak antara titik, garis, dan bidang. Metode perhitungan jarak serta contoh soal yang melibatkan bangun ruang seperti kubus dan limas disertakan untuk memperjelas konsep tersebut. Selain itu, juga dibahas cara menentukan jarak antara dua garis sejajar dan bersilangan.

1. MENENTUKAN JARAK
PADA BANGUN RUANG

2. Materi Ajar
Jarak Titik ke Titik
Jarak Titik ke Garis
Jarak Titik ke Bidang

3. Konsep Jarak dalam Geometri Bidang
Jarak Titik ke Titik
Jarak titik A ke titik B digambarkan dengan
cara menghubungkan titik A dan titik B
dengan ruas garis AB
.
.
( x1 , y1)
( x2 , y2)
A
Bd

4. Jarak Titik ke Garis
Jarak titik P ke garis g
digambarkan dengan cara
membuat garis dari titik P
dan tegak lurus ke garis g
.P
g
( x1 , y1)
d

5. Konsep Jarak dalam Geometri Ruang
Jarak Titik ke Titik
Jarak titik A ke titik B dalam suatu ruang dapat
digambarkan dengan cara menghubungkan titik A
dengan titik B dengan ruas garis AB.
.A
.B
d

6. Contoh:
Diketahui kubus ABCD.EFGH dengan panjang
rusuk 5 cm. Titik P pertengahan rusuk CG.
A B
CD
E F
GH
5 cm
5 cm
Hitunglah jarak titik A ke D
Jarak titik A ke titik D
= panjang rusuk AD
= 5 cm
Hitunglah jarak titik A ke C
Jarak titik A ke titik C
= panjang diagonal AC
.P

7. Hitunglah jarak titik C ke E
A B
CD
E F
GH
5 cm
5 cm
.P
Jarak titik C ke titik E = panjang diagonal ruang CE
Hitunglah jarak titik A ke P

8. Jarak Titik ke Garis
 Apabila titik P dan garis g termuat dalam bidang
yang sama
.P
g
X
X
X

9.  Gambarlah garis h yang melalui P dan tegak lurus garis g
.P
gh
 Misalkan g dan h berpotongan di R, maka R merupakan
proyeksi titik P di garis g.
.R
 PR adalah jarak antara garis g dan titik P

10.  Apabila garis g termuat di bidang α sedangkan titik P
di luar α
.P
g
X
X
X

11. .P
g
Buatlah garis PQ yang
tegak lurus bidang α
Buatlah garis QR yang
tegak lurus garis g
.Q
PR adalah jarak titik P
dengan garis g
.R

12. Jarak Titik ke Bidang
Jika titik P terletak di luar bidang α, maka jarak
P dan α dapat ditentukan sebagai berikut:
.P
 Lukis garis g melalui
titik P dan tegak
lurus bidang α
g
 Misalkan g
menembus α di Q.Q
 PQ adalah jarak
titik P dengan
bidang α

13. Contoh:
A B
CD
E F
GH
5 cm
5 cm
.P
Hitung jarak titik D ke garis BC
Jarak titik D ke garis BC = panjang rusuk DC = 5 cm
Hitung jarak titik B ke garis EG O
.Perhatikan

14. A B
CD
E F
GH
5 cm
5 cm
Hitung jarak titik P ke garis BF
.P
.Q
Jarak titik P ke garis BF = panjang ruas garis PQ = BC = 5 cm
Hitung jarak titik P ke garis BD
R
.
Perhatikan

15. LATIHAN SOAL
Diketahui kubus ABCD.EFGH
dengan panjang rusuk 6 cm.
Hitung jarak titik B ke bidang
AFC.

16. Jawaban
A B
C
E F
G
H
L
K .
D
6 cm
6 cm
BK merupakan
jarak dari B ke
bidang AFC

17. Perhatikan
L B
F
K
α
6 cm
FB = 6 cm
Jadi, jarak titik B ke bidang AFC adalah

18. LATIHAN SOAL
Balok ABCD.EFGH memiliki ukuran panjang 8 cm,
lebar 6 cm, dan tinggi 6 cm. Misalkan titik P
merupakan perpotongan diagonal bidang FH dan
EG, titik R terletak di pertengahan ruas garis EH
dan titik Q di pertengahan ruas garis AD.
a. Tentukan jarak antara titik P dan garis AD.
b. Tentukan jarak antara titik C dan garis EH

19. Jawaban
P
..
.
R
Q
A B
C
D
E
F
G
H
8 cm
6 cm
6 cm

20. Jarak antara titik P dan garis AD
= panjang ruas garis PQ

21. Jawaban
A B
C
D
E
F
G
H
8 cm
6 cm
6 cm

22. LATIHAN SOAL
Diketahui limas segiempat beraturan
T.ABCD dengan panjang rusuk bidang alas
AB = 8 cm dan panjang rusuk sisi TA = 9 cm.
a) Hitunglah jarak titik T ke rusuk alas AB.
b) Hitunglah jarak titik puncak T ke bidang
alas ABCD.

23. Jawaban
P
.

24. BA
T
P
maka TP adalah jarak dari titik T ke garis AB
cm
9 cm
4 cm

25. Jawaban
R
.
P
.

26. TR adalah jarak titik T pada bidang ABCD
P
T
4 cm
R
?

27. Materi Ajar
Jarak Garis ke Garis
Jarak Garis ke Bidang
Jarak Bidang ke Bidang

28. Jarak Dua Garis Sejajar
Misalkan garis g dan garis h sejajar. Jarak antara garis g
dan garis h yang sejajar itu dapat digambarkan dengan
cara berikut:
g
h
Buatlah garis k yang
memotong tegak lurus
terhadap garis g dan
garis h
k
Titik-titik potong di A
dan BA
B
Panjang ruas garis AB
adalah jarak antara
garis g dan garis h yang
sejajar
.
.

29. Jarak Dua Garis Bersilangan
Misalkan garis g dan garis h bersilangan. Jarak antara
garis g dan garis h yang bersilangan itu dapat
digambarkan dengan cara berikut:
h
g
Misalkan garis h
menembus bidang α di
titik P
P
Buat garis yang melalui
P dan tegak lurus garis g.
Misalkan garis tersebut
memotong g di titik Q
.
Q
.
PQ adalah jarak antara
garis g dan h yang
bersilangan tegak lurus

30. Jarak Garis dan Bidang yang Sejajar
Misalkan garis g dan bidang α sejajar. Jarak antara garis
g dan bidang α yang sejajar itu dapat digambarkan
dengan cara berikut:
g
Ambil sebarang titik P
pada garis gP
. Buatlah garis k yang
melalui titik P dan tegak
lurus bidang α
Q.
k
Garis k memotong atau
menembus bidang α di
titik Q
PQ merupakan jarak
antara garis g dan
bidang α

31. Jarak Dua Bidang Sejajar
Misalkan bidang α sejajar dengan bidang β.
Jarak antara bidang α dan bidang β yang sejajar itu dapat
digambarkan dengan cara berikut:
β
Ambil sebarang titik P
pada bidang αP
Buat garis k yang melalui
titik P dan tegak lurus
terhadap bidang β
.
Q
.
Garis k memotong atau
menembus bidang β di
titik Q
k
PQ adalah jarak antara
bidang α dan bidang β
yang sejajar

32. LATIHAN SOAL
ABCD.EFGH memiliki panjang 8 cm, lebar 4
cm, dan tinggi 6 cm. Tentukan jarak antara:
a) AB dengan GH
b) AH dengan bidang BCGF
c) Bidang BCGF dengan bidang ADHE
d) Garis AE dengan CH

33. a) Jarak antara AB dengan GH
A B
CD
E
F
G
8 cm
4 cm
6 cm
H
BG adalah jarak
antara AB dan GH

34. b) Jarak antara AH dengan bidang BCGF
A B
CD
E
G
8 cm
4 cm
6 cm
H
F
AB adalah jarak antara garis AH dengan bidang BCGF = 8 cm

35. c) Jarak antara bidang BCGF dengan
bidang ADHE
A B
CD
E
G
8 cm
4 cm
6 cm
H
F
AB adalah jarak antara bidang BCGF dengan bidang ADHE = 8 cm

36. d) Jarak antara garis AE dengan CH
A B
CD
E
G
8 cm
4 cm
6 cm
H
AE dan CH bersilangan
DH // AE memotong
CH di titik H
Garis DH dan CH
membentuk bidang
DCGH
F
.
HE tegak lurus bidang
DCGH dan memotong
AE
Maka HE mewakili jarak AE dan CH = 4 cm

37. SELAMAT
BELAJAR