Tiga kalimat ringkasan dokumen tersebut adalah:
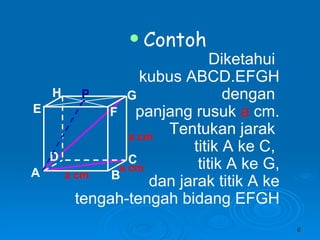
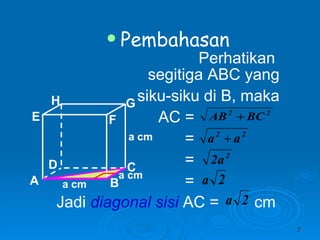
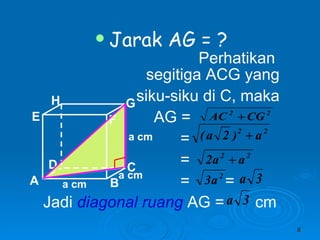
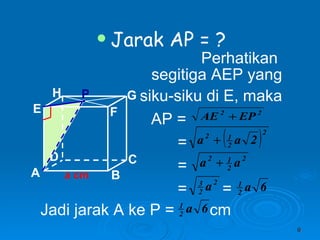
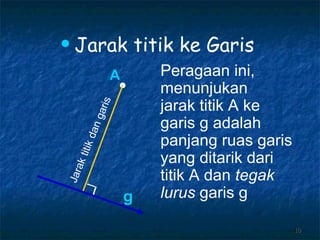
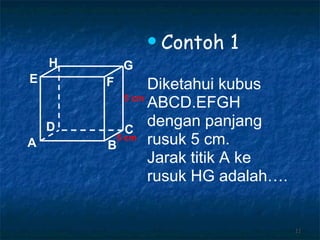
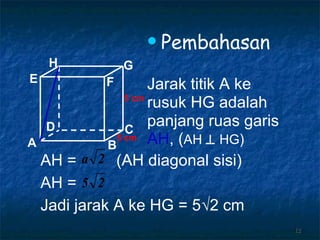
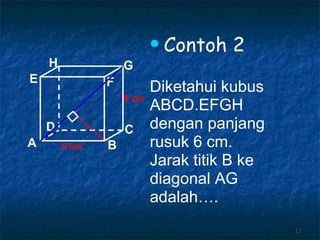
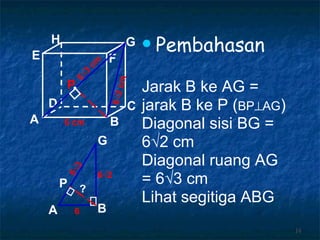
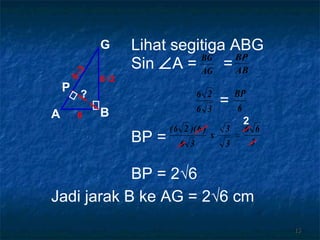
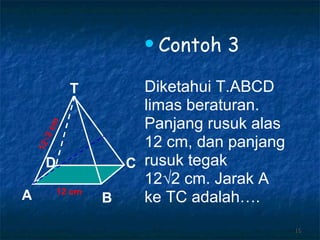
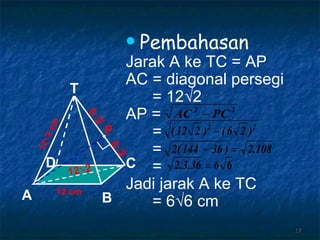
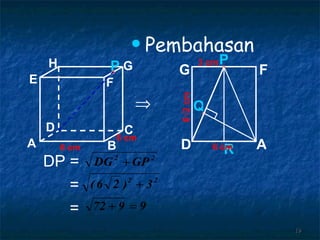
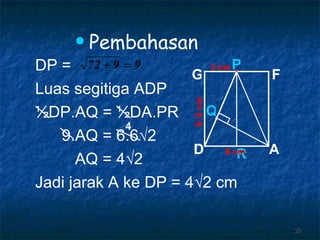
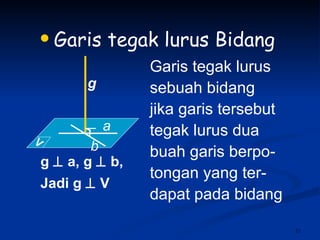
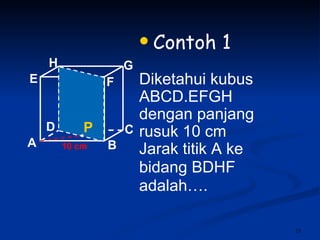
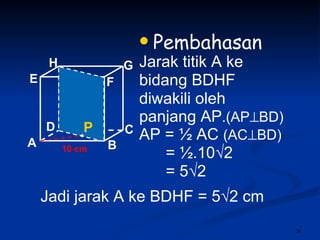
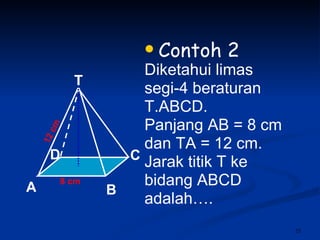
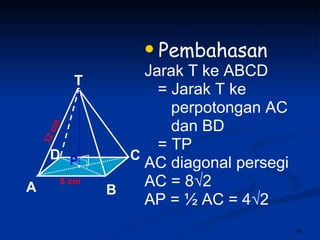
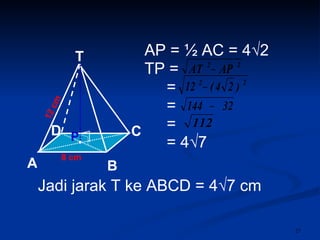
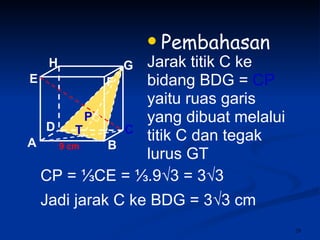
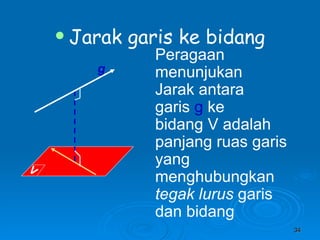
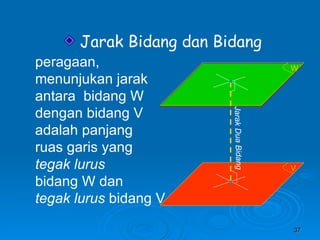
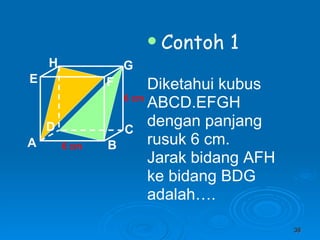
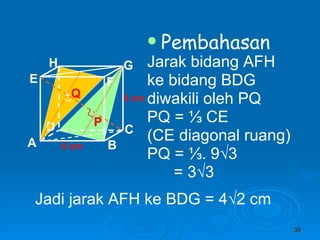
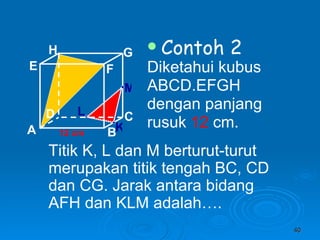
Dokumen tersebut membahas tentang dimensi tiga khususnya jarak antara berbagai unsur ruang seperti titik, garis, dan bidang. Jarak didefinisikan sebagai panjang garis yang menghubungkan unsur-unsur tersebut secara tegak lurus. Contoh perhitungan jarak antara berbagai unsur ruang pada kubus dan limas segi empat beraturan disajikan beserta penjelasann
Berisikan materi serta contoh sola mengenai jarak titik ke titik, titik ke garis, titik ke bidang, dua garis yang sejajar, dua garis yang bersilangan, garis dan bidang serta dua bidang yang sejajar..
Berisikan materi serta contoh sola mengenai jarak titik ke titik, titik ke garis, titik ke bidang, dua garis yang sejajar, dua garis yang bersilangan, garis dan bidang serta dua bidang yang sejajar..
Membahas tentang jarak titik pada bangun ruang
- Titik ke Titik
- Tititk ke Garis
- Titik ke Bidang
Di lengkapi dengan contoh soal untuk lebih memahami isi materi
Media Pembelajaran SMA tentang dimnsi tiga yang mana masih banyak siswa yang blum begitu mudah untuk memahami dan mengerjakan.
untuk belajar silahkan pelajari melalui media pembelajaran tersebut.
Matkul Kapita Selekta IV - materi Geometri Dimensi Tiga
semoga bermanfaat :)
semoga dapat membantu tugas dan pekerjaan kalian, sobat :D amiinn... untuk file ppt- nya anda bisa hubungi saya di vhannyfebian@yahoo.co.id
Membahas tentang jarak titik pada bangun ruang
- Titik ke Titik
- Tititk ke Garis
- Titik ke Bidang
Di lengkapi dengan contoh soal untuk lebih memahami isi materi
Media Pembelajaran SMA tentang dimnsi tiga yang mana masih banyak siswa yang blum begitu mudah untuk memahami dan mengerjakan.
untuk belajar silahkan pelajari melalui media pembelajaran tersebut.
Matkul Kapita Selekta IV - materi Geometri Dimensi Tiga
semoga bermanfaat :)
semoga dapat membantu tugas dan pekerjaan kalian, sobat :D amiinn... untuk file ppt- nya anda bisa hubungi saya di vhannyfebian@yahoo.co.id
Assemble the Right Team to Get the Most out of Marketing Automation
Is your marketing automation platform a tool for good or evil? Learn how the right team makes all the difference in your automated marketing efforts. This joint webcast with Marketo and MarketStar will explore the make-up of the team that can strategize, design, and execute your automated marketing campaigns, and turn your leads into clients.
Webinar: http://bit.ly/15ND9aN
ActivateTo — инструмент, который помогает организовать удобный процесс продажи товаров и услуг посредством кодов активации. ActivateTo предлагает своим пользователям:
— Безопасность. Защищённая архитектура ядра PaySto делает инструмент стабильным и безопасным как для плательщика, так и для получателя.
— Стоимость. Регистрация бесплатна. Комиссия для магазина составляет 0%.
— Интеграция. Интерфейс проверки статуса кода является неотъемлемой частью ActivateTo. Простое подключение позволяет интегрировать ActivateTo в любую информационную систему за считанные часы.
— Гибкость. Помимо указанных областей применения, ActivateTo можно использовать для решения широкого спектра финансовых задач.
Sebuah buku foto yang berjudul Lensa Kampung Ondel-Ondelferrydmn1999
Indonesia, negara kepulauan yang kaya akan keragaman budaya, suku, dan tradisi, memiliki Jakarta sebagai pusat kebudayaan yang dinamis dan unik. Salah satu kesenian tradisional yang ikonik dan identik dengan Jakarta adalah ondel-ondel, boneka raksasa yang biasanya tampil berpasangan, terdiri dari laki-laki dan perempuan. Ondel-ondel awalnya dianggap sebagai simbol budaya sakral dan memainkan peran penting dalam ritual budaya masyarakat Betawi untuk menolak bala atau nasib buruk. Namun, seiring dengan bergulirnya waktu dan perubahan zaman, makna sakral ondel-ondel perlahan memudar dan berubah menjadi sesuatu yang kurang bernilai. Kini, ondel-ondel lebih sering digunakan sebagai hiasan atau sebagai sarana untuk mencari penghasilan. Buku foto Lensa Kampung Ondel-Ondel berfokus pada Keluarga Mulyadi, yang menghadapi tantangan untuk menjaga tradisi pembuatan ondel-ondel warisan leluhur di tengah keterbatasan ekonomi yang ada. Melalui foto cerita, foto feature dan foto jurnalistik buku ini menggambarkan usaha Keluarga Mulyadi untuk menjaga tradisi pembuatan ondel-ondel sambil menghadapi dilema dalam mempertahankan makna budaya di tengah perubahan makna dan keterbatasan ekonomi keluarganya. Buku foto ini dapat menggambarkan tentang bagaimana keluarga tersebut berjuang untuk menjaga warisan budaya mereka di tengah arus modernisasi.
UNTUK DOSEN Materi Sosialisasi Pengelolaan Kinerja Akademik DosenAdrianAgoes9
sosialisasi untuk dosen dalam mengisi dan memadankan sister akunnya, sehingga bisa memutakhirkan data di dalam sister tersebut. ini adalah untuk kepentingan jabatan akademik dan jabatan fungsional dosen. penting untuk karir dan jabatan dosen juga untuk kepentingan akademik perguruan tinggi terkait.
3. Setelah menyaksikan tayangan ini anda dapat Menentukan jarak antara unsur-unsur dalam ruang dimensi tiga
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15. Lihat segitiga ABG Sin A = = = BP = BP = 2√6 ? Jadi jarak B ke AG = 2 √6 cm 2 A B G P 6 √3 6 6 √2
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27. AP = ½ AC = 4√2 TP = = = = = 4√7 Jadi jarak T ke ABCD = 4 √7 cm 8 cm T C A B D 12 cm P
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42. 12 cm BDG ke C juga 4√3 Jarak BDG ke KLM = jarak KLM ke C = ½.4√3 = 2√3 K L M Jadi jarak AFH ke KLM = jarak AFH ke BDG + jarak BDG ke KLM = 4√3 + 2√3 = 6√3 cm A B C D H E F G
