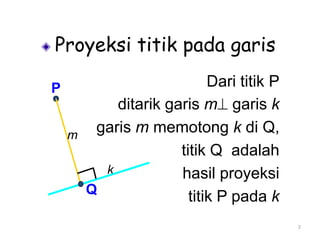
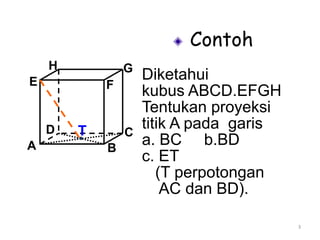
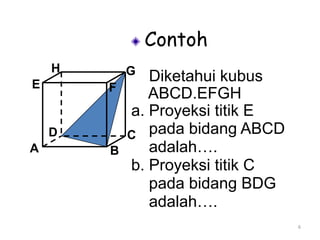
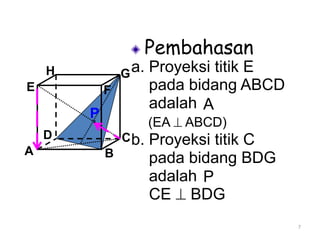
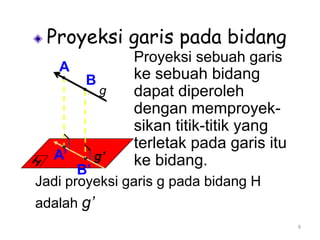
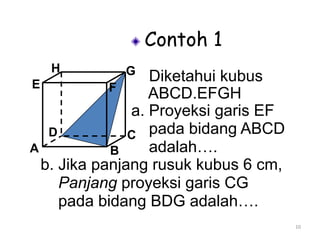
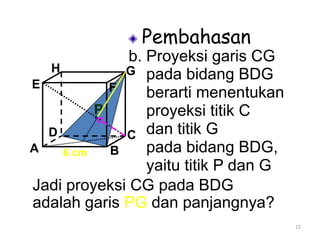
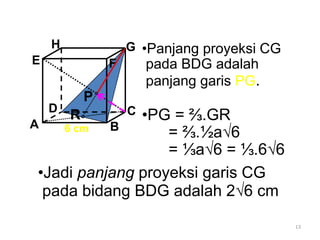
Dokumen ini membahas tentang proyeksi titik, garis, dan bidang pada bangun ruang datar dan bangun ruang. Proyeksi titik pada garis adalah titik potong garis proyeksi dari titik tersebut ke garis target. Proyeksi titik pada bidang adalah titik potong garis proyeksi dari titik ke bidang target. Proyeksi garis pada bidang didefinisikan sebagai garis hasil proyeksi setiap titik pada garis asal ke bidang target

1. Proyeksi Pada Bangun
Ruang:
proyeksi titik pada garis
proyeksi titik pada bidang
proyeksi garis pada bidang

2. 2
Proyeksi titik pada garis
Dari titik P
ditarik garis m garis k
garis m memotong k di Q,
titik Q adalah
hasil proyeksi
titik P pada k
P
Q
k
m

3. 3
Contoh
Diketahui
kubus ABCD.EFGH
Tentukan proyeksi
titik A pada garis
a. BC b.BD
c. ET
(T perpotongan
AC dan BD).
A B
CD
H
E F
G
T

4. 4
Pembahasan
Proyeksi titik A pada
a. BC adalah titik
b. BD adalah titik
c. ET adalah titik
A B
CD
H
E F
G
T
B
T
A’
A’
(AC ET)
(AB BC)
(AC BD)

5. 5
Proyeksi Titik pada Bidang
Dari titik P
di luar bidang H
ditarik garis g H.
Garis g menembus
bidang H di titik P’.
Titik P’ adalah
proyeksi titik P
di bidang H
P
P’
g

6. 6
Contoh
Diketahui kubus
ABCD.EFGH
a. Proyeksi titik E
pada bidang ABCD
adalah….
b. Proyeksi titik C
pada bidang BDG
adalah….
A B
CD
H
E F
G

7. 7
Pembahasan
a. Proyeksi titik E
pada bidang ABCD
adalah
b. Proyeksi titik C
pada bidang BDG
adalah
CE BDG
A B
CD
H
E F
G
(EA ABCD)
A
P
P

8. 8
Proyeksi garis pada bidang
Proyeksi sebuah garis
ke sebuah bidang
dapat diperoleh
dengan memproyek-
sikan titik-titik yang
terletak pada garis itu
ke bidang.
A
A’
g
Jadi proyeksi garis g pada bidang H
adalah g’
B
B’
g’

9. 9
Fakta-fakta
1. Proyeksi garis pada bidang
umumnya berupa garis
2. Jika garis h maka
proyeksi garis h pada bidang
berupa titik.
3. Jika garis g // bidang maka
g’ yaitu proyeksi garis g pada
dan sejajar garis g

10. 10
Contoh 1
Diketahui kubus
ABCD.EFGH
a. Proyeksi garis EF
pada bidang ABCD
adalah….A B
CD
H
E F
G
b. Jika panjang rusuk kubus 6 cm,
Panjang proyeksi garis CG
pada bidang BDG adalah….

11. 11
Pembahasan
a. Proyeksi garis EF
pada bidang ABCD
berarti menentukan
proyeksi titik E dan F
pada bidang ABCD,
yaitu titik A dan B
A B
CD
H
E F
G
Jadi proyeksi EF pada ABCD
adalah garis AB

12. 12
Pembahasan
b. Proyeksi garis CG
pada bidang BDG
berarti menentukan
proyeksi titik C
dan titik G
pada bidang BDG,
yaitu titik P dan G
A B
CD
H
E F
G
Jadi proyeksi CG pada BDG
adalah garis PG dan panjangnya?
P
6 cm

13. 13
A B
CD
H
E F
G •Panjang proyeksi CG
pada BDG adalah
panjang garis PG.
•PG = ⅔.GR
= ⅔.½a√6
= ⅓a√6 = ⅓.6√6
P
R
•Jadi panjang proyeksi garis CG
pada bidang BDG adalah 2√6 cm
6 cm

14. 14
Contoh 2
Diketahui limas
beraturanT.ABCD
dengan panjang AB
= 16 cm, TA = 18 cm
Panjang proyeksi TA
pada bidang ABCD
adalah….
T
A
D C
B16 cm

15. 15
Pembahasan
Proyeksi TA
pada bidang ABCD
adalah AT’.
Panjang AT’= ½AC
= ½.16√2
= 8√2
T
A
D C
B16 cm
T’
Jadi panjang proyeksi TA pada
bidang ABCD adalah 8√2 cm