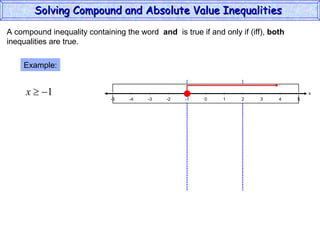
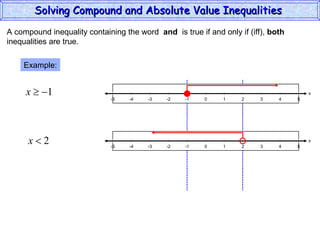
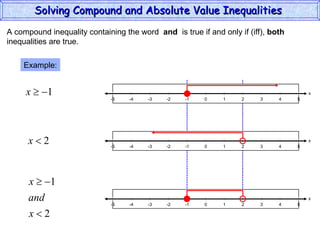
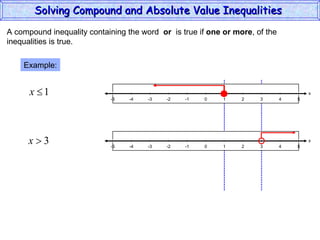
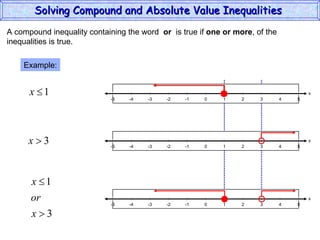
This document discusses how to solve compound and absolute value inequalities. It defines compound inequalities as consisting of two inequalities joined by "and" or "or". To solve them, each part must be solved separately. Absolute value inequalities are interpreted as distances on a number line. |a| < b is solved as -b < a < b, while |a| > b is solved as a < -b or a > b.

1. Solving Compound and Absolute Value Inequalities

2. Solving Compound and Absolute Value Inequalities Vocabulary 1) compound inequality 2) intersection 3) union Solve compound inequalities. Solve absolute value inequalities.

3. A compound inequality consists of two inequalities joined by the word and or the word or . Solving Compound and Absolute Value Inequalities

4. A compound inequality consists of two inequalities joined by the word and or the word or . To solve a compound inequality, you must solve each part of the inequality. Solving Compound and Absolute Value Inequalities

5. A compound inequality consists of two inequalities joined by the word and or the word or . To solve a compound inequality, you must solve each part of the inequality. The graph of a compound inequality containing the word “ and ” is the intersection of the solution set of the two inequalities. Solving Compound and Absolute Value Inequalities

6. A compound inequality divides the number line into three separate regions. Solving Compound and Absolute Value Inequalities

7. A compound inequality divides the number line into three separate regions. Solving Compound and Absolute Value Inequalities x y z

8. Solving Compound and Absolute Value Inequalities x A compound inequality divides the number line into three separate regions. The solution set will be found: in the blue (middle) region y z

9. Solving Compound and Absolute Value Inequalities x A compound inequality divides the number line into three separate regions. The solution set will be found: in the blue (middle) region y z or in the red (outer) regions.

10. A compound inequality containing the word and is true if and only if (iff), both inequalities are true. Solving Compound and Absolute Value Inequalities

11. A compound inequality containing the word and is true if and only if (iff), both inequalities are true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

12. A compound inequality containing the word and is true if and only if (iff), both inequalities are true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

13. A compound inequality containing the word and is true if and only if (iff), both inequalities are true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

14. A compound inequality containing the word and is true if and only if (iff), both inequalities are true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

15. A compound inequality containing the word or is true if one or more , of the inequalities is true. Solving Compound and Absolute Value Inequalities

16. A compound inequality containing the word or is true if one or more , of the inequalities is true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

17. A compound inequality containing the word or is true if one or more , of the inequalities is true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

18. A compound inequality containing the word or is true if one or more , of the inequalities is true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

19. A compound inequality containing the word or is true if one or more , of the inequalities is true. Example: Solving Compound and Absolute Value Inequalities x 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

20. A compound inequality divides the number line into three separate regions. The solution set will be found: in the blue (middle) region or in the red (outer) regions. Solving Compound and Absolute Value Inequalities x y z

21. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. Solving Compound and Absolute Value Inequalities

22. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. To make |a| < 4 true, you must substitute numbers for a that are fewer than 4 units from 0. Solving Compound and Absolute Value Inequalities

23. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. To make |a| < 4 true, you must substitute numbers for a that are fewer than 4 units from 0. Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

24. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. To make |a| < 4 true, you must substitute numbers for a that are fewer than 4 units from 0. Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

25. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. To make |a| < 4 true, you must substitute numbers for a that are fewer than 4 units from 0. Notice that the graph of |a| < 4 is the same as the graph a > -4 and a < 4. Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

26. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. To make |a| < 4 true, you must substitute numbers for a that are fewer than 4 units from 0. Notice that the graph of |a| < 4 is the same as the graph a > -4 and a < 4. All of the numbers between -4 and 4 are less than 4 units from 0. The solution set is { a | -4 < a < 4 } Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

27. Solve an Absolute Value Inequality (<) You can interpret |a| < 4 to mean that the distance between a and 0 on a number line is less than 4 units. To make |a| < 4 true, you must substitute numbers for a that are fewer than 4 units from 0. Notice that the graph of |a| < 4 is the same as the graph a > -4 and a < 4. All of the numbers between -4 and 4 are less than 4 units from 0. The solution set is { a | -4 < a < 4 } Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 For all real numbers a and b , b > 0, the following statement is true: If |a| < b then, -b < a < b

28. A compound inequality divides the number line into three separate regions. The solution set will be found: in the blue (middle) region or in the red (outer) regions. Solving Compound and Absolute Value Inequalities x y z

29. Solve an Absolute Value Inequality (>) Solving Compound and Absolute Value Inequalities

30. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. Solving Compound and Absolute Value Inequalities

31. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. To make |a| > 2 true, you must substitute numbers for a that are more than 2 units from 0. Solving Compound and Absolute Value Inequalities

32. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. To make |a| > 2 true, you must substitute numbers for a that are more than 2 units from 0. Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

33. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. To make |a| > 2 true, you must substitute numbers for a that are more than 2 units from 0. Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

34. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. To make |a| > 2 true, you must substitute numbers for a that are more than 2 units from 0. Notice that the graph of |a| > 2 is the same as the graph a < -2 or a > 2. Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

35. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. To make |a| > 2 true, you must substitute numbers for a that are more than 2 units from 0. Notice that the graph of |a| > 2 is the same as the graph a < -2 or a > 2. All of the numbers not between -2 and 2 are greater than 2 units from 0. The solution set is { a | a > 2 or a < -2 } Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3

36. Solve an Absolute Value Inequality (>) You can interpret |a| > 2 to mean that the distance between a and 0 on a number line is greater than 2 units. To make |a| > 2 true, you must substitute numbers for a that are more than 2 units from 0. Notice that the graph of |a| > 2 is the same as the graph a < -2 or a > 2. All of the numbers not between -2 and 2 are greater than 2 units from 0. The solution set is { a | a > 2 or a < -2 } Solving Compound and Absolute Value Inequalities 5 -4 -2 0 2 4 -5 -3 1 5 -1 -5 3 For all real numbers a and b , b > 0, the following statement is true: If |a| > b then, a < -b or a > b

37. End of Lesson Solving Compound and Absolute Value Inequalities

38. Credits PowerPoint created by Using Glencoe’s Algebra 2 text, © 2005 Robert Fant http://robertfant.com