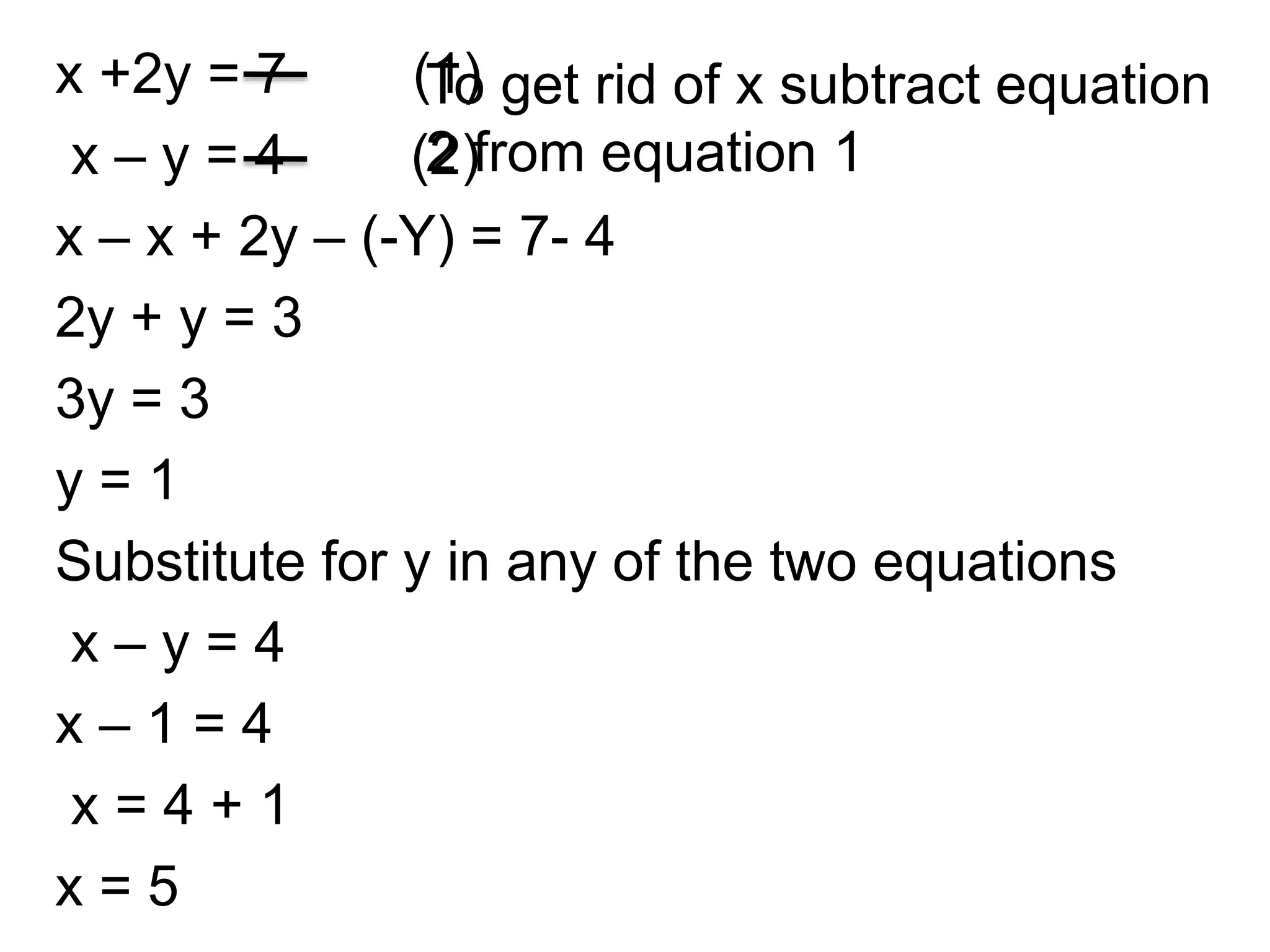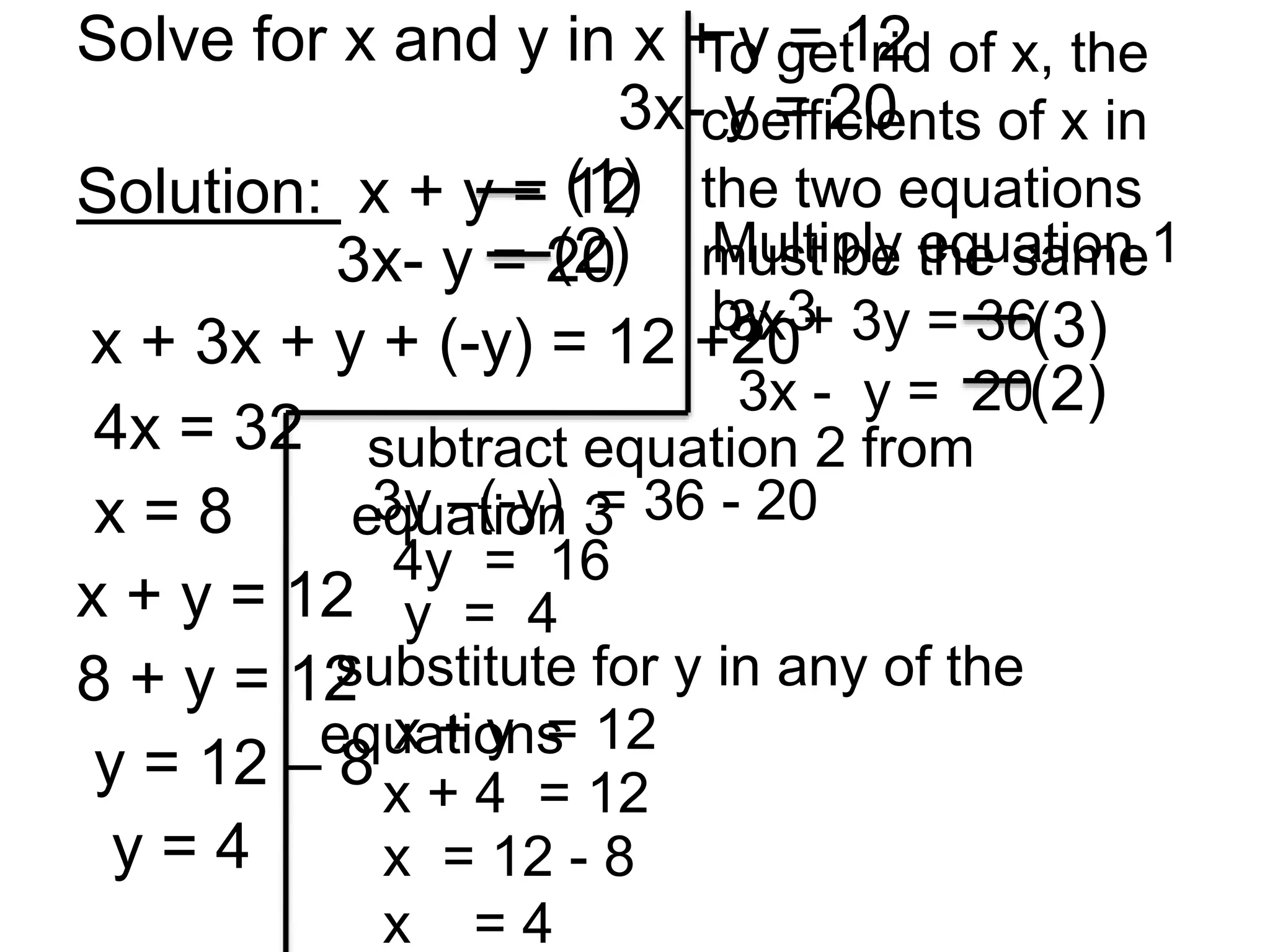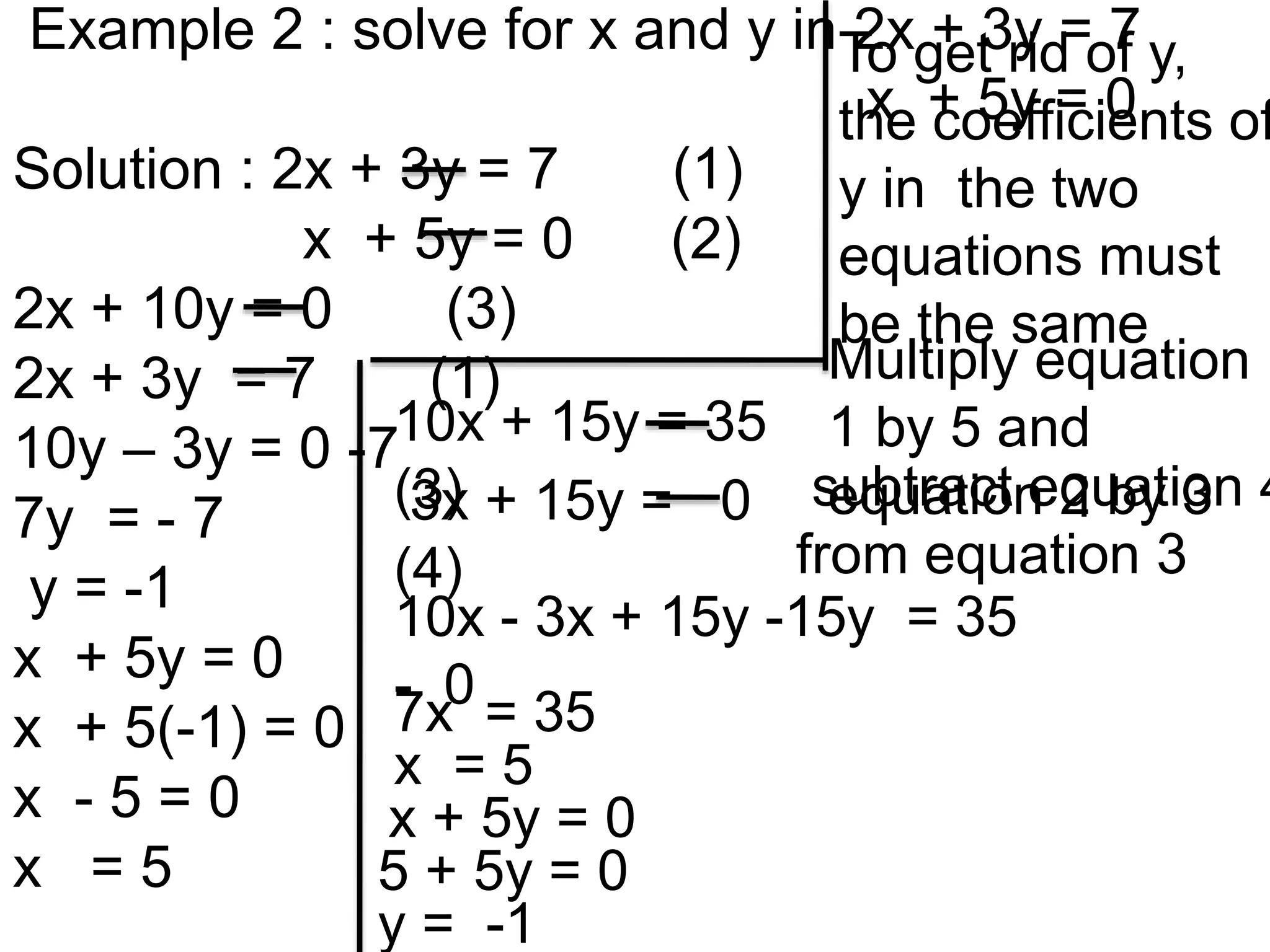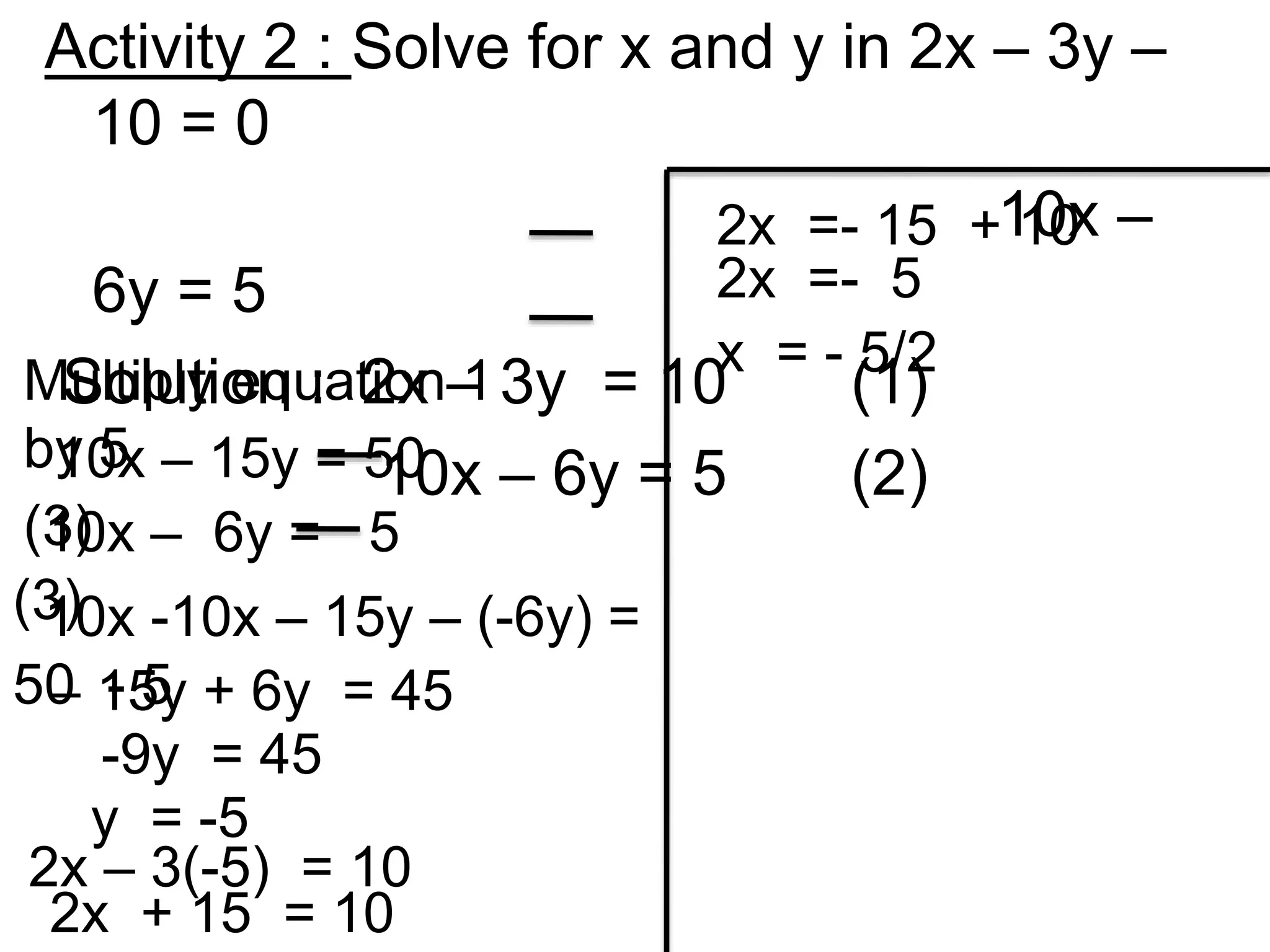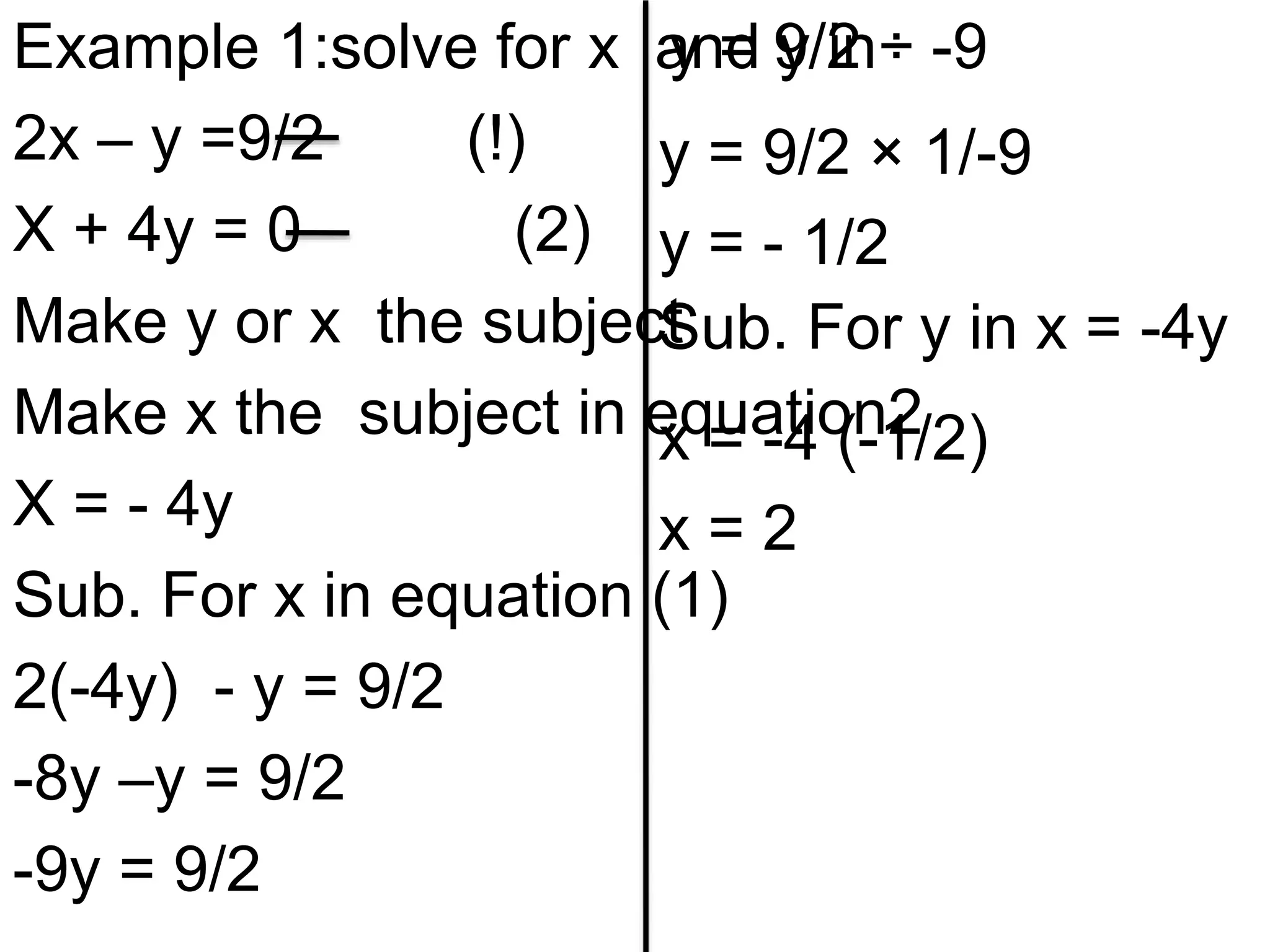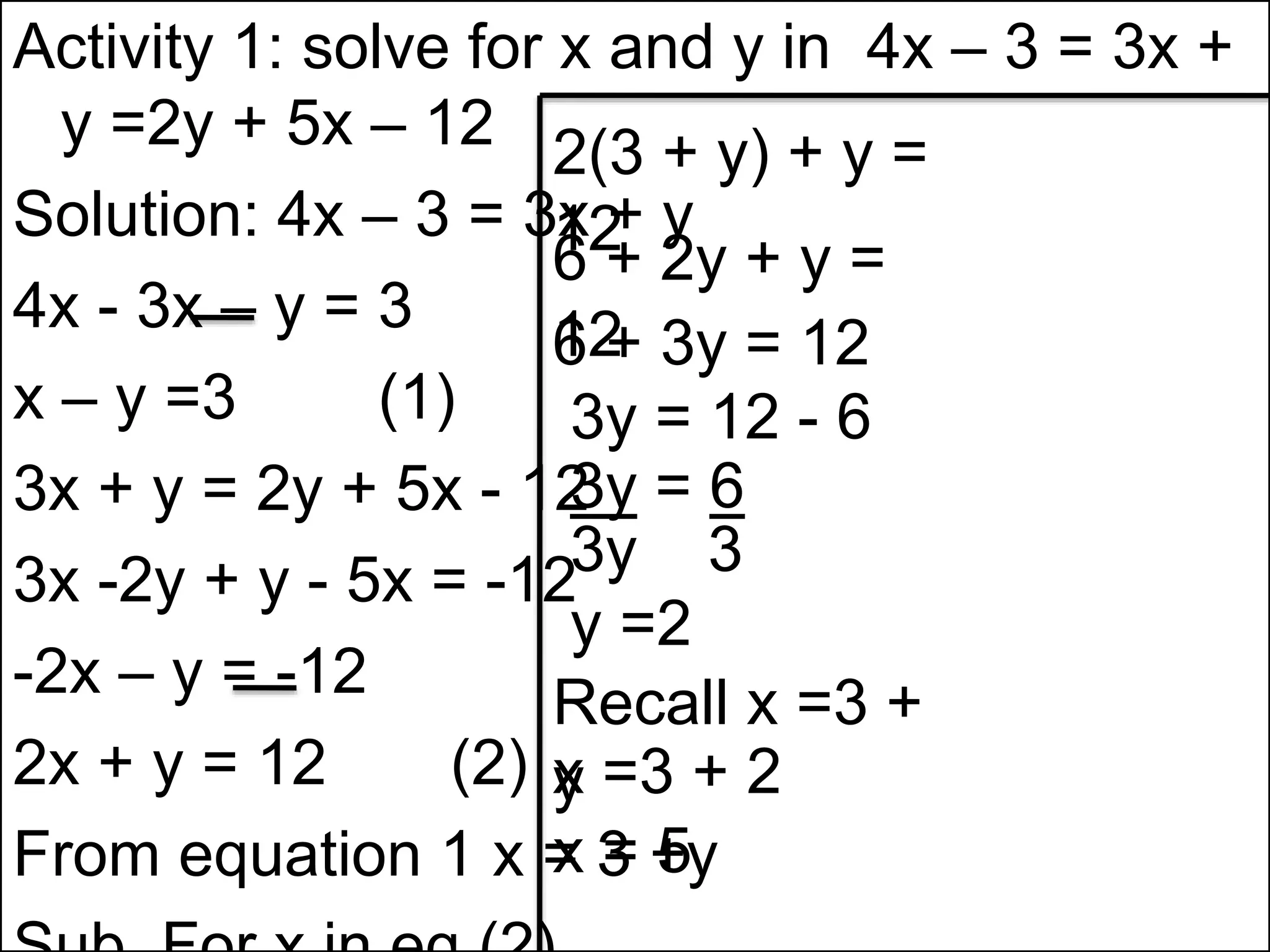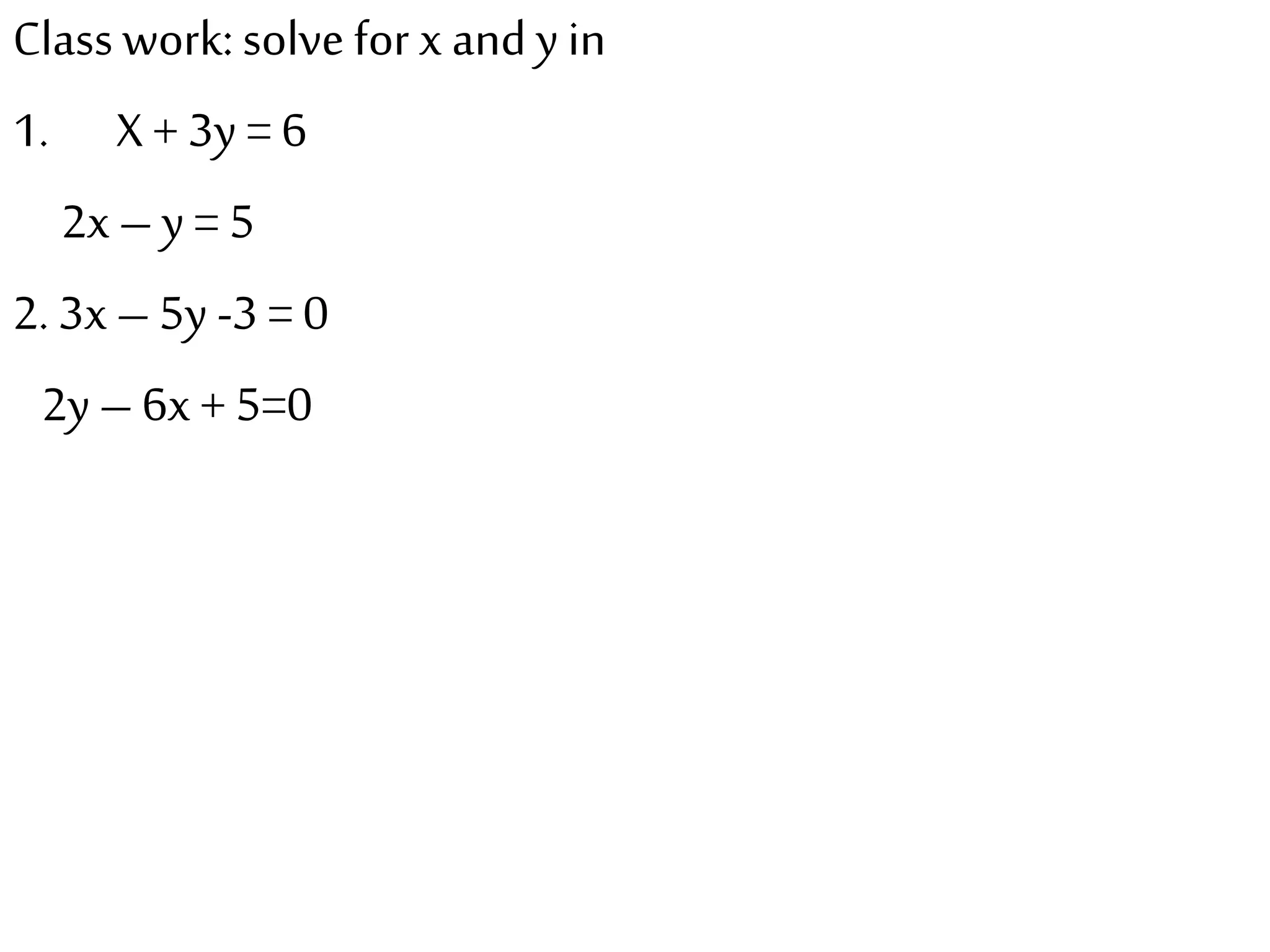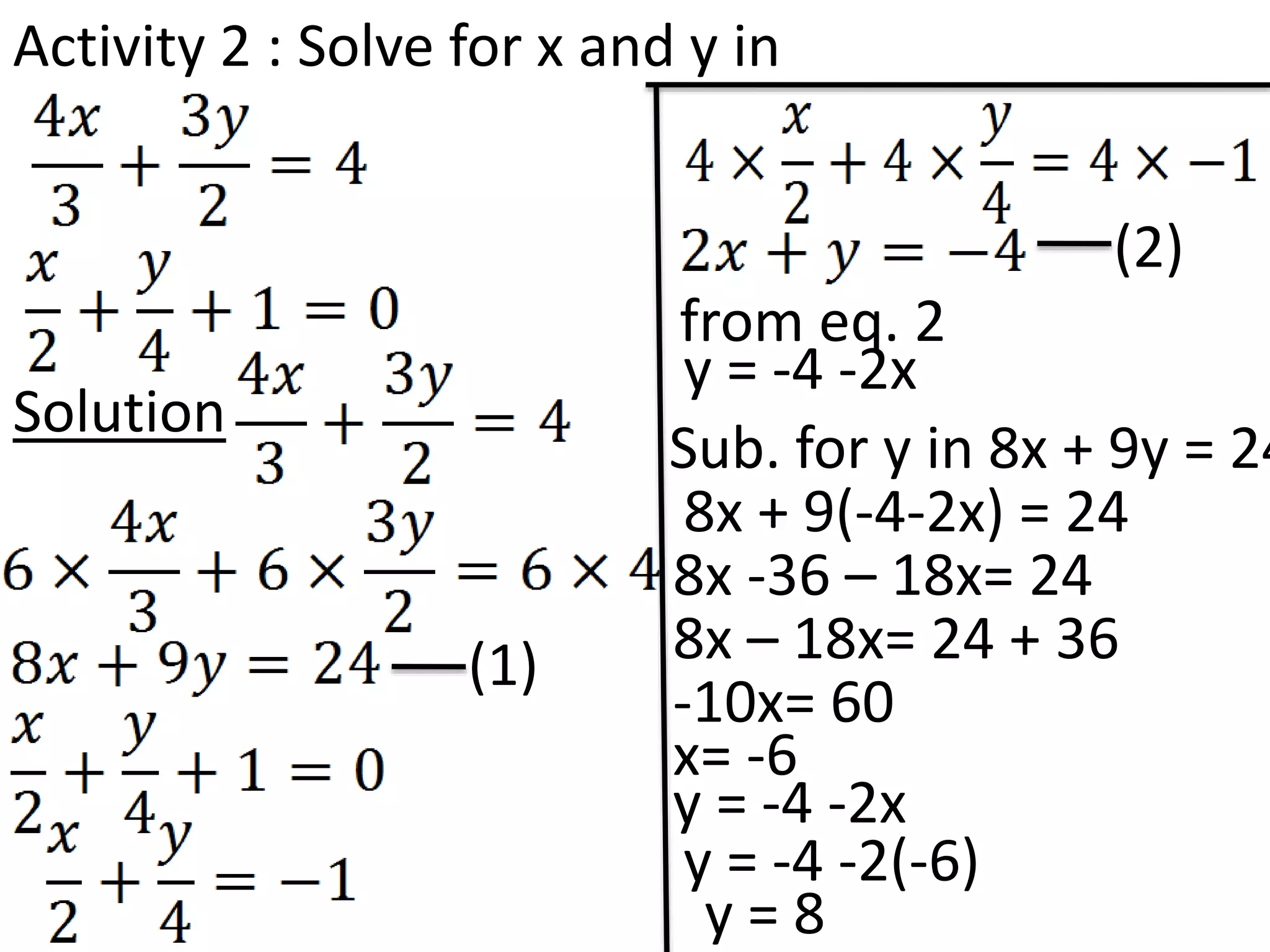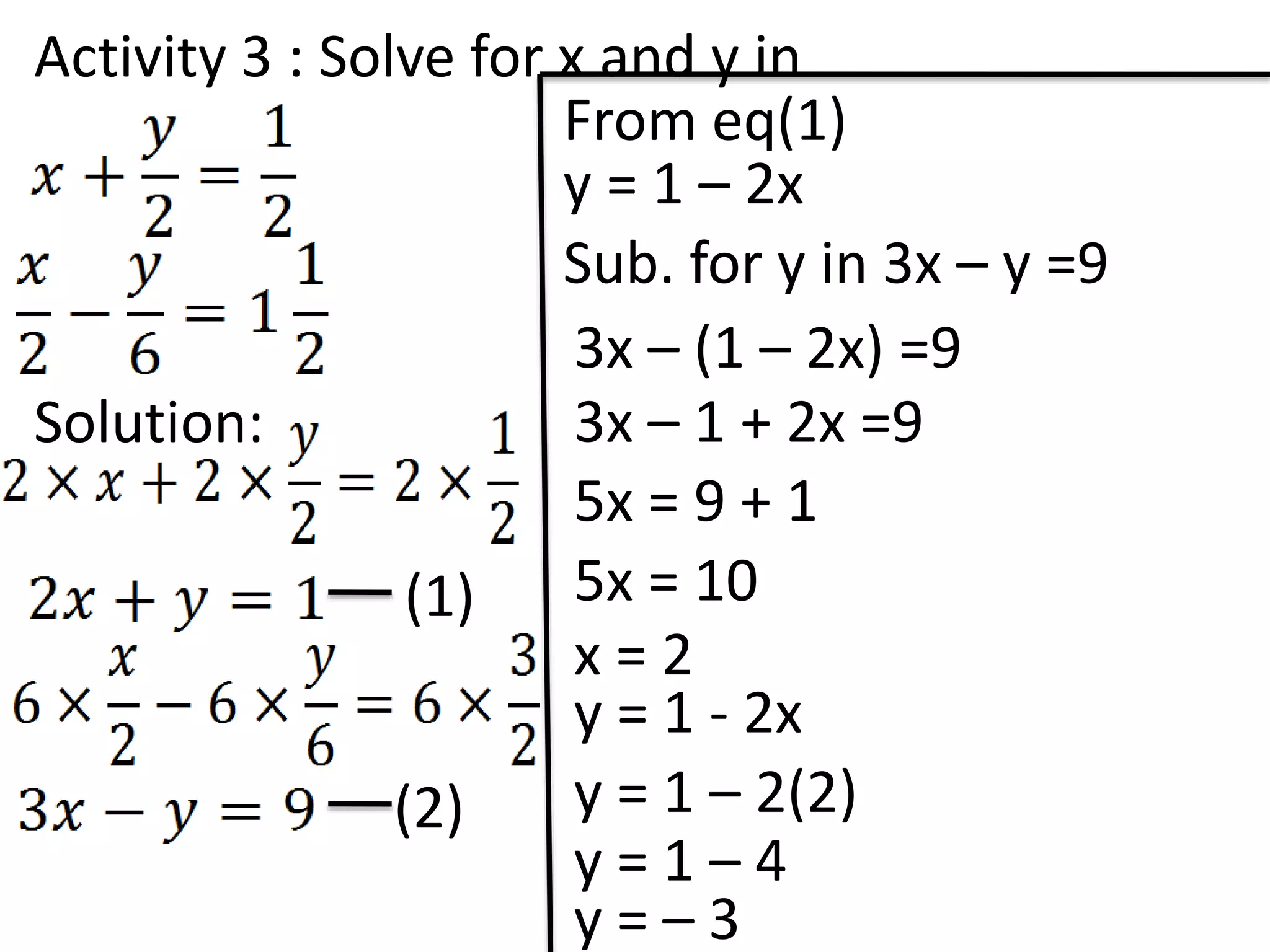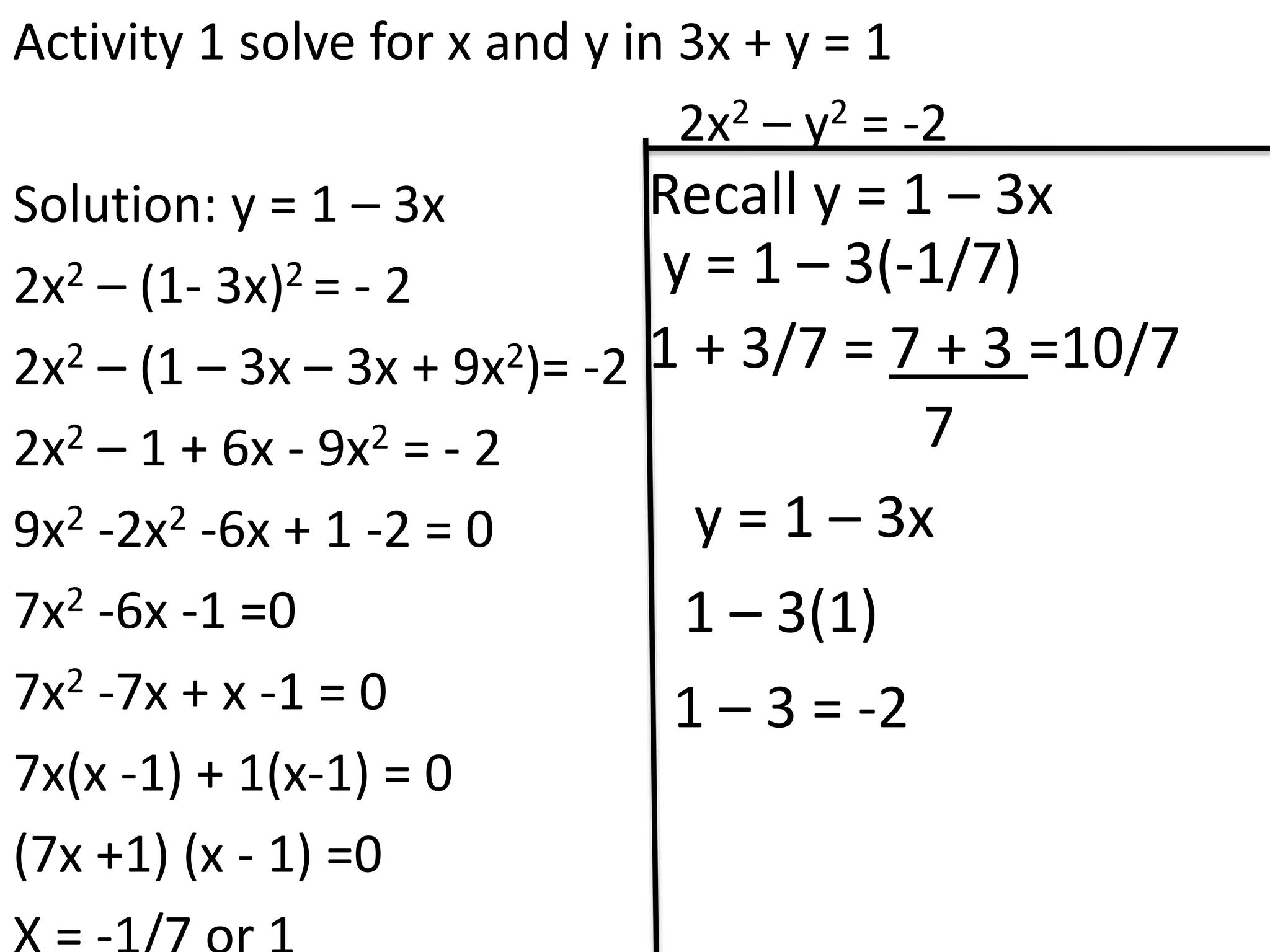The document discusses methods for solving simultaneous linear equations, including elimination and substitution. It provides examples of using elimination by adding or subtracting equations to remove a variable, and substitution by making one variable the subject of an equation and substituting it into the other equation. Fractions are converted to simple linear equations by finding a common denominator. The document also covers solving simultaneous equations when one equation is quadratic using substitution after making one variable the subject of the linear equation.

1. Simultaneous equations
Elimination and substitution
method

2. Objectives:
 solve simultaneous linear equations
by elimination method
 Solve simultaneous linear
equations by substitution method
Elimination method of solving
simultaneous equations
Elimination method:- this is to get rid off
one of the variables.

3. Conditions for elimination
The coefficient of the variables to get rid
off must be the same.
Addition operation is applied when the
variables are of different signs
Subtraction is used when the variables
are of the same signs.
Example 1: solve simultaneously x +2y =
7
x – y = 4
Solution: to eliminate means to get rid of

4. x +2y = 7 (1)
x – y = 4 (2)
x – x + 2y – (-Y) = 7- 4
2y + y = 3
3y = 3
y = 1
Substitute for y in any of the two equations
x – y = 4
x – 1 = 4
x = 4 + 1
x = 5
To get rid of x subtract equation
2 from equation 1

5. other way
x +2y = 7 (1)
x – y = 4 (2)
x +2y = 7 (1)
2x -2y = 8 (3)
3x = 15
x = 5
Substitute for x in any of the equation
x – y = 4
5 – y = 4
5 -4 = y
y = 1
To get rid of y, the coefficients of
y in the two equations must be
the sameMultiply equation 2 by 2
Add equation 1 to equation 3

6. Solve for x and y in x + y = 12
3x- y = 20
Solution: x + y = 12
3x- y = 20
x + 3x + y + (-y) = 12 +20
4x = 32
x = 8
x + y = 12
8 + y = 12
y = 12 – 8
y = 4
(1)
(2)
To get rid of x, the
coefficients of x in
the two equations
must be the sameMultiply equation 1
by 33x + 3y = 36(3)
3x - y = 20(2)
subtract equation 2 from
equation 33y –(-y) = 36 - 20
4y = 16
y = 4
substitute for y in any of the
equationsx + y = 12
x + 4 = 12
x = 12 - 8
x = 4

7. Example 2 : solve for x and y in 2x + 3y = 7
x + 5y = 0
Solution : 2x + 3y = 7 (1)
x + 5y = 0 (2)
2x + 10y = 0 (3)
2x + 3y = 7 (1)
10y – 3y = 0 -7
7y = - 7
y = -1
x + 5y = 0
x + 5(-1) = 0
x - 5 = 0
x = 5
To get rid of y,
the coefficients of
y in the two
equations must
be the same
Multiply equation
1 by 5 and
equation 2 by 3
10x + 15y = 35
(3)3x + 15y = 0
(4)
subtract equation 4
from equation 3
10x - 3x + 15y -15y = 35
- 07x = 35
x = 5
x + 5y = 0
5 + 5y = 0
y = -1

8. Activity 2 : Solve for x and y in 2x – 3y –
10 = 0
10x –
6y = 5
Solution : 2x – 3y = 10 (1)
10x – 6y = 5 (2)
Multiply equation 1
by 510x – 15y = 50
(3)10x – 6y = 5
(3)10x -10x – 15y – (-6y) =
50 - 5– 15y + 6y = 45
-9y = 45
y = -5
2x – 3(-5) = 10
2x + 15 = 10
2x =- 15 + 10
2x =- 5
x = - 5/2

9. Substitution method
Objectives : to make one of the variables
the subject in one of the equations
to substitute the new equation correctly into
the other equation
To solve for the unknown

10. Example 1:solve for x and y in
2x – y =9/2 (!)
X + 4y = 0 (2)
Make y or x the subject
Make x the subject in equation2
X = - 4y
Sub. For x in equation (1)
2(-4y) - y = 9/2
-8y –y = 9/2
-9y = 9/2
y = 9/2 ÷ -9
y = 9/2 × 1/-9
y = - 1/2
Sub. For y in x = -4y
x = -4 (-1/2)
x = 2

11. Activity 1: solve for x and y in 4x – 3 = 3x +
y =2y + 5x – 12
Solution: 4x – 3 = 3x + y
4x - 3x – y = 3
x – y =3 (1)
3x + y = 2y + 5x - 12
3x -2y + y - 5x = -12
-2x – y = -12
2x + y = 12 (2)
From equation 1 x = 3 +y
2(3 + y) + y =
126 + 2y + y =
126 + 3y = 12
3y = 12 - 6
3y = 6
3y 3
y =2
Recall x =3 +
yx =3 + 2
x = 5

12. Activity 2: solve for p and q in 3p -5q -4 =5p
+8 =2p + q + 7
Solution: 3p – 5q – 4 = 2p + q +7
3p – 2p – 5q –q = 7 + 4
P – 6q = 11 (1)
3p – 5q – 4 = 5p + 8
3p – 5p -5q = 8 + 4
-2p – 5q = 12 (2)
From eq. (1) p = 11 + 6q
Sub. For p in eq. (2)
-22 - 12q –
5q =12-12q – 5q =12 +
22-17q =-34
q = –2
Recall p =11
+ 6qp =11 + 6(-2)
p = 11 -12
p = -1

13. Class work: solve for x and yin
1. X + 3y = 6
2x – y = 5
2. 3x – 5y -3 = 0
2y – 6x + 5=0

14. Simultaneous equation with fractions
Objectives :
• To change the fractional equation to
simple linear equation
• To solve for the unknowns

15. Solve for x and y in
Solution : step 1
Find the lcm of the
denominators of each
of the equation
Step 2: multiply
each equation by
the
(1)
(2)
from eq. 1
x = 2 - y
Sub. For x in 2x + 3y =
-12(2-y) + 3y = -1
4 – 2y + 3y = -1
4 + y = -1
y = -1 - 4
y = -5

16. Recall x = 2 – y
x = 2 – (-5)
x = 2 + 5
x = 7
Activity 1: Solve for x and y in
Solution
(1)
(2)
Multiply eq (1) by2
10x – 8y = 4 (3)
10x – 9y = 2 (2)
10x-10x -8y –(-9y ) =
2-8y + 9y = 2
y = 2
10x – 9(2) = 2
10x – 18 = 2
10x = 20

17. Activity 2 : Solve for x and y in
Solution
(1)
(2)
from eq. 2
y = -4 -2x
Sub. for y in 8x + 9y = 24
8x + 9(-4-2x) = 24
8x -36 – 18x= 24
8x – 18x= 24 + 36
-10x= 60
x= -6
y = -4 -2x
y = -4 -2(-6)
y = 8

18. Activity 3 : Solve for x and y in
Solution:
(1)
(2)
From eq(1)
y = 1 – 2x
Sub. for y in 3x – y =9
3x – (1 – 2x) =9
3x – 1 + 2x =9
5x = 9 + 1
5x = 10
x = 2
y = 1 - 2x
y = 1 – 2(2)
y = 1 – 4
y = – 3

19. Solve the following equations simultaneously

20. Simultaneous equation with quadratic
equation
Objectives: to make the variable the
subject
To be able to substitute correctly
To be able to solve for the unknown from
quadratic equations

21. Example 1: solve for x and y in
X + 3y= 2 (1)
x2 + 2y =3 (2)
Solution: make x the
Subject in eq.(1)
x = 2 - 3y
Sub. for x in eq.(2)
(2- 3y)2 + 2y = 3
4 – 6y – 6y + 9y2 + 2y = 3
4 – 12y + 2y +9y2 - 3 = 0
9y2 -10y + 1 = 0
9y2 – 9y – y + 1= 0
9y(y – 1) –1(y – 1)= 0
(9y –1)(y – 1)= 0
y = 1/9 or 1
Sub. For y in x = 2- 3y
x =2 – 3(1)
x =2 – 3
x = –1
x =2 – 3(1/9)
x =2 –1/3
x = 5/3

22. Activity 1 solve for x and y in 3x + y = 1
2x2 – y2 = -2
Solution: y = 1 – 3x
2x2 – (1- 3x)2 = - 2
2x2 – (1 – 3x – 3x + 9x2)= -2
2x2 – 1 + 6x - 9x2 = - 2
9x2 -2x2 -6x + 1 -2 = 0
7x2 -6x -1 =0
7x2 -7x + x -1 = 0
7x(x -1) + 1(x-1) = 0
(7x +1) (x - 1) =0
Recall y = 1 – 3x
y = 1 – 3(-1/7)
1 + 3/7 = 7 + 3 =10/7
7
y = 1 – 3x
1 – 3(1)
1 – 3 = -2

23. Activity2: Solve for x and y in 2x + y = 4 and
x2 + xy = -12
Solution: 2x + y = 4
y = 4 – 2x
Sub. for y in x2 + xy = -12
x2 + x(4 - 2x) = -12
x2 + 4x -2x2 =-12
-x2 + 4x =-12
-x2 + 4x + 12 = 0
-x2 – 2x + 6x + 12 = 0
-x (x + 2) + 6(x +2) = 0
(6 - x)(x + 2) = 0
x = -2 or 6
y = 4 – 2x
y = 4 – 2(-2)
y = 4 + 4 = 8
y = 4 – 2(6)
y = 4 – 12
y = -8

24. Activity3: Solve for x and y in x + y = 14 and
2xy + 1 = 21
Solution: x =14 – y
Sub. for x in 2xy + 1 = 21
2y(14 - y) + 1 = 21
28y -2y2 + 1 = 21
2y2 – 28y + 20 = 0
y2 - 14y + 10 = 0