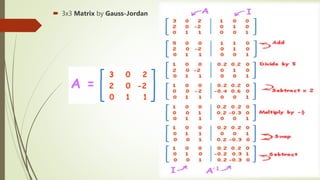
The document discusses matrix inversion. A matrix inverse undoes multiplication by a matrix, just as a number's reciprocal undoes multiplication. To find a matrix inverse, Crammer's method or Gauss-Jordan elimination can be used. The inverse allows solving equations involving matrix multiplication, such as finding X when XA=B, by multiplying both sides by the inverse A-1. MATLAB has commands like inv() and ^(-1) to compute inverses of square matrices.

1. Matrix Inversion

2. What is the Inverse of a Matrix?
 This is the Reciprocal of a Number:
 The Inverse of a Matrix is the same idea but we write it A-1

3.  When we multiply a number by its reciprocal we get 1
8 × (1/8) = 1
 When we multiply a Matrix by its Inverse we get the Identity Matrix
(which is like "1" for Matrices):
A × A-1 = I
 Why not 1/A ?
 And anyway 1/8 can also be written 8-1
 Identity Matrix
 The Identity Matrix is the matrix equivalent of the number "1"

4. Why Do We Need an Inverse?
 Because with Matrices we don't divide! Seriously, there is no concept of dividing
by a Matrix.
 But we can multiply by an Inverse, which achieves the same thing.
 EX : Say we want to find Matrix X, and we know Matrix A and B:
XA = B
X=B/A Isn’t valid as we can't divide.
But we can multiply both sides by A-1
XAA-1 = BA-1
X I = BA-1
X = BA-1

5. how do we calculate the Inverse?
 There are usually two methods to find the inverse of a matrix. These are:
 1..Crammer’s Method
 2..Gauss-Jordan elimination Method
(This is called the "Augmented Matrix“)

6. Examples:
 2x2 Matrix by Crammer’s Method

7.  3x3 Matrix by Gauss-Jordan

8. Matrix Inversion In MATLAB
 The inv( x ) , x^(-1) commands compute the inverse of a square matrix:

9. References
 https://en.wikipedia.org/wiki/Invertible_matrix
 https://www.mathsisfun.com/algebra/matrix-inverse.html
 https://www.slideshare.net/itutor/inverse-matrix-determinants
 https://en.wikipedia.org/wiki/Invertible_matrix
By Abdalla Saad