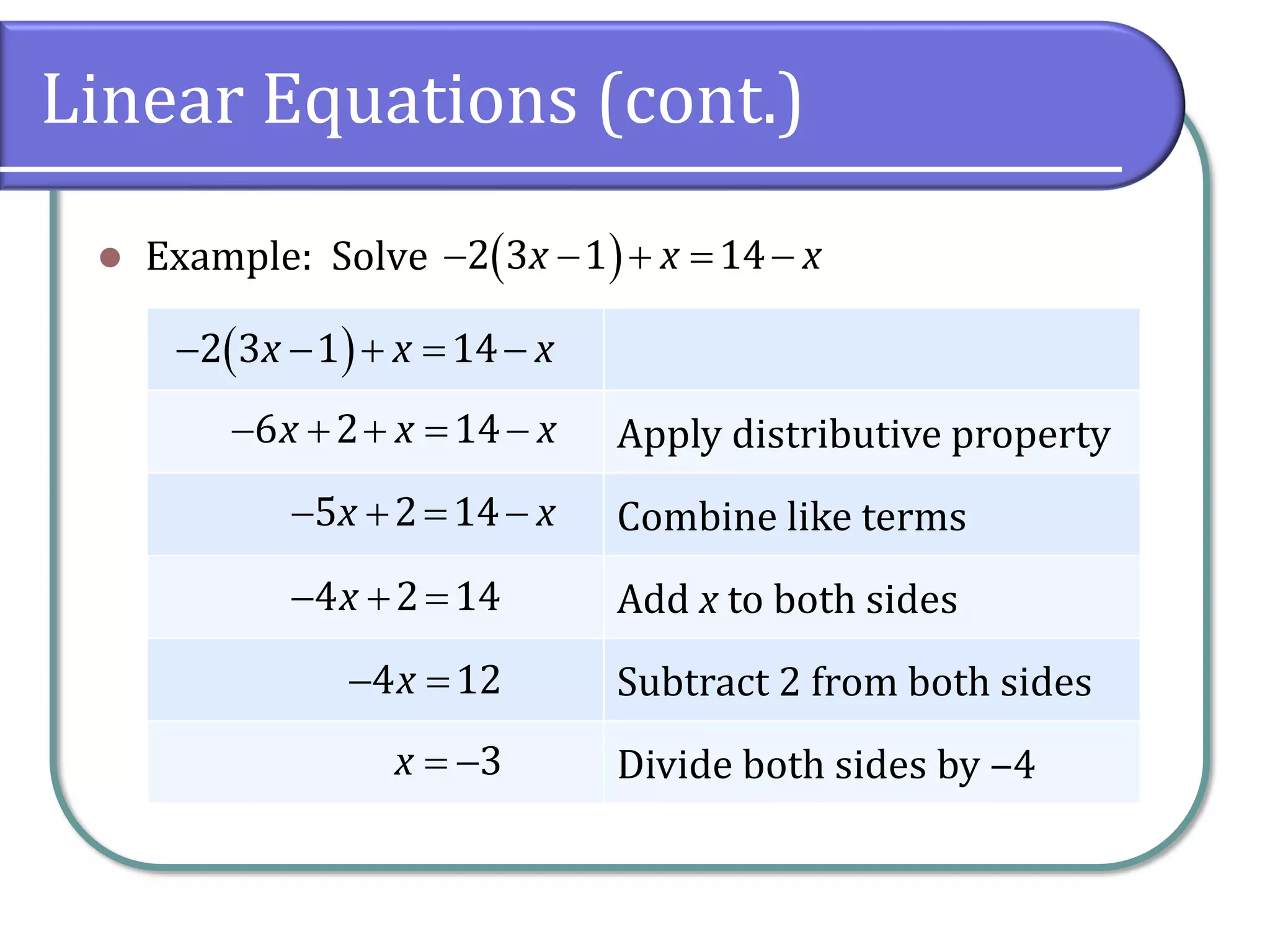
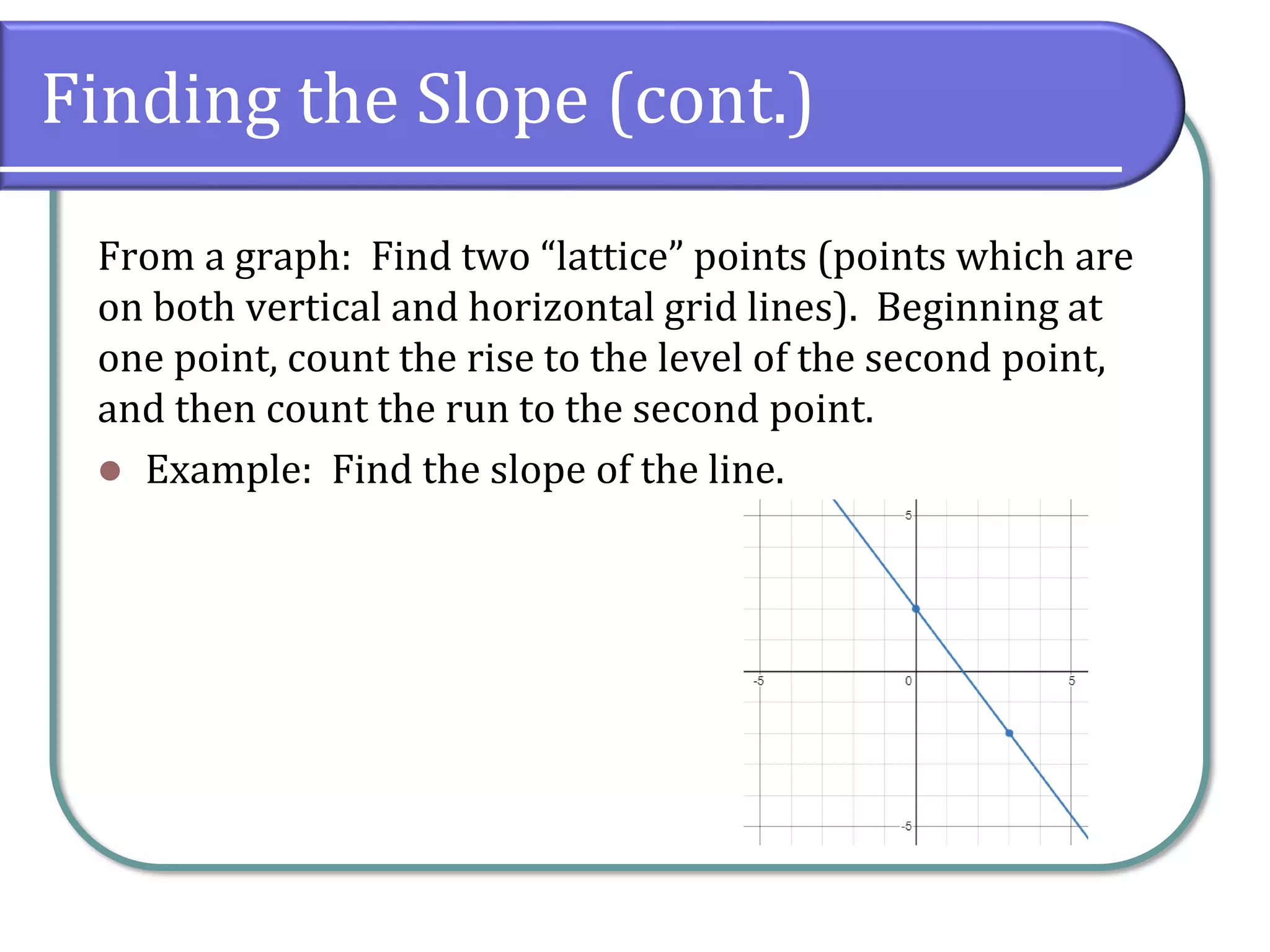
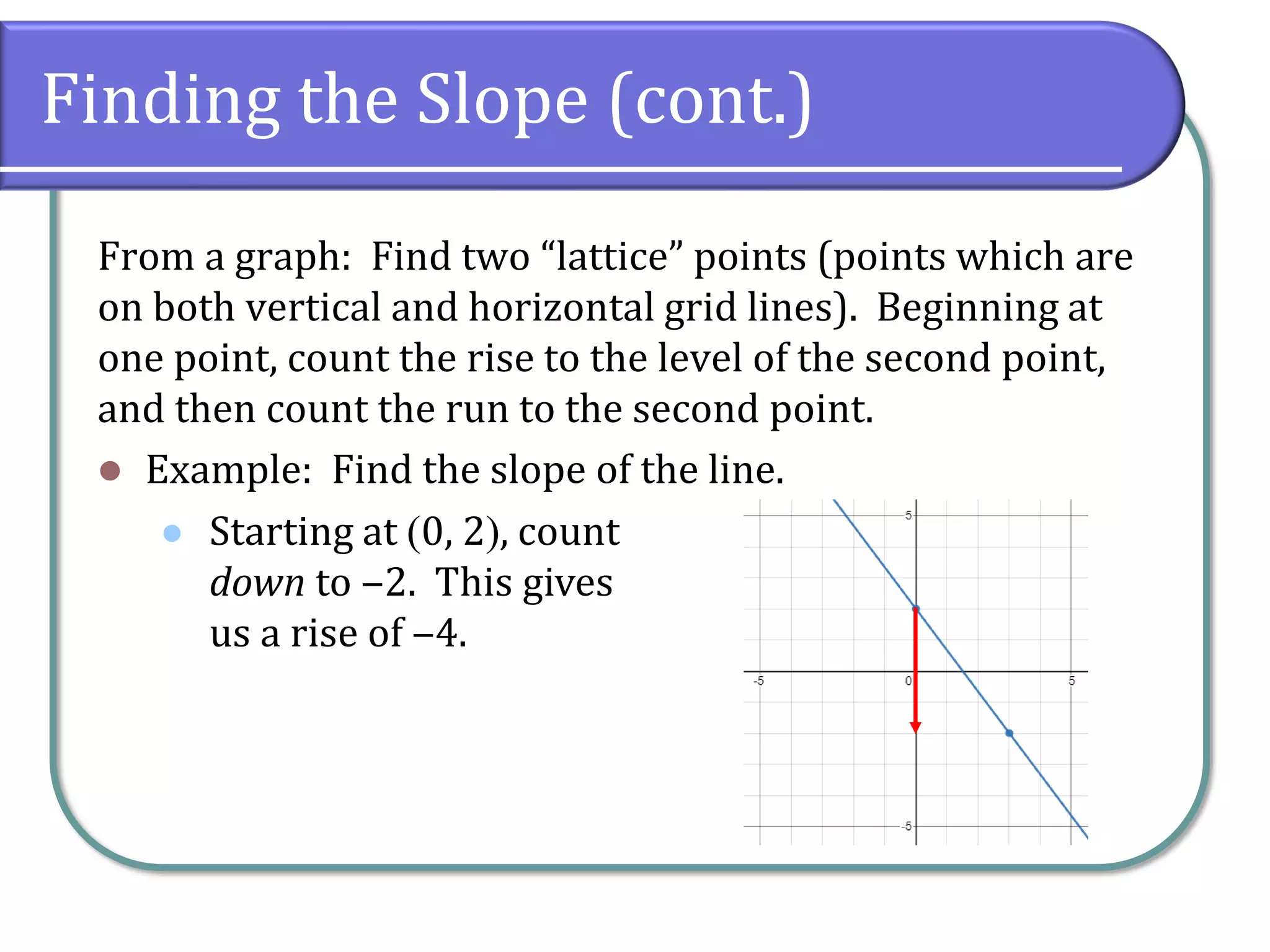
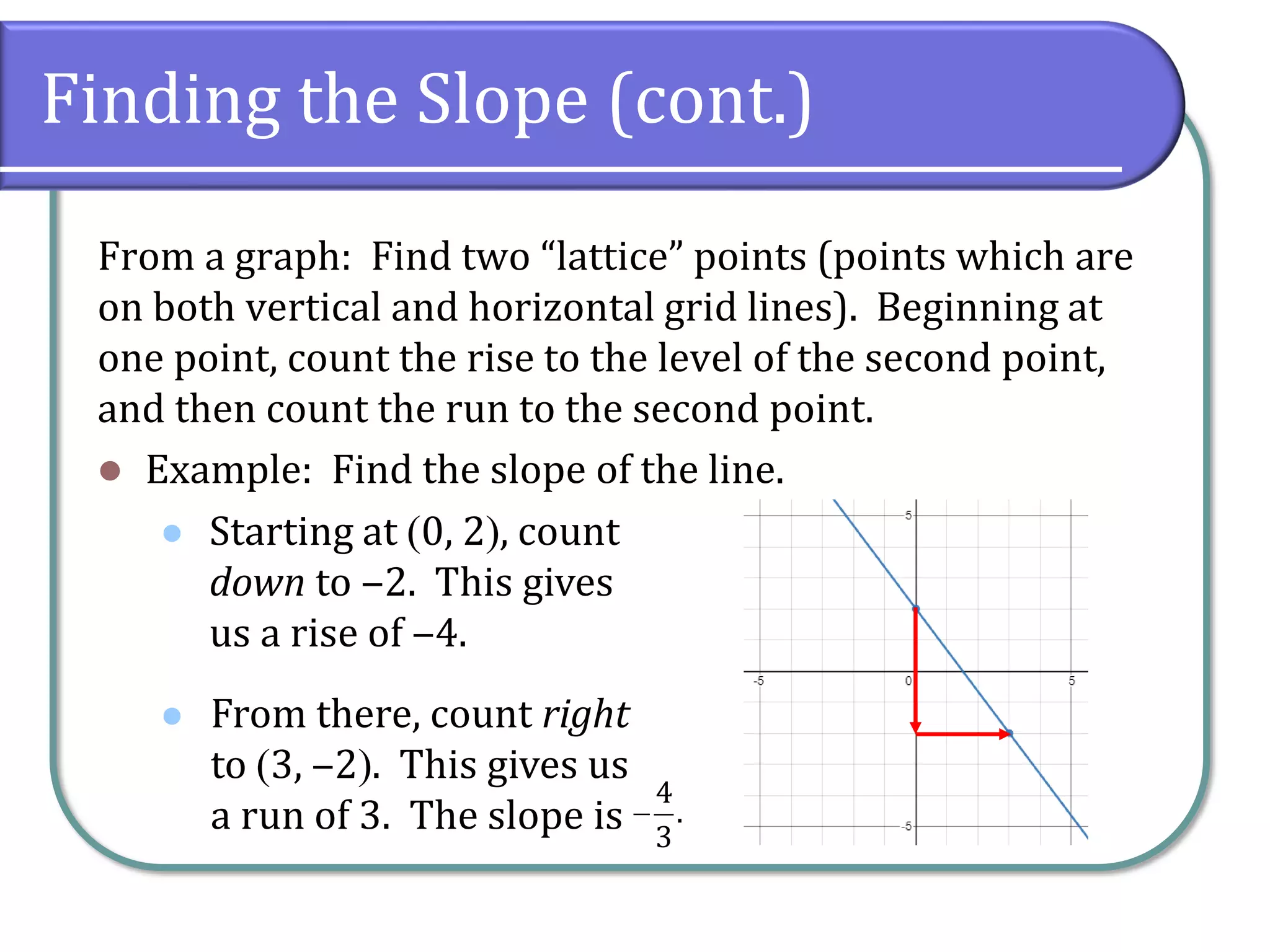
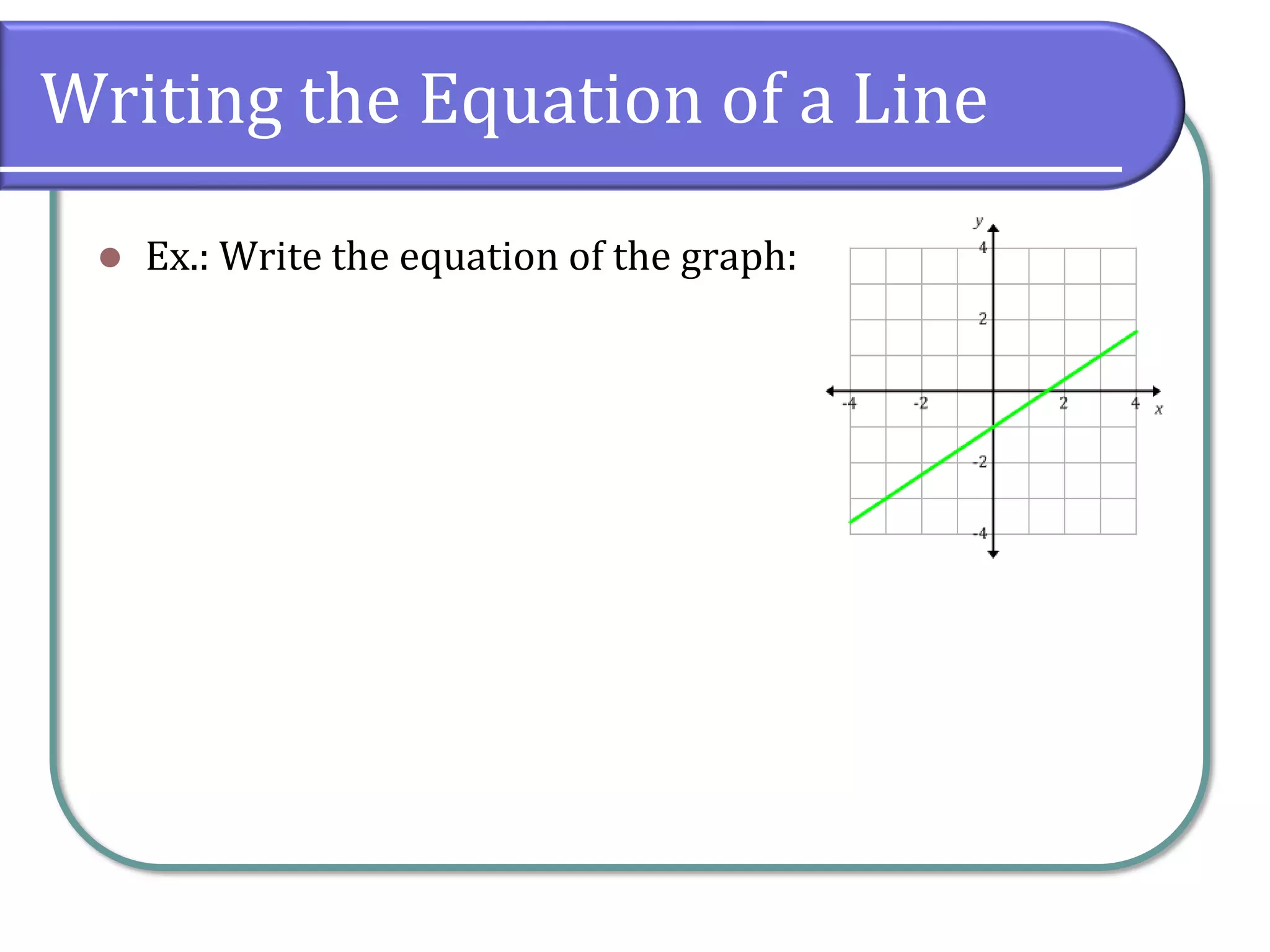
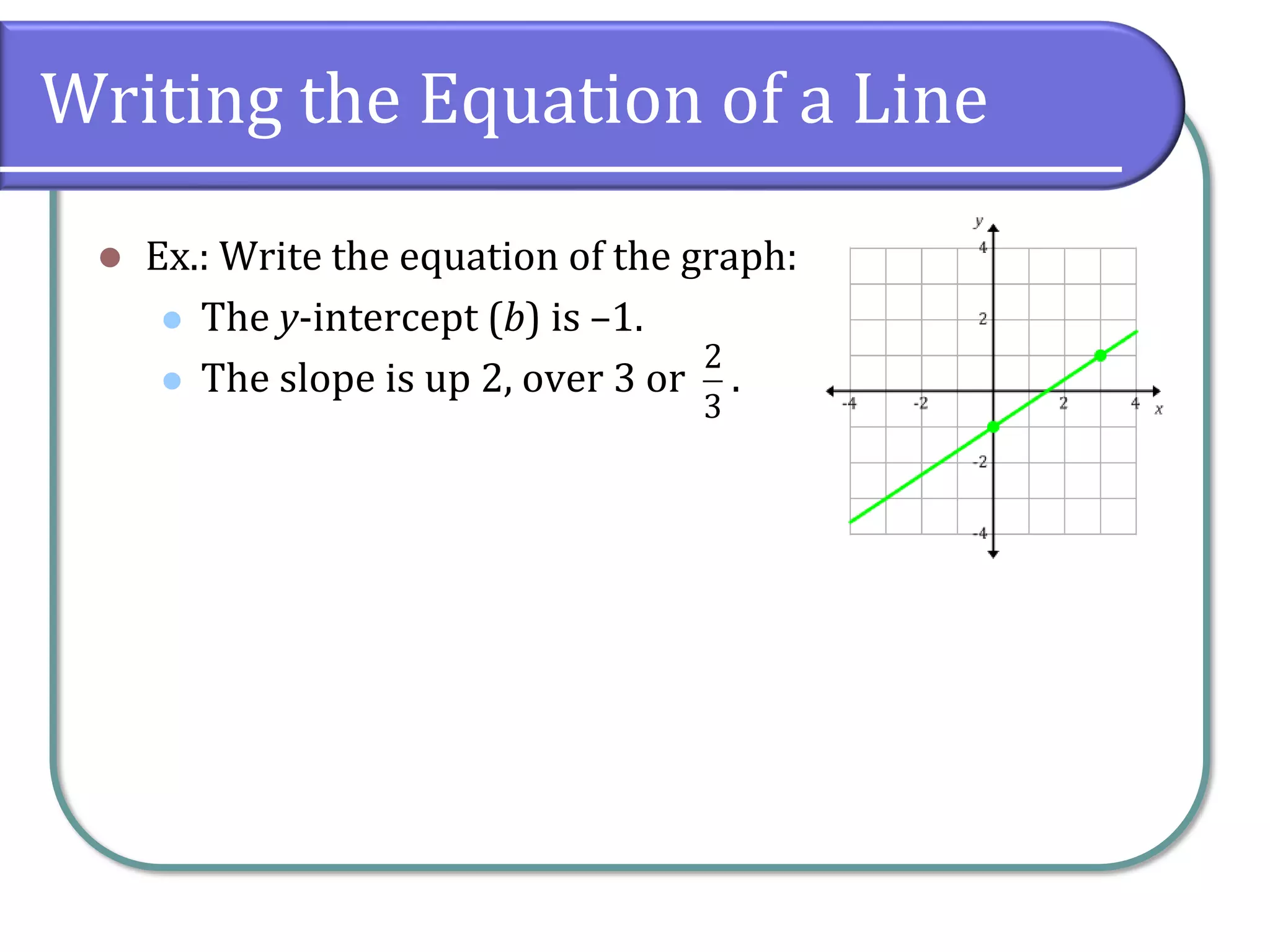
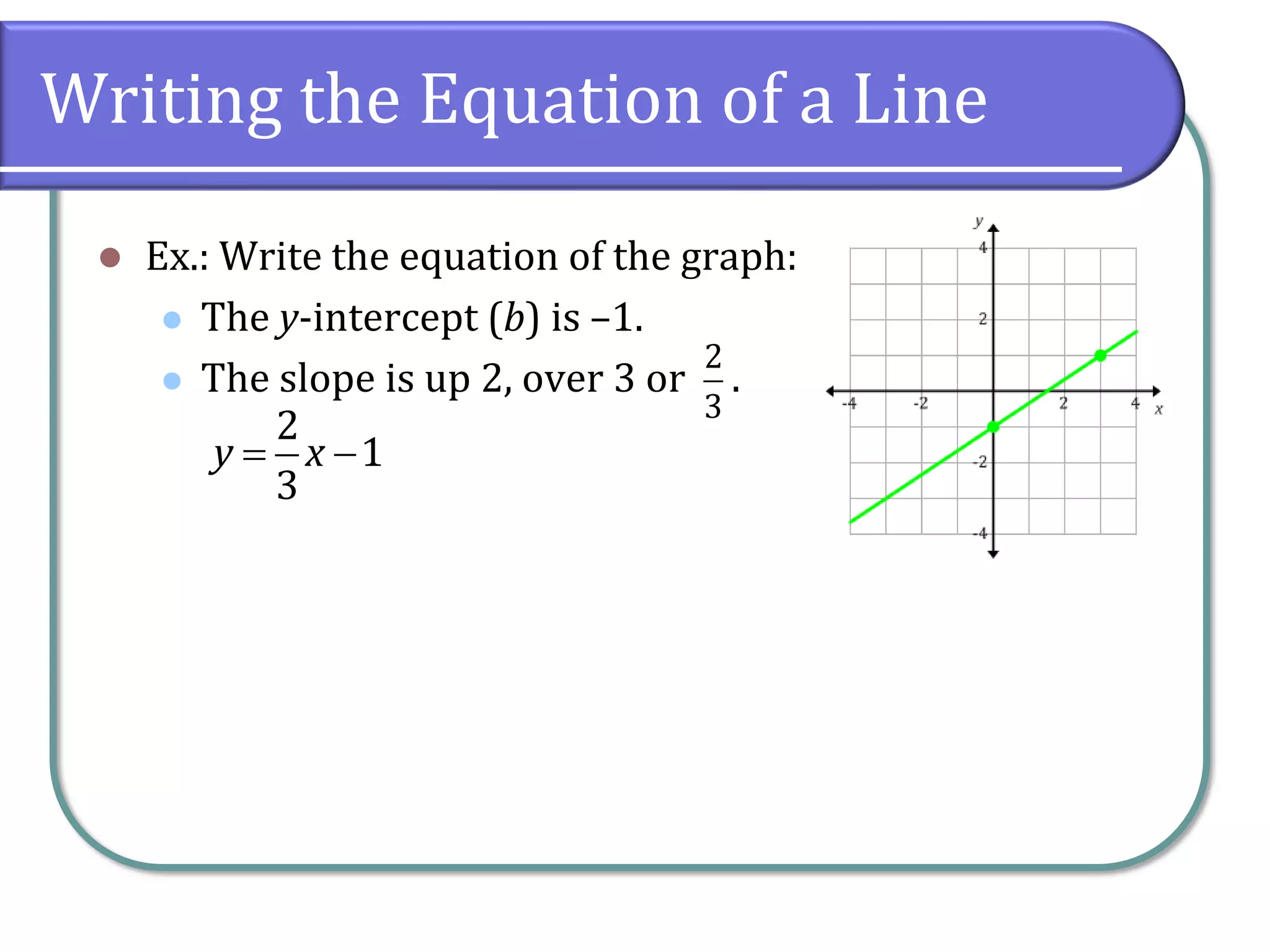
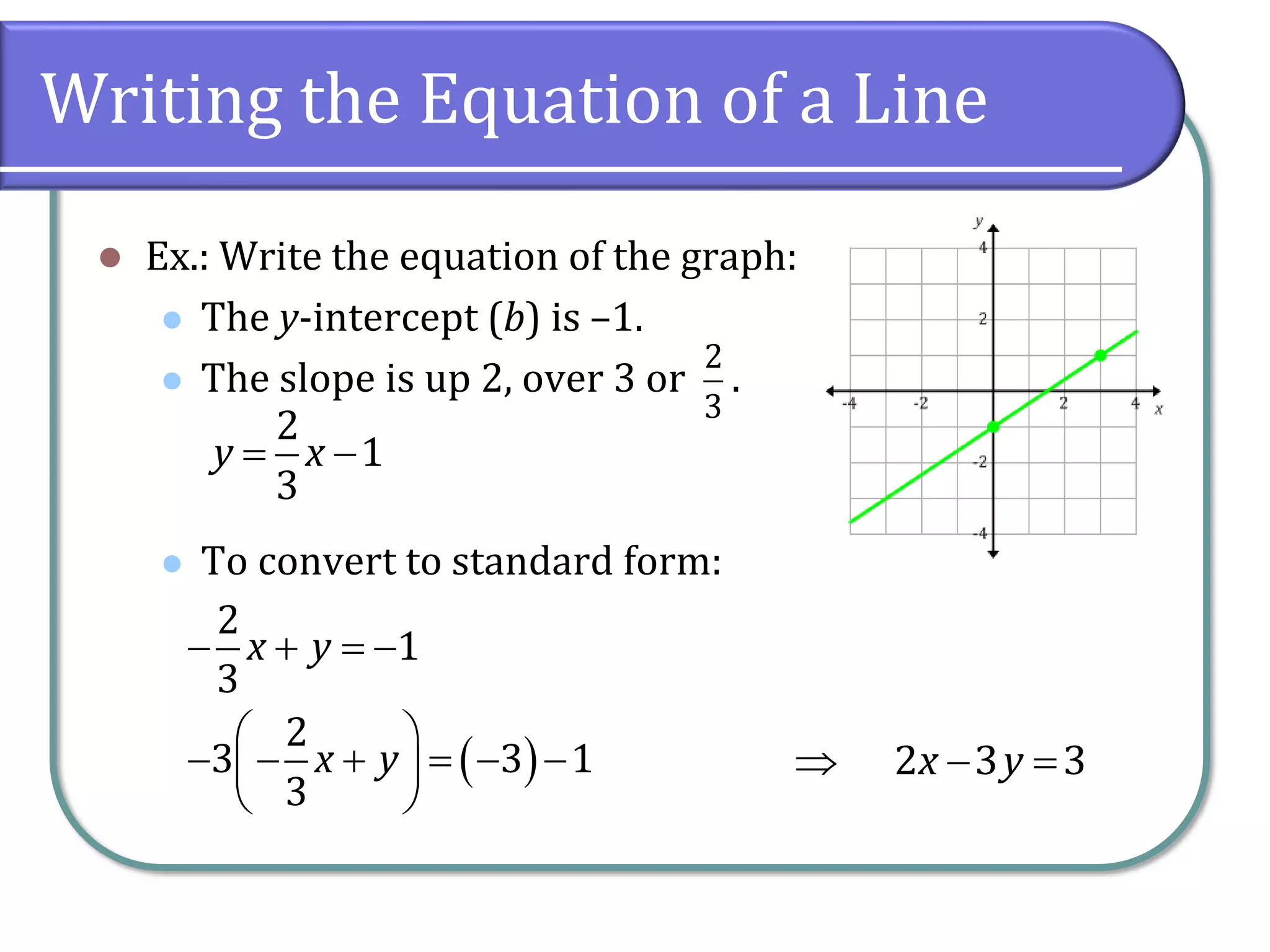
This document provides an overview of linear equations, including how to solve them, classify their solutions, and determine the slope and equations of lines. It covers key concepts such as the addition and multiplication properties of equality, rational equations, and the characteristics of parallel and perpendicular lines. Additionally, it includes example problems and classwork assignments for practice.

1. 2.2 Linear Equations
Chapter 2 Equations and Inequalities

2. Concepts and Objectives
⚫ Objectives for this section:
⚫ Solve equations in one variable algebraically.
⚫ Solve a rational equation.
⚫ Find a linear equation.
⚫ Given the equations of two lines, determine whether
their graphs are parallel or perpendicular.
⚫ Write the equation of a line parallel or perpendicular
to a given line.

3. Basic Properties of Equations
⚫ An equation is a statement that two expressions are
equal. (Ex.: x + 2 = 9 or 7y +1 = 5y + 23)
⚫ To solve an equation means to find all numbers that
make the equation a true statement. These numbers are
called solutions or roots of the equation. The set of all
solutions to an equation is called its solution set.
⚫ We can use the addition and multiplication
properties of equality to help us solve equations.

4. Basic Properties of Equations
⚫ Addition (and Subtraction) Property of Equality:
⚫ Multiplication (and Division) Property of Equality:
For real numbers a, b, and c:
If a = b, then ac = bc
If a = b and c  0, then
a b
c c
=
For real numbers a, b, and c:
If a = b, then a + c = b + c
If a = b, then a ‒ c = b ‒c

5. Linear Equations
⚫ A linear equation in one variable is an equation that
can be written in the form
ax + b = 0,
where a and b are real numbers and a  0.
⚫ A linear equation is also called a first-degree equation
since the degree of the variable is either one or zero.
⚫ To solve a linear equation, use the properties of equality
to isolate the variable on one side and the solution on
the other.

6. Linear Equations (cont.)
⚫ Example: Solve ( )
2 3 1 14
x x x
− − + = −
Apply distributive property
Combine like terms
Add x to both sides
Subtract 2 from both sides
Divide both sides by ‒4
( )
2 3 1 14
x x x
− − + = −
6 2 14
x x x
− + + = −
5 2 14
x x
− + = −
4 2 14
x
− + =
4 12
x
− =
3
x = −

7. Linear Equations (cont.)
⚫ If solving a linear equation leads to
⚫ a true statement such as 0 = 0, the equation is an
identity. Its solution set is  or {all real numbers}.
⚫ a single solution such as x = 3, the equation is
conditional. Its solution set consists of a single
element.
⚫ a false statement such as 0 = 7, the equation is a
contradiction. Its solution set is  or { }.

8. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6
⚫ 5x ‒ 4 = 11
⚫ 2x +5 + x = 3x + 9

9. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6
3x + 6 ‒ x = 2x + 6
2x + 6 = 2x + 6
0 = 0
⚫ 5x ‒ 4 = 11
⚫ 2x +5 + x = 3x + 9

10. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6 identity 
3x + 6 ‒ x = 2x + 6
2x + 6 = 2x + 6
0 = 0
⚫ 5x ‒ 4 = 11
⚫ 2x +5 + x = 3x + 9

11. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6 identity 
⚫ 5x ‒ 4 = 11
5x = 15
x = 3
⚫ 2x +5 + x = 3x + 9

12. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6 identity 
⚫ 5x ‒ 4 = 11 conditional {3}
5x = 15
x = 3
⚫ 2x +5 + x = 3x + 9

13. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6 identity 
⚫ 5x ‒ 4 = 11 conditional {3}
⚫ 2x +5 + x = 3x + 9
3x + 5 = 3x + 9
0 = 4

14. Linear Equations (cont.)
Example: Decide whether each equation is an identity,
conditional equation, or a contradiction. Give the solution
set.
⚫ 3x + 2 ‒ x = 2x + 6 identity 
⚫ 5x ‒ 4 = 11 conditional {3}
⚫ 2x +5 + x = 3x + 9 contradiction 
3x + 5 = 3x + 9
0 = 4

15. Rational Equations
⚫ A rational equation is an equation that has a rational
expression for one or more terms.
⚫ To solve a rational equation, multiply both sides by the
lowest common denominator of the terms of the
equation. Be sure to check your solution against the
undefined values!
Because a rational expression is not defined when its
denominator is 0, any value of the variable which makes
the denominator’s value 0 cannot be a solution.

16. Rational Equations (cont.)
⚫ Example: Solve
The lowest common denominator is , which is
equal to 0 if x = ‒1. Write this as .
−
+ =
+
2 3 5
2 1
x x
x
x
( )
+
2 1
x
 −1
x
( ) ( ) ( )( )
+ +
−
   
+ =
   
+
 
+
 
2 1 2 1
2 3
2
5
1
2 1
x x
x
x x x x
( )( ) ( ) ( )( )
+ − + = +
1 2 3 2 5 2 1
x x x x x
− − + = +
2 2
2 3 10 2 2
x x x x x
=
7 3
x
=
3
7
x
Since this is not ‒1, this is a
valid solution.
 
 
 
3
7

17. Rational Equations (cont.)
⚫ Example: Solve
The LCD is which is equal to . If x is
either 3 or ‒3, the denominator will be 0, so .
The only value of x which will satisfy the equation is 3,
but that is a restricted value, so the solution is .
− −
+ =
− + −
2
2 3 12
3 3 9
x x x
( )( )
+ −
3 3
x x −
2
9
x
 3
x
( ) ( )
− + + − = −
2 3 3 3 12
x x
− − + − = −
2 6 3 9 12
x x
− = −
15 12
x
=3
x


18. Rational Equations (cont.)
⚫ Example: Solve
The LCD is xx ‒ 2, which means x  0, 2.
2
3 2 1 2
2 2
x
x x x x
+ −
+ =
− −
 
1
−
( ) ( ) ( )
( )
 
+ −
   
+ =  
     
− −
   
− − −
 
3 2 1 2
2
2 2 2
2
x x
x
x
x x
x x
x x
x
( ) ( )
+ + − = −
3 2 2 2
x x x
= −
0, 1
x
+ + − = −
2
3 2 2 2
x x x
+ =
2
3 3 0
x x
( )
+ =
3 1 0
x x

19. Slope
⚫ The slope of a linear function is defined as the rate of
change or the ratio of rise to run.
⚫ If the slope is positive, the line slants to the right; if the
slope is negative, the line slants to the left.
⚫ We can use the slope formula to calculate the slope
between two points on a line.
The slope m of the line through the
points and is
( )
1 1
,
x y ( )
2 2
,
x y
2 1
2 1
rise
run
y y
m
x x
−
= =
−

20. Equations of Lines
⚫ An equation of a line can be written in one of the
following forms:
⚫ Standard form: Ax + By = C, where A, B, C  , A 0,
and A, B, and C are relatively prime
⚫ Point-slope form: y – y1 = m(x – x1), where m   and
(x1, y1) is a point on the graph
⚫ Slope-intercept form: y = mx + b, where m, b  
⚫ You should recall that in slope-intercept form, m is the
slope and b is the y-intercept (where the graph crosses
the y-axis).
⚫ If A = 0, then the graph is a horizontal line at y = b.

21. Equations of Lines (cont.)
⚫ If the x-values are the same between two points, the
slope formula produces a 0 in the denominator. Since
we cannot divide by 0, we say that a line of the form x = a
has no slope, and is a vertical line.
⚫ Technically, a vertical line is not a function at all,
because one value of x has more than one y value
(actually an infinite number of y values), but since it is a
straight line, we include it along with the linear
functions.

22. Finding the Slope
Using the slope formula:
⚫ Example: Find the slope of the line through the points
(–4, 8), (2, –3).
( )
3 8
2 4
m
− −
=
− −
x1 y1 x2 y2
–4 8 2 –3
11
6
−
=
11
6
= −

23. Finding the Slope (cont.)
From an equation: Convert the equation into slope-
intercept form (y = mx + b) if necessary. The slope is the
coefficient of x.
⚫ Example: What is the slope of the line y = –4x + 3?
The equation is already in slope intercept form, so the
slope is the coefficient of x, so m = –4.

24. Finding the Slope (cont.)
From a graph: Find two “lattice” points (points which are
on both vertical and horizontal grid lines). Beginning at
one point, count the rise to the level of the second point,
and then count the run to the second point.
⚫ Example: Find the slope of the line.

25. Finding the Slope (cont.)
From a graph: Find two “lattice” points (points which are
on both vertical and horizontal grid lines). Beginning at
one point, count the rise to the level of the second point,
and then count the run to the second point.
⚫ Example: Find the slope of the line.
⚫ Starting at (0, 2), count
down to ‒2. This gives
us a rise of ‒4.

26. Finding the Slope (cont.)
From a graph: Find two “lattice” points (points which are
on both vertical and horizontal grid lines). Beginning at
one point, count the rise to the level of the second point,
and then count the run to the second point.
⚫ Example: Find the slope of the line.
⚫
⚫
Starting at (0, 2), count
down to ‒2. This gives
us a rise of ‒4.
From there, count right
to (3, ‒2). This gives us
a run of 3. The slope is
4
.
3
−

27. Finding the Slope (cont.)
⚫ Example: What is the slope of the line 3x + 4y = 12?
The slope is .
3 4 12
4 3 12
x y
y x
+ =
= − +
3
3
4
y x
= − +
3
4
−

28. Parallel and Perpendicular Lines
⚫ Nonvertical lines are parallel iff (if and only if) they have
the same slope. Any two vertical lines are parallel.
⚫ Two nonvertical lines are perpendicular iff the product
of their slopes is –1 (negative reciprocals). Vertical and
horizontal lines are perpendicular.
⚫ Example: What is the slope of the line perpendicular
to y = –3x + 7?

29. Parallel and Perpendicular Lines
⚫ Nonvertical lines are parallel iff (if and only if) they have
the same slope. Any two vertical lines are parallel.
⚫ Two nonvertical lines are perpendicular iff the product
of their slopes is –1 (negative reciprocals). Vertical and
horizontal lines are perpendicular.
⚫ Example: What is the slope of the line perpendicular
to y = –3x + 7?
−
=
−
1 1
3 3
or just flip –3 and change the sign:
−
→
3 1
1 3

30. Writing the Equation of a Line
⚫ From a graph:
⚫ Calculate the slope
⚫ Select a point on the graph. If the y-intercept is
available, use that by preference.
⚫ Write the equation in either point-slope form or
slope-intercept form.

31. Writing the Equation of a Line
⚫ Ex.: Write the equation of the graph:

32. Writing the Equation of a Line
⚫ Ex.: Write the equation of the graph:
⚫ The y-intercept (b) is –1.
⚫ The slope is up 2, over 3 or .
2
3

33. Writing the Equation of a Line
⚫ Ex.: Write the equation of the graph:
⚫ The y-intercept (b) is –1.
⚫ The slope is up 2, over 3 or .
2
3
= −
2
1
3
y x

34. Writing the Equation of a Line
⚫ Ex.: Write the equation of the graph:
⚫ The y-intercept (b) is –1.
⚫ The slope is up 2, over 3 or .
⚫ To convert to standard form:
2
3
= −
2
1
3
y x
− + = −
2
1
3
x y
( )
 
− − + = − −
 
 
2
3 3 1
3
x y  − =
2 3 3
x y

35. Writing the Equation of a Line
⚫ From a point and a slope:
⚫ Plug into the point-slope form and transform it into
the requested form (slope-intercept or standard) if
necessary.
⚫ From two points:
⚫ Calculate the slope, and pick one point to plug into
the point-slope form.

36. Writing the Equation of a Line
⚫ Example: Write the equation in slope-intercept form for
the line that contains the point (2, –7) and has slope –3.

37. Writing the Equation of a Line
⚫ Example: Write the equation in slope-intercept form for
the line that contains the point (2, –7) and has slope –3.
y – (–7) = –3(x – 2)
y + 7 = –3x + 6
y = –3x – 1

38. Classwork
⚫ College Algebra 2e
⚫ 2.2: 6-20 (even); 2.1: 18-26 (even), 34; 1.6: 34-50
(even)
⚫ 2.2 Classwork Check
⚫ Quiz 2.1