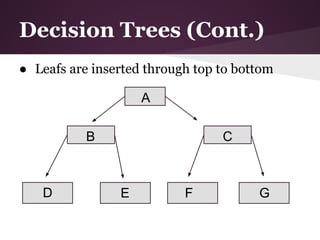
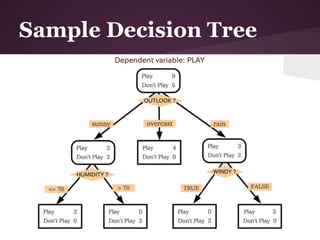
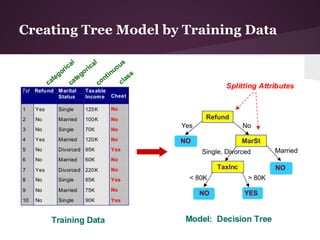
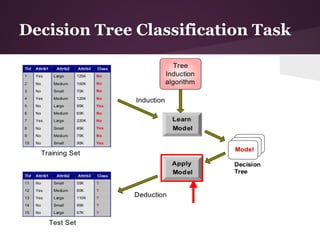
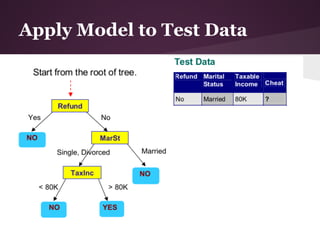
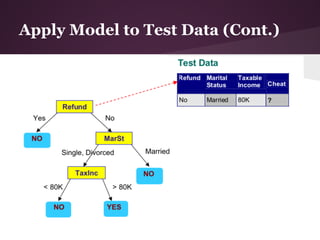
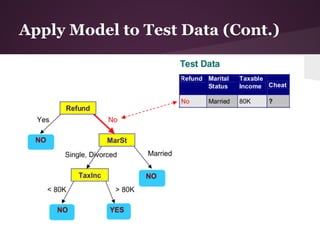
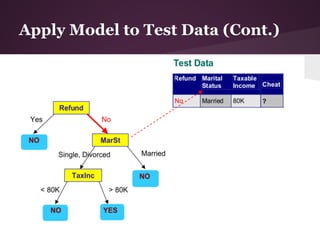
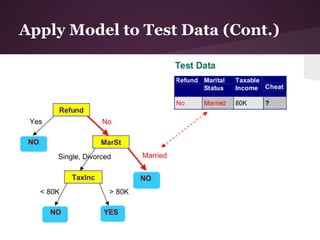
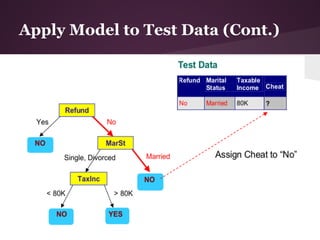
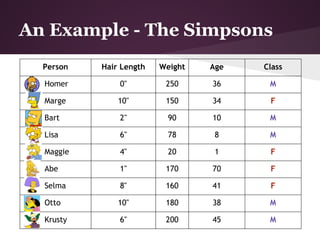
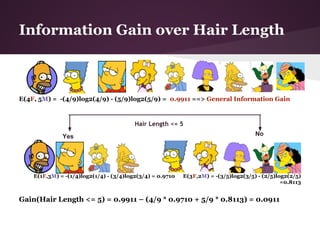
The document discusses decision trees and the ID3 algorithm. It provides an overview of decision trees, describing their structure and how they are used for classification. It then explains the ID3 algorithm, which builds decision trees based on entropy and information gain. The key steps of ID3 are outlined, including calculating entropy and information gain to select the best attributes to split the data on at each node. Pros and cons of ID3 are also summarized. An example applying ID3 to classify characters from The Simpsons is shown.

1. ID3 Algorithm &
ROC Analysis
Talha KABAKUŞ
talha.kabakus@ibu.edu.tr

2. Agenda
● Where are we now?
● Decision Trees
● What is ID3?
● Entropy
● Information Gain
● Pros and Cons of ID3
● An Example - The Simpsons
● What is ROC Analysis?
● ROC Space
● ROC Space Example over predictions

3. Where are we now?

4. Decision Trees
● One of the most used classification approach because of
its clear model and presentation
● Classification by using data attributes
● Aim is to reaching estimating destination field
value using source fields
● Tree Induction
○ Create tree
○ Apply data into tree to classify
● Each branch node represents a choice between a
number of alternatives
● Each leaf node represents a classification or decision
● Leaf Count = Rule Count

5. Decision Trees (Cont.)
● Leafs are inserted through top to bottom
A
B C
D E F G

6. Sample Decision Tree

7. Creating Tree Model by Training Data

8. Decision Tree Classification Task

9. Apply Model to Test Data

10. Apply Model to Test Data (Cont.)

11. Apply Model to Test Data (Cont.)

12. Apply Model to Test Data (Cont.)

13. Apply Model to Test Data (Cont.)

14. Apply Model to Test Data (Cont.)

15. Decision Tree Algorithms
● Classification and Regression
Algorithms
○ Twoig
○ Gini
● Entropy-based Algorithms
○ ID3
○ C4.5
● Memory-based (Sample-based)
Classification Algorithms

16. Decision Trees by Variable Type
● Single Variable Decision Trees
○ Classifications are done with asking
questions over only one variable
● Hybrid Decision Trees
○ Classifications are done with asking
questions over both single and multiple
variables
● Multiple Variables Decision Trees
○ Classifications are done with asking
questions over multiple variables

17. ID3 Algorithm
● Iterative Dichotomizer 3
● Developed by J. Ross Quinlan in 1979
● Based on Entropy
● Only works for discrete data
● Can not work with defective data
● Advantage over Hunt's algorithm is choosing
the right attribute while classification.
(Hunt's algorithm chooses randomly)

18. Entropy
● A formula to calculate the homogeneity of a
sample; gives idea about how much
information gain provides each leaf
● A complete homogeneous sample
entropy value is 0
● An equally divided sample entropy value is 1
● Formula:

19. Information Gain (IG)
● Information Gain calculates effective change
in entropy after making a decision based on
the value of an attribute.
● Which attribute creates the most
homogeneous branches?
● First the entropy of the total dataset is
calculated.
● The dataset is then split on the different
attributes.

20. Information Gain (Cont.)
● The entropy for each branch is calculated.
Then it is added proportionally, to get total
entropy for the split.
● The resulting entropy is subtracted from the
entropy before the split.
● The result is the Information Gain, or
decrease in entropy.
● The attribute that yields the largest IG is
chosen for the decision node.

21. Information Gain (Cont.)
● A branch set with entropy of 0 is a
leaf node.
● Otherwise, the branch needs further
splitting to classify its dataset.
● The ID3 algorithm is run recursively
on the non-leaf branches, until all data
is classified.

22. ID3 Algorithm Steps
function ID3 (R: a set of non-categorical attributes,
C: the categorical attribute,
S: a training set) returns a decision tree;
begin
If S is empty, return a single node with value Failure;
If S consists of records all with the same value for
the categorical attribute,
return a single node with that value;
If R is empty, then return a single node with as value
the most frequent of the values of the categorical attribute
that are found in records of S; [note that then there
will be errors, that is, records that will be improperly
classified];
Let D be the attribute with largest Gain( D,S)
among attributes in R;
Let {dj| j=1,2, .., m} be the values of attribute D;
Let {Sj| j=1,2, .., m} be the subsets of S consisting
respectively of records with value dj for attribute D;
Return a tree with root labeled D and arcs labeled
d1, d2, .., dm going respectively to the trees
ID3(R-{D}, C, S1), ID3(R-{D}, C, S2), .., ID3(R-{D}, C, Sm);
end ID3;

23. Pros of ID3 Algorithm
● Builds decision tree in min. steps
○ The most important point while tree
induction is collecting enough reliable
associated data over specific properties.
○ Asking right questions determines tree
induction.
● Each level benefits from previous level
choices
● Whole dataset is scanned to create tree

24. Cons of ID3 Algorithm
● Tree can not be updated when new
data is classified incorrectly, instead
a new tree must be generated.
● Only one attribute at a time is tested
for making a decision.
● Can not work with defective data
● Can not work with numerical
attributes

25. An Example - The Simpsons
Person Hair Length Weight Age Class
Homer 0'' 250 36 M
Marge 10'' 150 34 F
Bart 2'' 90 10 M
Lisa 6'' 78 8 M
Maggie 4'' 20 1 F
Abe 1'' 170 70 F
Selma 8'' 160 41 F
Otto 10'' 180 38 M
Krusty 6'' 200 45 M

26. Information Gain over Hair Length
E(4F, 5M) = -(4/9)log2(4/9) - (5/9)log2(5/9) = 0.9911 ==> General Information Gain
Hair Length <= 5
Yes No
E(1F,3M) = -(1/4)log2(1/4) - (3/4)log2(3/4) = 0.9710 E(3F,2M) = -(3/5)log2(3/5) - (2/5)log2(2/5)
=0.8113
Gain(Hair Length <= 5) = 0.9911 – (4/9 * 0.9710 + 5/9 * 0.8113) = 0.0911

27. Information Gain over Weight
E(4F, 5M) = -(4/9)log2(4/9) - (5/9)log2(5/9) = 0.9911 ==> General Information Gain
Weight <= 160
Yes No
E(4F,1M) = -(4/5)log2(4/5) - (1/5)log2(1/5) = 0.7219 E(0F,4M) = -(0/4)log2(0/4) - (4/4)log2(4/4) = 0
Gain(Weight<= 160) = 0.9911 – (5/9 * 0.7219 + 4/9 * 0 ) = 0.5900

28. Information Gain over Age
E(4F, 5M) = -(4/9)log2(4/9) - (5/9)log2(5/9) = 0.9911 ==> General Information Gain
Age <= 40
Yes No
E(3F,3M) = -(3/6)log2(3/6) - (3/6)log2(3/6) = 1 E(1F,2M) = -(1/3)log2(1/3) - (2/3)log2(2/3)= 0.9188
Gain(Age z= 40) = 0.9911 – (6/9 * 1 + 3/9 * 0.9183 ) = 0.0183

29. Results
Attribute Information Gain (IG)
Hair Length <= 5 0.0911
Weight <= 160 0.5900
Age <= 40 0.0183
● As seen in the results, weight is the best
attribute to classify these group.

30. Constructed Decision Tree
Weight <= 160
Yes No
Hair Length <= 5
Yes No
Female Male

31. Entropy over Nominal Values
● If an attribute has nominal values:
○ First calculate information gain for each attribute
value
○ Then calculate attribute information gain

32. Example II
IG= -(5/15)log2(5/15)-(10/15)log2(10/15) = ~0.918

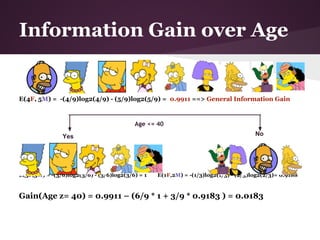
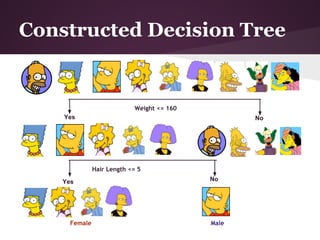
33. Example II (Cont.)
Information Gain over Engine
● Engine: 6 small, 5 medium, 4 large
● 3 values for attribute engine, so we need 3 entropy
calculations
● small: 5 no, 1 yes
○ IGsmall = -(5/6)log2(5/6)-(1/6)log2(1/6) = ~0.65
● medium: 3 no, 2 yes
○ IGmedium = -(3/5)log2(3/5)-(2/5)log2(2/5) = ~0.97
● large: 2 no, 2 yes
○ IGlarge = 1 (evenly distributed subset)
=> IGEngine = IE(S) – [(6/15)*IGsmall + (5/15)*IGmedium +
(4/15)*Ilarge]
= IGEngine = 0.918 – 0.85 = 0.068

34. Example II (Cont.)
Information Gain over SC/Turbo
● SC/Turbo: 4 yes, 11 no
● 2 values for attribute SC/Turbo, so we need 2 entropy
calculations
● yes: 2 yes, 2 no
○ IGturbo = 1 (evenly distributed subset)
● no: 3 yes, 8 no
○ IGnoturbo = -(3/11)log2(3/11)-(8/11)log2(8/11) = ~0.84
IGturbo = IE(S) – [(4/15)*IGturbo + (11/15)*IGnoturbo]
IGturbo = 0.918 – 0.886 = 0.032

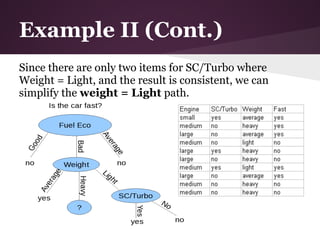
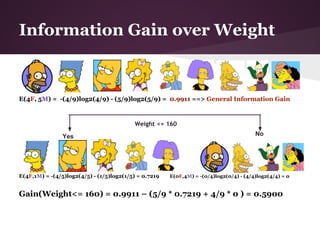
35. Example II (Cont.)
Information Gain over Weight
● Weight: 6 Average, 4 Light, 5 Heavy
● 3 values for attribute weight, so we need 3 entropy
calculations
● average: 3 no, 3 yes
○ IGaverage = 1 (evenly distributed subset)
● light: 3 no, 1 yes
○ IGlight = -(3/4)log2(3/4)-(1/4)log2(1/4) = ~0.81
● heavy: 4 no, 1 yes
○ IGheavy = -(4/5)log2(4/5)-(1/5)log2(1/5) = ~0.72
IGWeight = IE(S) – [(6/15)*IGaverage + (4/15)*IGlight + (5/15)*IGheavy]
IGWeight = 0.918 – 0.856 = 0.062

36. Example II (Cont.)
Information Gain over Full Eco
● Fuel Economy: 2 good, 3 average, 10 bad
● 3 values for attribute Fuel Eco, so we need 3 entropy
calculations
● good: 0 yes, 2 no
○ IGgood = 0 (no variability)
● average: 0 yes, 3 no
○ IGaverage = 0 (no variability)
● bad: 5 yes, 5 no
○ IGbad = 1 (evenly distributed subset)
We can omit calculations for good and average since they always
end up not fast.
IGFuelEco = IE(S) – [(10/15)*IGbad]
IGFuelEco = 0.918 – 0.667 = 0.251

37. Example II (Cont.)
● Results:
IGEngine 0.068
■ Root of the tree
IGturbo 0.032
IGWeight 0.062
IGFuelEco 0.251

38. Example II (Cont.)
● Since we selected the Fuel Eco attribute for our Root Node, it
is removed from the table for future calculations.
General Information Gain = 1 (Evenly distributed set)

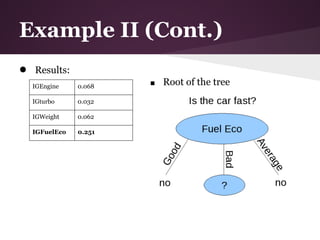
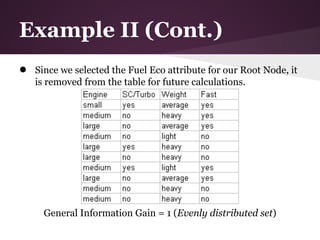
39. Example II (Cont.)
Information Gain over Engine
● Engine: 1 small, 5 medium, 4 large
● 3 values for attribute engine, so we need 3 entropy calculations
● small: 1 yes, 0 no
○ IGsmall = 0 (no variability)
● medium: 2 yes, 3 no
○ IGmedium = -(2/5)log2(2/5)-(3/5)log2(3/5) = ~0.97
● large: 2 no, 2 yes
○ IGlarge = 1 (evenly distributed subset)
IGEngine = IE(SFuelEco) – (5/10)*IGmedium + (4/10)*IGlarge]
IGEngine = 1 – 0.885 = 0.115

40. Example II (Cont.)
Information Gain over SC/Turbo
● SC/Turbo: 3 yes, 7 no
● 2 values for attribute SC/Turbo, so we need 2 entropy calculations
● yes: 2 yes, 1 no
○ IGturbo = -(2/3)log2(2/3)-(1/3)log2(1/3) = ~0.84
● no: 3 yes, 4 no
○ IGnoturbo = -(3/7)log2(3/7)-(4/7)log2(4/7) = ~0.84
IGturbo = IE(SFuelEco) – [(3/10)*IGturbo + (7/10)*IGnoturbo]
IGturbo = 1 – 0.965 = 0.035

41. Example II (Cont.)
Information Gain over Weight
● Weight: 3 average, 5 heavy, 2 light
● 3 values for attribute weight, so we need 3 entropy calculations
● average: 3 yes, 0 no
○ IGaverage = 0 (no variability)
● heavy: 1 yes, 4 no
○ IGheavy = -(1/5)log2(1/5)-(4/5)log2(4/5) = ~0.72
● light: 1 yes, 1 no
○ IlGight = 1 (evenly distributed subset)
IGEngine = IE(SFuel Eco) – [(5/10)*IGheavy+(2/10)*IGlight]
IGEngine = 1 – 0.561 = 0.439

42. Example II (Cont.)
● Results:
IGEngine 0.115
IGturbo 0.035
IGWeight 0.439
Weight has the highest gain, and is thus the
best choice.

43. Example II (Cont.)
Since there are only two items for SC/Turbo where
Weight = Light, and the result is consistent, we can
simplify the weight = Light path.

44. Example II (Cont.)
● Updated Table: (Weight = Heavy)
● All cars with large engines in this table are not fast.
● Due to inconsistent patterns in the data, there is no way to
proceed since medium size engines may lead to
either fast or not fast.

45. ROC Analysis
● Receiver Operating Characteristic
● The limitations of diagnostic “accuracy” as a measure
of decision performance require introduction of the
concepts of the “sensitivity” and “specificity” of a
diagnostic test. These measures and the related
indices, “true positive rate” and “false positive
rate”, are more meaningful than “accuracy”.
● ROC curve is shown to be a complete description of
this decision threshold effect, indicating all possible
combinations of the relative frequencies of the various
kinds of correct and incorrect decisions.

46. ROC Analysis (Cont.)
● Combinations of correct & incorrect decisions:
Actual Value Prediction Outcome Description
p p True Positive Rate (TPR)
p n False Negative Rate (FNR)
n p False Positive Rate (FPR)
n n True Negative Rate (TNR)
● TPR is equivalent with sensitivity.
● FPR is equivalent with 1 - specificity.
● Best possible prediction would be 100% sensitivity
and 100% specificity (which means FPR = 0%).

47. ROC Space
● A ROC space is defined by FPR and TPR as x
and y axes respectively, which depicts relative
trade-offs between true positive (benefits) and
false positive (costs).
● Since TPR is equivalent with sensitivity and
FPR is equal to 1 − specificity, the ROC graph
is sometimes called the sensitivity vs (1 −
specificity) plot.
● Each prediction result one point in the ROC
space.

48. Calculations
● Sensitivity
○ TPR = TP / P = TP / (TP + FN)
● Specificity
○ FPR = FP / N = FP / (FP + TN)
● Accuracy
○ ACC = (TP + TN) / (P + N)

49. A ROC Space Example
● Let A, B, C, D to be predictions over 100
negative and 100 positive instance:
Prediction/ TP FP FN TN TPR FPR ACC
Combination
A 63 28 37 72 0.63 0.28 0.68
B 77 77 23 23 0.77 0.77 0.50
C 24 88 76 12 0.24 0.88 0.18
D 76 12 24 88 0.76 0.12 0.82

50. A ROC Space Example (Cont.)

51. References
1. Data Mining Course Lectures, Ass. Prof. Nilüfer
Yurtay
2. Quinlan, J.R. 1986, Machine Learning, 1, 81
3. http://www.cse.unsw.edu.
au/~billw/cs9414/notes/ml/06prop/id3/id3.html
4. J. Han, M. Kamber, J. Pie, Data Mining Concepts and
Techniques, 3rd Edition, Elsevier, 2011.
5. http://www.cise.ufl.edu/~ddd/cap6635/Fall-
97/Short-papers/2.htm
6. C. E. Metz, Basic Principles of ROC Analysis,
Seminars in Nuclear Medicine, Volume 8, Issue 4, P
283-298