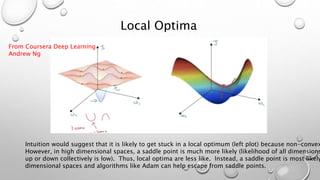
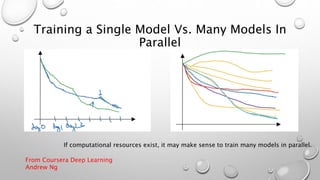
The document discusses hyperparameters and hyperparameter tuning in deep learning models. It defines hyperparameters as parameters that govern how the model parameters (weights and biases) are determined during training, in contrast to model parameters which are learned from the training data. Important hyperparameters include the learning rate, number of layers and units, and activation functions. The goal of training is for the model to perform optimally on unseen test data. Model selection, such as through cross-validation, is used to select the optimal hyperparameters. Training, validation, and test sets are also discussed, with the validation set used for model selection and the test set providing an unbiased evaluation of the fully trained model.

1. DEEP LEARNING WITH
TENSORFLOW
Hyperparameters and Hyperparameter Tuning
Week 3 (Units 4-5)
Jon Lederman

2. Goal Of Training
• We have focused on training (“learning”) algorithms for deep neural networks
• In particular, the backpropagation algorithm
• However, what really matters is how well the network performs at inference time on data it has never
seen
• Inference vs. Training Time
• At inference (prediction) time, the model is flying solo will encounter data it has never seen before!
• The overall goal of training is to arrive at a model that performs optimally at inference time – i.e., on
data in the real world
• Thus, the goal of training is to learn the optimal weights and biases such that the model will perform
optimally on data outside of the training set
• To evaluate the training, we need a data set that the neural network has never seen before
(i.e., during training).
• This is called the test dataset

3. Parameters and Hyperparameters
• Model Parameters
• These are the entities learned via training from the training data. They are not set
manually by the designer.
• With respect to deep neural networks, the model parameters are:
• Weights
• Biases
• Model Hyperparameters
• These are parameters that govern the determination of the model parameters during
training
• They are typically set manually via heuristics
• They are tuned during a cross-validation phase (discussed later)
• Examples:
• Learning rate, number of layers, number of units in each layer, many others to be

4. Machine Learning Models
• What is a model?
• For purposes of this discuss, the Model comprises the hyperparameters characterizing the neural
network. Because hyperparameters govern the parameters of the underlying network, implicitly the
model comprises:
• The topology of the deep neural network (i.e., layers and units and their interconnection)
• The learned parameters (i.e., the learned weights and biases)
• The model is dependent upon the hyperparameters because the hyperparameters determine
the learned parameters (weights and biases).
• Hyperparameters include:
• Learning Rate
• Number of Layers
• Number of Units in each Layer
• Activation Functions
• Capacity – e.g., polynomial degree
• Etc.

5. Model Selection
• To optimize the inference time behavior (the goal of training), a process known as
model selection is performed
• Model selection amounts to selecting an optimal set hyperparameters that yield the best
performance of the neural network
• The hyperparameters are tuned using an iterative process of either:
• Validation
• Cross-Validation
• Many models may be evaluated during the validation/cross-validation phase and the
optimal model is selected
• The optimal model is then evaluated on the test dataset to determine how well it performs on
data never seen before

6. Training, Validation and Test Sets
• Training Set – Data set used to learn the optimal model parameters (weights, biases)
• Validation (“Dev”) Set – Data set used to perform model selection (tuning of hyperparameters)
• Used to estimate the generalization error of the training allowing for the hyperparameters to be
updated accordingly
• Cross-validation set is a variant on validation set (discussed later)
• Test Set – Data set used to assess the fully trained model
• A fully trained model is the model that has been selected via hyperparameter tuning and has been
subsequently been trained to determine the optimal weights and biases (e.g., using backpropagation)
• The test set is not used to perform further training
• Why separate test and validation sets?
• The error rate estimate of the final model on validation data will be biased (smaller than the true error
rate) since the validation set is used to select the model

7. Train, Validation (“Dev”) and Test Sets
Training SetDataset Test Set
Cross-
Validation or
Development
Set
Training of Parameters (weights/biases) Model Selection
(Hyperparameters)
Evaluation of Model
On Unseen Data
Workflow:
1) Train algorithms on training set
2) Use dev set to see which of many different trained models performs
3) Once final model has been found, evaluate it on the test set to get an unbiased estimate on how
algorithm performs

8. The Design Process of Deep Learning
• Iteration
• Tools do not exist to determine the optimal hyperparameters (e.g., learning rate, #
of layers, # of units in each layer, etc.) a priori
• Instead, the optimal choices are determined by experimentation and iteration
From Andrew Ng – Coursera
Deep Learning Course

9. Train, Validation (“Dev”) and Test Sets
Split
Training SetDataset Test Set
Cross-
Validation or
Development
Set
Training of Parameters (weights/biases) Model Selection
(Hyperparameters)
Evaluation of Model
On Unseen Data
• Because we live in era of big data (data is much more prevalent), the trend is to apportion a mu
percentage of data to the dev and test sets (e.g., may have 1*10^6 examples or even more)
• In the past the split was typically: 60%/20%/20%
• Trend: Now a typical example may be 98%/1%/1%

10. Mismatch
• Dev and Test sets should come from same distribution

11. K-Fold Cross-Validation

12. Bias and Variance
• Bias – Error from erroneous assumptions in the learning algorithm. High bias can cause al
algorithm to miss the relevant relations between features and target outputs (underfitting).
• Variance – Error from the sensitivity to small fluctuations in the training set. High variance can
cause an algorithm to model the random noise in the training data, rather than the intended
outputs (overfitting).
• Tradeoff – Goal is to choose a model that accurately captures the regularities in the training
data but also generalizes well to unseen data. Difficult to do both simultaneously.
• Models with low bias are typically more complex (e.g., higher order regression polynomials) enabling
them to represent the training set more accurately. However, in doing so, these models may in fact
capture the noise inherent in the training set making their predictions less accurate on the training set
(unseen data).
• Models with high bias (low-order polynomials) many not be able to capture the higher order (non-
linear) behavior of the daa.

13. Bias and Variance Pictures
From Coursera Deep Learning – Andrew N
high bias “just right” high variance

14. Capacity
• A model’s capacity is its ability to fit a wide variety of functions
• Models with low capacity may fail to fit the training set (underfitting)
• Models with high capacity can overfit by learning properties of the training set that
do not serve well o on the test set such as the noise

15. Bias Variance Decomposition
• Training set of points: 𝑥(1), 𝑥(2). . 𝑥(𝑚)
• Assume function 𝑦 = 𝑓 𝑥 + 𝜀 with noise 𝜀 with 0 mean and variance 𝜎2
• Goal: Find function 𝑓(𝑥) that approximates the true function 𝑓 𝑥 so as to
minimize (𝑦 − 𝑓 𝑥 ) 2
• Note: 𝑉𝑎𝑟 𝑋 = 𝐸 𝑋2 − 𝐸[𝑋]2
• Note: 𝐸[𝜀]=0, 𝐸[𝑦]=𝐸[𝑓 + 𝜀]=𝐸 𝑓 = f
• Note: 𝑉𝑎𝑟 𝑦 = 𝐸 𝑦 − 𝐸 𝑦 2 = 𝐸 𝑦 − 𝑓 2 = 𝐸 𝑓 + 𝜀 − 𝑓 2 =𝜎2

16. Bias Variance Decomposition
𝐸 𝑦 − 𝑓
2
= 𝐸 𝑦2 + 𝑓2 − 2𝑦 𝑓
= 𝐸 𝑦2
+ 𝐸 𝑓2
− 2𝐸[𝑦 𝑓]
= 𝑉𝑎𝑟 𝑦 + 𝐸[𝑦]2 + 𝑉𝑎𝑟 𝑓 + 𝐸[ 𝑓]2 − 2𝑓𝐸[ 𝑓]
= 𝑉𝑎𝑟 𝑦 + 𝑉𝑎𝑟[ 𝑓]+(𝑓2
− 2𝑓𝐸[ 𝑓]+𝐸[ 𝑓2
])
= 𝑉𝑎𝑟 𝑦 + 𝑉𝑎𝑟 𝑓 +(𝑓 − 𝐸[ 𝑓]) 2
𝐸 𝑦 − 𝑓
2
= 𝜎2 + 𝑉𝑎𝑟 𝑓 + 𝐵𝑖𝑎𝑠[ 𝑓]
2
Average test error over large ensemble of training sets

17. Analysis Of Bias-Variance Decomposition
• What is variance?
• Amount that 𝑓 would change if estimated it with a different training set
• Ideally, 𝑓 should not vary much between training sets
• With high variances, small perturbations in training set result in large changes in 𝑓
• What is bias?
• Bias is the error introduced by approximating real-life problems, which may be very
complex.
• For example, the world is highly non-linear and choosing a linear model will result in high
bias.
• In order to minimize the expected test error, need to minimize both bias and
variance

18. High Bias and High Variance
From Coursera Deep Learning – Andrew N
𝑥1
This means in some regions there is high
bias while in others high variance.

19. Bias-Variance Analysis
1. Analyze Training Set Performance (potential underfit)
• If low accuracy on training set data, may have a bias problem
2. Analyze Development/Validation Set Performance
• If low accuracy on development set, may have a variance problem
3. Bias/Variance Tradeoff Less Of An Issue In Big Data Era
1. Bias can be driven down by introducing more capacity (larger network)
1. Training a larger network almost never hurts so long as regularization is employed.
2. Variance can be driven down by obtaining more training data

20. Potential Solutions
High Bias High Variance
Try network with more
capacity (e.g., more
hidden units per layer)
Obtain more training data
Train longer Regularization (to be
discussed)
Try different architecture Try different architecture

21. L2 Regularization
For Neural Network Regularization Term
Frobenius Norm – (Equiv to L2 Norm)

22. L2 Regularization
For Neural Network
From backprop derivation New Term: Weight Decay
Weight Decay
Note: Can also regularize bias terms
But since there are far fewer,
It will have less of an impact.

23. Why L2 Regularization Works
Expand around w* making the approximation of a quadratic cost function.
No first order term b/c it vanishes at minimum.Hessian Matrix
Consider a single neuron with weight vector w
Minimum occurs where:
Now consider gradient of
regularized J:
Express H as eigenvalue/eigenvector
decomposition
After substitution and
some algebra:
Upshot: Component of w* along ith
eigenvector is scaled by:
Lambda without subscript is
regularization parameter.
Lambda with subscript is eigen

24. Why L2 Regularization Works
Upshot: Component of w* along ith
eigenvector is scaled by:
Along directions where 𝜆𝑖 ≫ 𝛼, regularization effects are small.
Along directions where 𝜆𝑖 ≪ 𝛼, regularization will shrink weight to 0.
Only directions along which the parameters contribute significantly to reducing the
objective function are preserved intact. In directions that do not contribute significantly
In reducing the objective function, a small eigenvalue of the Hessian indicates that
Movement in this direction will not significantly increase the gradient.
Components of the weight vector corresponding to such unimportant directions are
decayed through regularization.

25. Why L2 Regularization Works
Another Way To Look at It
• Cranking up 𝜆 effectively zeros out some hidden units by driving W to 0 due to
weight decay, reducing the capacity of the network and thus reduces risk of
overfitting
• Actually all hidden units still used but each has smaller effect

26. L1 Regularization
(Less Common)
Results in sparse model (many parameters
Results in compression

27. Dropout Regularization
Dropout trains an ensemble consisting of all
subnetworks that can be constructed by removing
nonoutput units from an underlying base network.

28. Dropout
For each training example, randomly kill hidden units at training time only

29. Dropout Effect Example

30. Dropout As Regularization
• How does dropout have a regularizing effect?
• By ”killing” units, it reduces the capacity of the network, reducing potential for
overfitting
• By ”killing” units, it makes any neuron unable to “rely” on any one input feature. So,
rather than betting heavily on any one input feature, weights are spread out among
input neurons
• That is, it reduces the weights proportionally among input nodes
• Dropout used heavily in computer vision b/c almost never have enough data
• Key point: Cost function is not well defined b/c killing off nodes on each iteration
• Plotting cost function is thus not meaningful if dropout is employed
• Solution: Turn off dropout and plot cost function to make sure it is working. Then, turn dropout
on.

31. Data Augmentation As Regularization
• Data Augmentation
• Synthetically transform or distort data to generate fake training examples

32. Early Stopping
• When training large models with sufficient representational capacity to overfit,
training error steadily decreases over time but validation error falls but
eventually begins to rise

33. Early Stopping
• Idea: Stop training when validation error is at a minimum (although the cost
function is not)
• Every time the validation set error improves, store the latest set of model parameters
• When training terminates, return the model parameters with the lowest validation set error
and the hyperparameter indicating the number of iterations
• View the number of training iterations as a hyperparameter 𝜏 to be tuned
• Problem: This technique breaks orthogonality of training and validation (hyperparameter
selection) phases
• Complicates optimization

34. Early Stopping Equivalent To L2
Regularization
• It can be shown that the product 𝛼𝜏 is a measure of the capacity of the network
• The product 𝛼𝜏 behaves as if it were the reciprocal of the coefficient of weight decay
• From before:
Exercise, show for small eigenvalues 𝜆𝑖 of the Hessian matrix:
𝜏 plays a role inverse to the L2 regularization parameter 𝜆
1
𝜏𝛼
plays a role equivalent to the weight decay coefficient
Hint: Use eigenvalue decomposition as before

35. Why Learning Can Be Slow
If ellipse is very elongated (will happen if
lines corresponding to two training
examples are almost parallel), steepest
descent can be very slow. This is due to
the fact that with an elongated ellipse,
the gradient is big in the direction in
which we don’t want to move very far
and small in direction where we would
like to move a long way. This condition
will cause the trajectory across the
ravine rather than along the ravine. This
is the opposite of the desired goal.
*From Neural Networks For Machine Learning (Coursera – Hinton)

36. Why Learning Can Be Slow
From Coursera
Deep Learning
Andrew Ng

37. Normalization Of Inputs
• Subtract Mean
• 𝜇 =
1
𝑚 𝑖=1
𝑚
𝑥(𝑖)
• 𝑥 = 𝑥 − 𝜇
• Normalize Variance
• 𝜎2
=
1
𝑚 𝑖=1
𝑚
𝑥𝑖
2
• 𝑥 =
𝑥
𝜎2

38. Vanishing and Exploding Gradients
Observation: The rate at which individual neurons in different layers learn varies greatly

39. Review: Backpropagation With Gradient
Descent
• For each training example x, set the input activation 𝒂[0](𝑥) and perform the
following steps:
• Feedforward: For each l=1, 2, 3, … L compute 𝒛[𝑙](𝑥) = 𝒘[𝑙] 𝒂 𝑙−1 (𝑥) + 𝒃[𝑙] and 𝒂[𝑙](𝑥) =
𝜎(𝒛 𝑙
)
• Output Error: Compute 𝜺[𝐿](𝑥) = 𝜵 𝒂 𝐽⨀𝜎′(𝒛[𝐿](𝑥))
• Backpropagate Error: For each i=L-l, L-2 , … 1 compute 𝜺[𝑙](𝑥) =
((𝒘[𝑙+1]) 𝑇 𝜺[𝑙+1](𝑥))⨀𝜎′(𝒛[𝑙](𝑥))
• Compute One Step Of Gradient Descent: For each l=L, L-1, L-2, … 1, update the
weights according to the rules:
• 𝒘𝑙
= 𝒘𝑙
−
∝
𝑚 𝑥 𝜺 𝑙 𝑥
(𝒂 𝑙−1 𝑥
) 𝑇
• 𝒃𝑙
= 𝒃𝑙
−
𝛼
𝑚 𝑥 𝜺 𝑙 𝑥
Controls how fast learning occurs for 𝒘𝑙
Controls how fast learning occurs for 𝒃𝑙

40. Review: The 4 Fundamental Equations Of
Backpropagation And Their Interpretation
(1)
(2)
(3)
(4)
Calculate error of
last layer
Propagate error
backwards preceding
layers
Calculate gradient
of cost function with
respect to weights using
errors
Calculate gradient
of cost function with
respect to biases
using errors

41. Vanishing and Exploding Gradients
Consider the backpropagation equation for computing the gradient with respect to w:
where
As we propagate backwards, for each layer we introduce addit
factor of 𝑤𝑗 𝜎′𝑗

42. Vanishing and Exploding Gradients
Consider the backpropagation equation for computing the gradient with respect to w:
Consider eigen-decomposition of weight
matrix:
For eigenvalues 𝜆𝑖<1 – vanishing gradients
For eigenvalues 𝜆𝑖 >1 – exploding gradients
Vanishing gradients makes learning slow and due to numerical instability confuses direction of grad
Exploding gradients leads to instability.

43. Partial Solution to Vanishing Exploding
Gradients
• Random initialization of neurons to optimal value not too much less than and
not too much larger than 1
• Then, gradients won’t explode or vanish too quickly
• Some Rules of Thumb:
• Set variance for each neuron 𝜎2
=
1
𝑛
where n is the number of input features for the neuron
• For ReLu activation functions set variance for each neuron 𝜎2
=
2
𝑛
where n is the number of
input features for the neuron
• For Tanh set variance 𝜎2
=
1
𝑛 𝑙−1

44. Mini-Batch Gradient Descent
• Vectorization allows efficient computation on m training examples
• However, this results in slow progress as all m examples must be processed before
progress can be made
• This is especially apparent if m is large
• What is there were a way to make progress before processing all m examples?

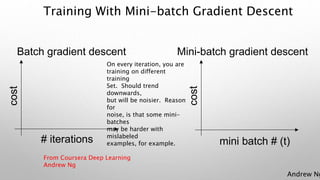
45. Mini-Batch Gradient Descent
• Solution:
• Divide training set into smaller mini-batches:
• 𝑿 = [𝑋1
, 𝑋2
, 𝑋3
, . . . 𝑋 𝑏
| 𝑋 𝑏+1
, 𝑋 𝑏+2
, 𝑋 𝑏+3
, . . . 𝑋2𝑏
|. . . 𝑋 𝑚−1 𝑏+1
… 𝑋 𝑚
• 𝒀 = [𝑌1
, 𝑌2
, 𝑌3
, . . . 𝑌 𝑏
| 𝑌 𝑏+1
, 𝑌 𝑏+2
, 𝑌 𝑏+3
, . . . 𝑌2𝑏
|. . . |𝑌 𝑚−1 𝑏+1
… 𝑌 𝑚
]
• Each 𝑿{𝑖}
has dimension (nx, b)
• Each 𝒀{𝑖}
has dimension (1, b)
𝑿{1}
𝑿{2} 𝑿{𝑚/𝑏}
𝒀{1}
𝒀{1} 𝒀{𝑚/𝑏}

46. Nomenclature For Batch Size
• Batch Gradient Descent – Process entire batch (i.e., m training examples) at
same time
• Mini-Batch Gradient Descent – Process a single mini-batch of (i.e., b training
examples) at same time

47. Mini-Batch Gradient Descent
Pseudo-Code
For j=1. . .E (number of epochs)
For t=1 …b{
Forward prop on 𝑿{𝑡}
𝒁[1]
= 𝑾[1]
𝑿{𝑡}
+ 𝒃[1]
𝑨[1]
= 𝒈 1
𝒁 1
…
𝑨[𝐿]
= 𝒈 𝐿
𝒁 𝐿
𝐽{𝑡}
=
1
𝑏 𝑖=1
𝑏
𝐿( 𝒚 𝑖
, 𝒚 𝑖
)+
𝜆
2∗𝑏 𝑙 ||𝒘𝑙
2
|| 𝐹
Backpropagation to compute gradients with respect to 𝐽{𝑡}
𝒘𝑙
= 𝒘𝑙
-𝛼𝑑𝒘𝑙
𝒃𝑙
= 𝒃𝑙
-𝛼𝑑𝒃𝑙
}
}
1 epoch

48. Andrew Ng
Training With Mini-batch Gradient Descent
# iterations
cost
Batch gradient descent
mini batch # (t)
cost
Mini-batch gradient descent
From Coursera Deep Learning
Andrew Ng
On every iteration, you are
training on different
training
Set. Should trend
downwards,
but will be noisier. Reason
for
noise, is that some mini-
batches
may be harder with
mislabeled
examples, for example.

49. Mini-Batch Sizes
• If b=m, this reduces to batch gradient descent. 𝑿{1}, 𝒀{1} = (𝑿, 𝒀)
• Disadvantage – Progress is slow. Need to wait until entire training set is processed
for each update.
• If b=1, this is called stochastic gradient descent (“SGD”). 𝑿{1}
, 𝒀{1}
= (𝑿(1)
, 𝒀(1)
),
etc.
• Disadvantage – Lose all of speedup due to vectorization!
• If 1 < 𝑏 < 𝑚, this is mini-batch gradient descent
• There will be one mini-batch size that works best. Mini-batch size is a
hyperparameter.
• If small batch size is small:
• Use batch gradient descent
• Mini-batch size is typically a power of 2
• Make sure that mini-batch can fit in CPU/GPU memory otherwise performance uffer.

50. Comparing Convergence RE: Batch Sizes
Batch Gradient Descent
Mini-batch Gradient Descent
Stochastic Gradient Descent
From Coursera Deep
Learning
Andrew Ng

51. Exponential Smoothing
(Exponential Weighted Average)
• 𝑉𝑡 = 𝛽𝑉𝑡−1 + (1 − 𝛽)𝜃𝑡 where 𝜃𝑡 is a time series
• 0 < 𝛽 < 1
• 𝑉𝑡 is approximately an average over
1
1−𝛽
time steps
From Coursera Deep
Learning
Andrew Ng
𝛽 = 0.9
𝛽 = 0.98
𝛽 = 0.5

52. Exponential Smoothing
(Exponential Weighted Average)
• Weights are proportional to the terms of the geometric progression:
{1, 𝛽, 𝛽2, 𝛽3. . . }
• To determine roughly how large the window is in time steps solve: 𝛽 𝑇 =
1
𝑒
and
solve for T, where T is the number of time steps
• Bias Correction:
• In early phase of learning set:
𝑉𝑡
1−𝛽 𝑡 to correct for errors in ”warming up”

53. Why Learning Can Be Slow
Review
If ellipse is very elongated (will happen if
lines corresponding to two training
examples are almost parallel), steepest
descent can be very slow. This is due to
the fact that with an elongated ellipse,
the gradient is big in the direction in
which we don’t want to move very far
and small in direction where we would
like to move a long way. This condition
will cause the trajectory across the
ravine rather than along the ravine. This
is the opposite of the desired goal.
*From Neural Networks For Machine Learning (Coursera – Hinton)

54. Gradient Descent Example
If use a large learning rate, oscillations can be large preventing convergence. So, this requires
a small learning rate limiting the speed of learning.
Want fast learning
rate in horizontal
direction to
aggressively move
toward minimum.
Want slow learning
rate in vertical
direction to
prevent
oscillations.

55. Gradient Descent With Momentum
• Solution: Compute exponentially weighted average of the derivatives
• In vertical direction this will zero out the oscillations because average to close to 0
• In horizontal direction (because no oscillations) – all derivatives in same direction
• 𝑉𝑑𝑤 = 𝛽𝑉𝑑𝑤 + 1 − 𝛽 𝑑𝑊
• 𝑉𝑑𝑏 = 𝛽𝑉𝑑𝑏 + 1 − 𝛽 𝑑𝑏
• 𝑤 = 𝑤 − 𝛼𝑉𝑑𝑤
• 𝑏 = 𝑏 − 𝛼𝑉𝑑𝑏

56. Gradient Descent With Momentum
Physics Analogy
Acceleration
Assume unit mass so velocity= momentum
Momentum
Friction
J can be viewed as the negative of the Hamiltonian of the system!
Hamilton’s Equations

57. Nesterov Momentum
• Difference with standard momentum:
• With Nesterov Momentum, the gradient is applied AFTER the current velocity is
applied
• Nesterov Momentum can be interpreted as adding a correction factor to the standard
momentum method
• Brings rate of convergence of excess error from Ο(
1
𝑘
) to Ο
1
𝑘2 after k steps

58. Gradient Descent Example
Review
If use a large learning rate, oscillations can be large preventing convergence. So, this requires
a small learning rate limiting the speed of learning.
Want fast learning
rate in horizontal
direction to
aggressively move
toward minimum.
Want slow learning
rate in vertical
direction to
prevent
oscillations.

59. RMSProp
• Solution: Compute exponentially weighted average of the derivatives
• In vertical direction this will zero out the oscillations because average to close to 0
• In horizontal direction (because no oscillations) – all derivatives in same direction
• 𝑆 𝑑𝑤 = 𝛽𝑆 𝑑𝑤 + 1 − 𝛽 𝑑𝑊2
• 𝑆 𝑑𝑏 = 𝛽𝑉𝑑𝑏 + 1 − 𝛽 𝑑𝑏2
• 𝑤 = 𝑤 − 𝛼
𝑑𝑊
𝑆 𝑑𝑤+𝜖
• 𝑏 = 𝑏 − 𝛼
𝑑𝑏
𝑆 𝑑𝑏+𝜖
RMS terms control damping of oscillations.
Larger values cause oscillations to be damped more.
Can therefore use a faster learning rate and reduce
risk of oscillations. Epsilon term is a small value that
insures numerical stability (i.e., no divide by 0).

60. Adam (Adaptive Moment Estimation)
Combines Momentum with RSMProp
Momentum
RMSProp
Bias Correction
Parameter Update

61. Adam
Hyperparameters
• 𝛼 (needs to be tuned)
• 𝛽1 default from paper = 0.9
• 𝛽2 default from paper = 0.999
• 𝜖 default from paper = 10−8

62. Learning Rate Decay
As converge to minimum, decrease learning rateFrom Coursera Deep Learning
Andrew Ng

63. Learning Rate Decay
(Options)
As converge to minimum, decrease learning rate
Hyperparameter
Hyperparameter
Exponential Decay:
Many other options as well…

64. Local Optima
Intuition would suggest that it is likely to get stuck in a local optimum (left plot) because non-convex
However, in high dimensional spaces, a saddle point is much more likely (likelihood of all dimensions
up or down collectively is low). Thus, local optima are less like. Instead, a saddle point is most likely
dimensional spaces and algorithms like Adam can help escape from saddle points.
From Coursera Deep Learning
Andrew Ng

65. Plateaus
Plateaus are highly likely. They are regions in which the derivative is close to 0 for a long time.
Algorithms like Adam can help escape plateaus.
From Coursera Deep Learning
Andrew Ng

66. Impact Of Some Hyperparameters
(Rules of Thumb)
• 𝛼 – Learning Rate
• 𝛽 – Momentum Parameter
• Number of Hidden Units
• Mini-Batch Size
• Number of Layers
• Learning Rate Decay
• 𝛽1, 𝛽2, 𝜖 – Adam Parameters
Typically Most Important
Middle Importance
Less Important

67. Sampling Scheme
Choose Random Sampling
Uniform Sampling Random Sampling
Some hyperparameters won’t matter much and others will.
Allows exploring range of hyperparameters more quickly.

68. Sampling Scheme
Coarse To FineOnce range has been determined
limit search area to smaller regions.
Coarse to fine.

69. Sampling Scale
Some Tips
• If range is large and/or parameter is very sensitive to small changes, use a log
scale rather than linear scale.
• Then sample uniformly over log value
• For momentum parameter 𝛽, use 1 − 𝛽 and then use a log scale

70. Training a Single Model Vs. Many Models In
Parallel
If computational resources exist, it may make sense to train many models in parallel.
From Coursera Deep Learning
Andrew Ng

71. Review Why Learning Can Be Slow
From Coursera
Deep Learning
Andrew Ng

72. Batch Normalization Motivation
• Subtract Mean
• 𝜇 =
1
𝑚 𝑖=1
𝑚
𝑥(𝑖)
• 𝑥 = 𝑥 − 𝜇
• Normalize Variance
• 𝜎2
=
1
𝑚 𝑖=1
𝑚
𝑥𝑖
2
• 𝑥 =
𝑥
𝜎2
This works fine for simple model
like:
But what about a deeper model like:

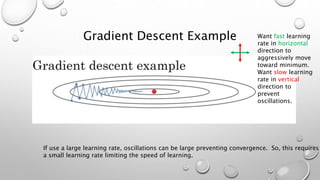
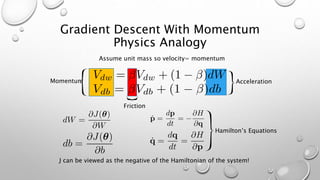
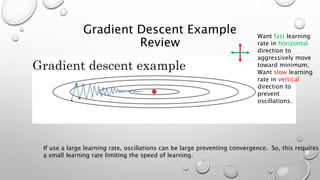
73. Batch Motivation Concept
What if we could normalize the activations: 𝒂[𝑙] so that the training of 𝑾[𝑙+1] and 𝒃[𝑙+1] is more e
That is, can we normalize the activations in the hidden layers too such that training of paramet
layers may happen more rapidly?
In practice, 𝒛𝑙 is normalized.

74. Implementing Batch Normalization
Given weighted sums: 𝒛[𝑙](1)
, 𝒛[𝑙](2)
. . . 𝒛[𝑙](𝑚)
Subtract Mean
𝒛(𝑖)
=
1
𝑚
𝑖=1
𝑚
𝒛(𝑖)
Normalize Variance
𝒖 =
1
𝑚
𝑖
𝒛(𝑖)
𝜎2 =
1
𝑚
𝑖=1
𝑚
(𝒛 𝑖 − 𝝁 𝑖 )2
𝒛 𝑛𝑜𝑟𝑚
(𝑖)
=
𝒛(𝑖)
− 𝝁
𝜎2 + 𝜖
𝒛(𝑖)
= 𝛾 𝒛 𝑛𝑜𝑟𝑚
(𝑖)
+𝛽
This will have mean 0 and variance 1.
But, we don’t always want that. For
example, we may want to cluster
values near non-linear region of
activation function to take advantage
of non-linearity.
𝛾 and 𝛽 are learnable parameters learned
via gradient descent for example.
If 𝛾 = 𝜎2 + 𝜖
and 𝛽 = 𝜇:
𝒛(𝑖)
= 𝒛(𝑖)
𝛾 and 𝛽 control mean and varian

75. Batch Normalization In Neural Network
. . .

76. Notes on Batch Normalization
• Batch normalization is done over mini-batches
• 𝒛[𝑙] = 𝑾[𝑙−1] 𝒛[𝑙] + 𝑏[𝑙]
• 𝛽[𝑙]
𝑎𝑛𝑑 𝛾[𝑙]
have dimensions (𝑛[𝑙]
, 1)
Will be set to 0 in mean subtraction step so we can eliminate b
as parameter. Beta effectively replaces b.

77. Batch Normalization PseudoCode
• For t=1…Number of Mini-Batches
• Compute forward prop on each 𝑋{𝑡}
• In each hidden layer use batch normalization to compute 𝒛[𝑙]
from 𝒛[𝑙]
• Use backpropagation to compute 𝑑𝑾[𝑙]
, 𝑑𝛽[𝑙]
, 𝑑𝛾[𝑙]
• Update parameters:
• 𝑾[𝑙]
= 𝑾[𝑙]
− 𝛼𝑑𝑾[𝑙]
• 𝛽[𝑙]
= 𝛽[𝑙]
− 𝛼𝑑𝛽[𝑙]
• 𝛾[𝑙]
= 𝛾[𝑙]
− 𝛼𝑑𝛾[𝑙]
This will work with momentum, RMSProp and Adam for example.

78. Why Batch Normalization Works
• Similar to input normalization, batch normalization normalizes directions of
slow learning for hidden layers, which allows a higher learning rate to be used
without risk oscillations
• Makes weights deeper in network more robust to weights earlier in the network

79. Covariant Shift
• Covariate shift means that there has been a shift (change) in the training and
test distributions
Prediction on the learned function will generate incorrect results at inference time.
Need to retrain!

80. Covariant Shift and Batch Normalization
Batch normalization limits the amount of shift in the distribution of the input to any hidden layer.
Reduces the amount that updating parameters in earlier layers can affect the distribution in later l
Weakens coupling between earlier and later parameters. This speeds up learning.

81. Batch Normalization As Regularization
• Each mini-batch is scaled by the mean/variance computed on just that mini-
batch
• Thus scaling from 𝒛𝑙 → 𝒛𝑙 is noisy within that mini-batch. Noise is due to the fact
that the mini-batch does not represent the full distribution of the entire batch.
• Similar to dropout, which introduces noise due to random “killing” of neurons
• Forces downstream hidden units not to rely fully on any upstream unit so that unit cannot
contribute too much
• This introduction of noise has a slight regularization effect

82. Batch Normalization At Test Time
Subtract Mean
𝒛(𝑖)
=
1
𝑚
𝑖=1
𝑚
𝒛(𝑖)
Normalize Variance
𝒖 =
1
𝑚
𝑖
𝒛(𝑖)
𝜎2 =
1
𝑚
𝑖=1
𝑚
(𝒛 𝑖 − 𝝁 𝑖 )2
𝒛 𝑛𝑜𝑟𝑚
(𝑖)
=
𝒛(𝑖)
− 𝝁
𝜎2 + 𝜖
𝒛(𝑖)
= 𝛾 𝒛 𝑛𝑜𝑟𝑚
(𝑖)
+𝛽
Problem: 𝝁 and 𝜎2
are computed based on mini-batch
during training.
At test time, we don’t have access to 𝝁 and 𝜎2 as typically
a prediction is made on a single input at at time.
Solution: Compute 𝝁 and 𝜎2
using mini-batches using
Exponentially weighted average.
Compute exponentially weighted average for each layer l,
across mini-batches. Use the last computed exponentially
weighted average at test time.

83. Multiclass Classification
3 Classes
C=Number of Classes
Softmax
Activation
Function
Can prove if C=2, Softmax reduces to logistic regression

84. Softmax Activation Function
This will be a vector of probabilities that sums to 1

85. Softmax Activation Function
(No Hidden Layer – Linear)
From Coursera
Deep Learning
Andrew Ng
Deeper network will allow for non-linear decision boundaries

86. Softmax Loss Function
Cross-Entropy Loss
This is a maximum likelihood estimation (“MLE”)
(C, m) dimensional matrix
Vectorization across training
examples:

87. Softmax Exercise