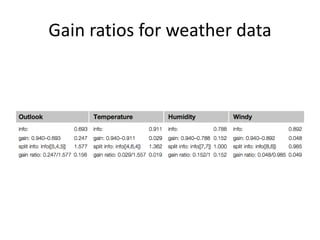
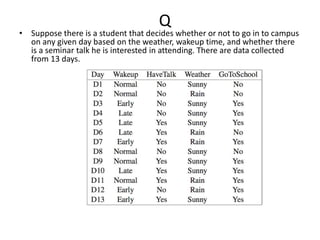
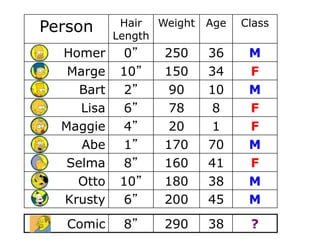
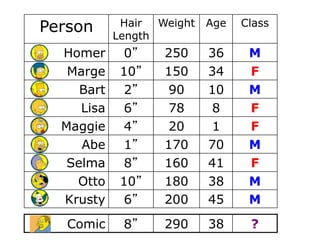
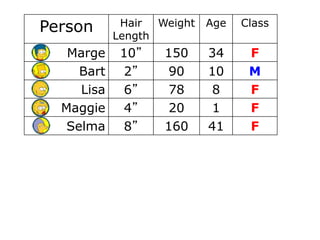
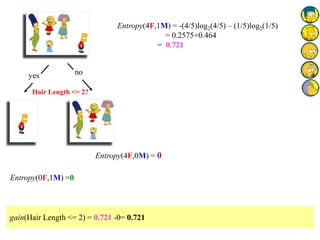
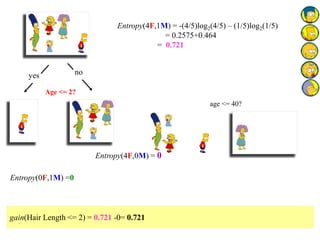
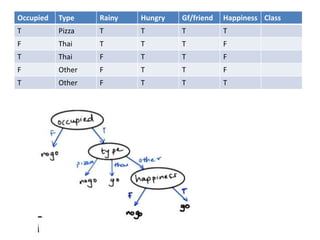
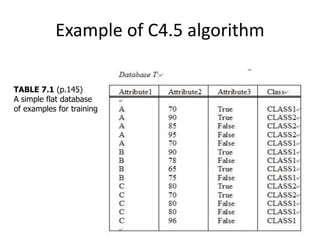
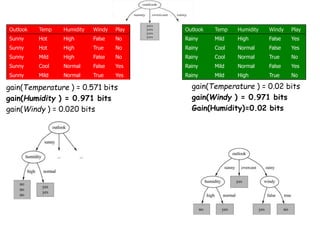
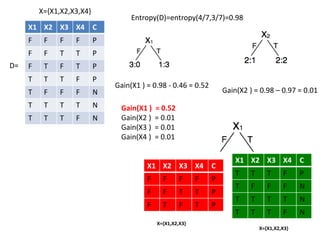
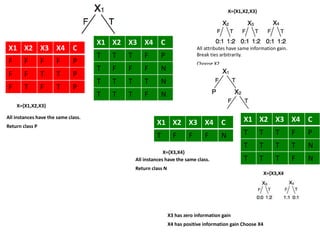
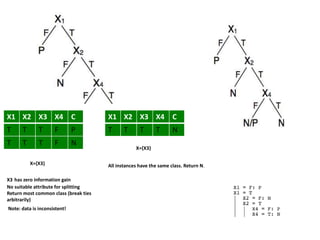
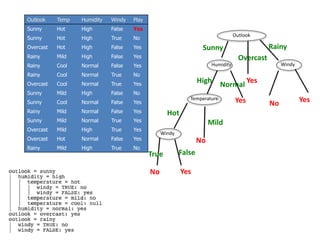
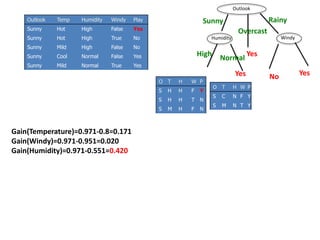
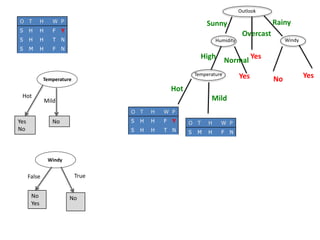
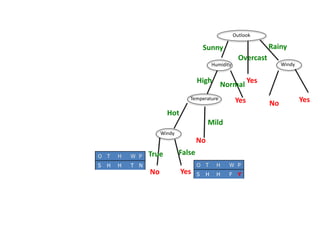
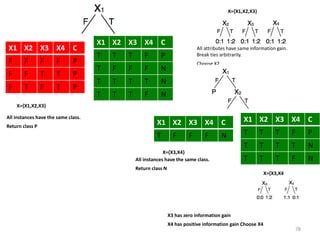
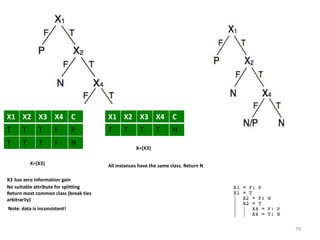
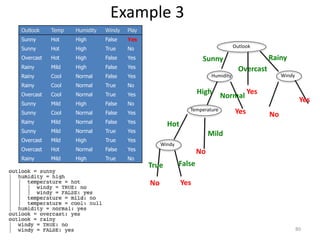
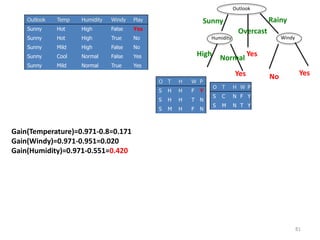
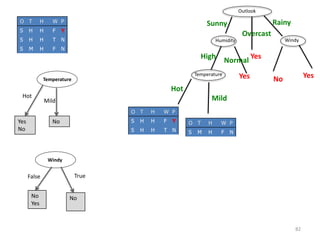
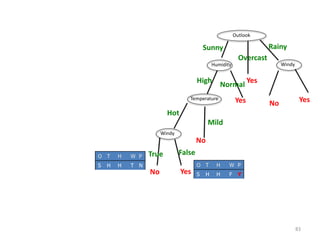
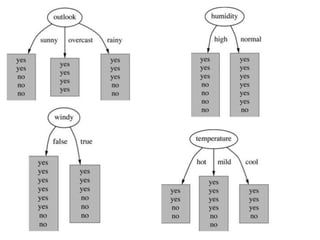
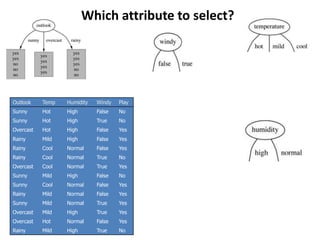
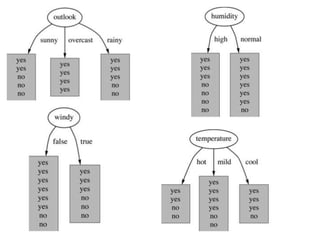
Decision trees are a machine learning technique that use a tree-like model to predict outcomes. They break down a dataset into smaller subsets based on attribute values. Decision trees evaluate attributes like outlook, temperature, humidity, and wind to determine the best predictor. The algorithm calculates information gain to determine which attribute best splits the data into the most homogeneous subsets. It selects the attribute with the highest information gain to place at the root node and then recursively builds the tree by splitting on subsequent attributes.

1. Tilani Gunawardena
Algorithms: Decision Trees

3. Decision Tree
• Decision tree builds classification or regression models in the
form of a tree structure
• It breaks down a dataset into smaller and smaller subsets while
at the same time an associated decision tree is incrementally
developed
• The final results is a tree with decision nodes and leaf notes.
– Decision nodes(ex: Outlook) has two or more branches(ex: Sunny,
Overcast and Rainy)
– Leaf Node(ex: Play=Yes or Play=No)
– Topmost decision node in a tree which corresponds to the best
predictor called root node
• Decision trees can handle both categorical and numerical data

4. Decision tree learning Algorithms
• ID3 (Iterative Dichotomiser 3)
• C4.5 (successor of ID3)
• CART (Classification And Regression Tree)
• CHAID (CHi-squared Automatic Interaction
Detector). Performs multi-level splits when
computing classification trees)
• MARS: extends decision trees to handle
numerical data better.

5. How it works
• The core algorithm for building decisions tress
called ID3 by J.R. Quinlan which employs a
top-down, greedy search through the space of
possible branches with no backtracking
• ID3 uses Entropy and information Gain to
construct a decision tree

6. DIVIDE-AND-CONQUER(CONSTRUCTING
DECISION TREES
• Divide and Conquer approach (Strategy: top
down)
– First: select attribute for root node : create branch
for each possible attribute value
– Then: split instances into subsets ; One for each
branch extending from the node
– Finally: repeat recursively for each branch, using
only instances that reach the branch
• Stop if all instances have same class

7. Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Overcast Hot High False Yes
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Overcast Cool Normal True Yes
Sunny Mild High False No
Sunny Cool Normal False Yes
Rainy Mild Normal False Yes
Sunny Mild Normal True Yes
Overcast Mild High True Yes
Overcast Hot Normal False Yes
Rainy Mild High True No
Which attribute to select?

9. Criterion for attribute selection
• Which is the best attribute?
– The one which will result in the smallest tree
– Heuristic: choose the attribute that produces the “purest” nodes
• Need a good measure of purity!
– Maximal when?
– Minimal when?
• Popular impurity criterion: Information gain
– Information gain increases with the average purity of the subsets
• Measure information in bits
– Given a probability distribution, the info required to predict an event is
the distribution’s entropy
– Entropy gives the information required in bits (can involve fractions of
bits!)
• Formula for computing the entropy:
– Entropy(p1,p2,...,pn)=−p1logp1−p2 logp2...−pnlogpn
Purity measure of each
node improves the
feature/attribute
selection

10. 10
Entropy: a common way to measure impurity
• Entropy =
pi is the probability of class i
Compute it as the proportion of class i in the set.
• Entropy comes from information theory. The higher
the entropy the more the information content.

i
ii pp 2log
Entropy aims to answer “how uncertain we are of the outcome?”

11. Entropy
• A decision tree is built top-down from root node and involves
partitioning the data into subsets that contain instances with
similar values(homogeneous)
• ID3 algorithm uses entropy to calculate the homogeneity of a
sample
• If the sample is completely homogeneous the entropy is zero and
if the samples is an equally divided it has entropy of one

12. 12
2-Class Cases:
• What is the entropy of a group in which all
examples belong to the same class?
– entropy =
• What is the entropy of a group with 50%
in either class?
– entropy =
Minimum
impurity
Maximum
impurity

i
ii pp 2logEntropy =

13. 13
2-Class Cases:
• What is the entropy of a group in which all
examples belong to the same class?
– entropy = - 1 log21 = 0
• What is the entropy of a group with 50%
in either class?
– entropy = -0.5 log20.5 – 0.5 log20.5 =1
Minimum
impurity
Maximum
impurity

14. 14
Information Gain
Which test is more informative?
Split over whether
Balance exceeds 50K
Over 50KLess or equal 50K EmployedUnemployed
Split over whether
applicant is employed

15. 15
Impurity/Entropy (informal)
– Measures the level of impurity in a group of examples
Information Gain
Less impure Minimum
impurity
Very impure group
Gain aims to answer “how much
entropy of the training set some test
reduced ??”

16. 16
Information Gain
• We want to determine which attribute in a given set
of training feature vectors is most useful for
discriminating between the classes to be learned.
• Information gain tells us how important a given
attribute of the feature vectors is.
• We will use it to decide the ordering of attributes in
the nodes of a decision tree.

17. 17
Calculating Information Gain
996.0
30
16
log
30
16
30
14
log
30
14
22 











mpurity
787.0
17
4
log
17
4
17
13
log
17
13
22 











impurity
Entire population (30 instances)
17 instances
13 instances
(Weighted) Average Entropy of Children = 615.0391.0
30
13
787.0
30
17













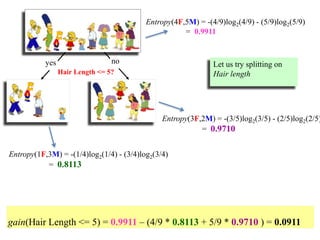
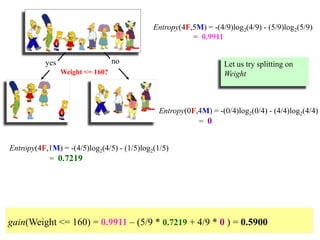
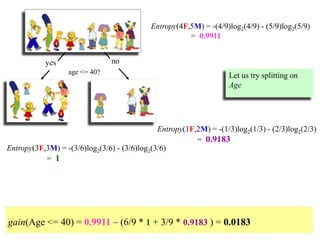
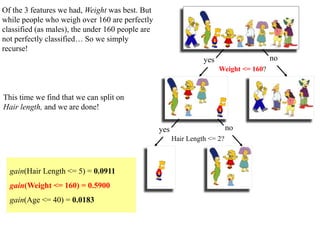
Information Gain= 0.996 - 0.615 = 0.38
391.0
13
12
log
13
12
13
1
log
13
1
22 











impurity
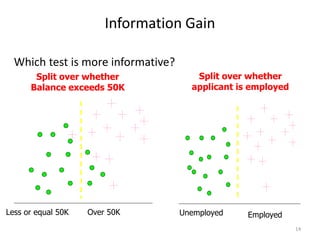
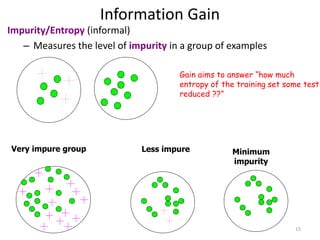
Information Gain = entropy(parent) – [average entropy(children)]
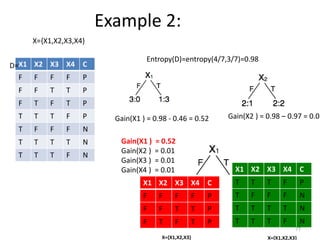
gain(population)=info([14,16])-info([13,4],[1,12])
parent
entropy
child
entropy
child
entropy

18. 18
Calculating Information Gain
615.0391.0
30
13
787.0
30
17













Information Gain= info([14,16])-info([13,4],[1,12])
= 0.996 - 0.615
= 0.38
391.0
13
12
log
13
12
13
1
log
13
1
22 











impurity
Information Gain = entropy(parent) – [average entropy(children)]
gain(population)=info([14,16])-info([13,4],[1,12])
info[14/16]=entropy(14/30,16/30) =
info[13,4]=entropy(13/17,4/17) =
info[1.12]=entropy(1/13,12/13) =
996.0
30
16
log
30
16
30
14
log
30
14
22 











impurity
787.0
17
4
log
17
4
17
13
log
17
13
22 











impurity
info([13,4],[1,12]) =

19. Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Overcast Hot High False Yes
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Overcast Cool Normal True Yes
Sunny Mild High False No
Sunny Cool Normal False Yes
Rainy Mild Normal False Yes
Sunny Mild Normal True Yes
Overcast Mild High True Yes
Overcast Hot Normal False Yes
Rainy Mild High True No
Which attribute to select?

21. Outlook = Sunny :
info[([2,3])=
Outlook = Overcast :
Info([4,0])=
Outlook = Rainy :
Info([2,3])=

i
ii pp 2log

22. Outlook = Sunny :
info[([2,3])=entropy(2/5,3/5)=
Outlook = Overcast :
Info([4,0])=entropy(1,0)=
Outlook = Rainy :
Info([2,3])=entropy(3/5,2/5)=

i
ii pp 2log

23. Outlook = Sunny :
info[([2,3])=entropy(2/5,3/5)=−2/5log(2/5)−3/5log(3/5)=0.971bits
Outlook = Overcast :
Info([4,0])=entropy(1,0)=−1log(1)−0log(0)=0bits
Outlook = Rainy :
Info([2,3])=entropy(3/5,2/5)=−3/5log(3/5)−2/5log(2/5)=0.971bits
Expected information for attribute:
Info([3,2],[4,0],[3,2])=
Note: log(0) is normally
undefined but we
evaluate 0*log(0) as
zero
(Weighted) Average Entropy of Children =

i
ii pp 2log

24. Outlook = Sunny :
info[([2,3])=entropy(2/5,3/5)=−2/5log(2/5)−3/5log(3/5)=0.971bits
Outlook = Overcast :
Info([4,0])=entropy(1,0)=−1log(1)−0log(0)=0bits
Outlook = Rainy :
Info([2,3])=entropy(3/5,2/5)=−3/5log(3/5)−2/5log(2/5)=0.971bits
Expected information for attribute:
Info([3,2],[4,0],[3,2])=(5/14)×0.971+(4/14)×0+(5/14)×0.971=0.693bits
Information gain= information before splitting – information after splitting
gain(Outlook ) = info([9,5]) – info([2,3],[4,0],[3,2])
Note: log(0) is normally
undefined but we
evaluate 0*log(0) as
zero

i
ii pp 2log

25. Outlook = Sunny :
info[([2,3])=entropy(2/5,3/5)=−2/5log(2/5)−3/5log(3/5)=0.971bits
Outlook = Overcast :
Info([4,0])=entropy(1,0)=−1log(1)−0log(0)=0bits
Outlook = Rainy :
Info([2,3])=entropy(3/5,2/5)=−3/5log(3/5)−2/5log(2/5)=0.971bits
Expected information for attribute:
Info([3,2],[4,0],[3,2])=(5/14)×0.971+(4/14)×0+(5/14)×0.971=0.693bits
Information gain= information before splitting – information after splitting
gain(Outlook ) = info([9,5]) – info([2,3],[4,0],[3,2])
= 0.940 – 0.693
= 0.247 bits
Note: log(0) is normally
undefined but we
evaluate 0*log(0) as
zero

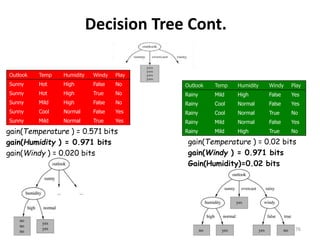
26. Humidity = high :
info[([3,4])=entropy(3/7,4/7)=−3/7log(3/7)−4/7log(4/7)=0.524+0.461=0.985 bits
Humidity = normal :
Info([6,1])=entropy(6/7,1/7)=−6/7log(6/7)−1/7log(1/7)=0.191+0.401=0.592 bits
Expected information for attribute:
Info([3,4],[6,1])=(7/14)×0.985+(7/14)×0.592=0.492+0.296= 0.788 bits
Information gain= information before splitting – information after splitting
gain(Humidity ) = info([9,5]) – info([3,4],[6,1])
= 0.940 – 0.788
= 0.152 bits

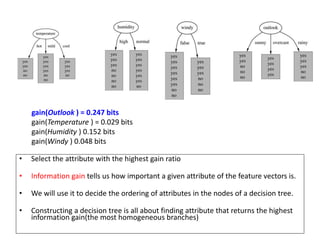
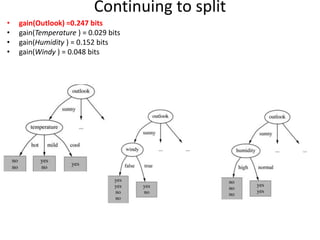
27. gain(Outlook ) = 0.247 bits
gain(Temperature ) = 0.029 bits
gain(Humidity ) 0.152 bits
gain(Windy ) 0.048 bits
info(nodes)
=Info([2,3],[4,0],[3,2])
=0.693bits
gain= 0.940-0.693
= 0.247 bits
info(nodes)
=Info([6,2],[3,3])
=0.892 bits
gain=0.940-0.892
= 0.048 bits
info(nodes)
=Info([2,2],[4,2],[3,1])
=0.911 bits
gain=0.940-0.911
= 0.029 bits
info(nodes)
=Info([3,4],[6,1])
=0.788bits
gain= 0.940-0.788
=0.152 bits
Info(all features) =Info(9,5) =0.940 bits
This nodes is “pure” with only
“yes” pattern, therefore lower
entropy and higher gain

28. gain(Outlook ) = 0.247 bits
gain(Temperature ) = 0.029 bits
gain(Humidity ) 0.152 bits
gain(Windy ) 0.048 bits
• Select the attribute with the highest gain ratio
• Information gain tells us how important a given attribute of the feature vectors is.
• We will use it to decide the ordering of attributes in the nodes of a decision tree.
• Constructing a decision tree is all about finding attribute that returns the highest
information gain(the most homogeneous branches)

29. Continuing to split
• gain(Outlook) =0.247 bits
• gain(Temperature ) = 0.029 bits
• gain(Humidity ) = 0.152 bits
• gain(Windy ) = 0.048 bits

30. Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Overcast Hot High False Yes
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Overcast Cool Normal True Yes
Sunny Mild High False No
Sunny Cool Normal False Yes
Rainy Mild Normal False Yes
Sunny Mild Normal True Yes
Overcast Mild High True Yes
Overcast Hot Normal False Yes
Rainy Mild High True No
Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Sunny Mild High False No
Sunny Cool Normal False Yes
Sunny Mild Normal True Yes
Temp Humidity Windy Play
Hot High False No
Hot High True No
Mild High False No
Cool Normal False Yes
Mild Normal True Yes

31. Temp Humidity Windy Play
Hot High False No
Hot High True No
Mild High False No
Cool Normal False Yes
Mild Normal True Yes
Temperature
No
No
Hot
Yes
No
Yes
Mild
Cool
Windy
No
No
Yes
False
No
Yes
True
Humidity
No
No
No
High
Yes
Yes
Normal
Play
No
No
No
Yes
Yes

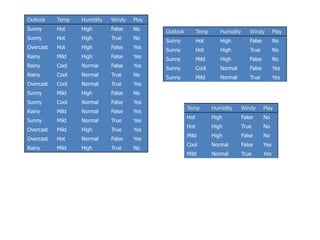
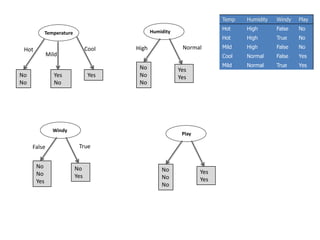
32. Temperature
No
No
Hot
Yes
No
Yes
Mild
Cool
Windy
No
No
Yes
False
No
Yes
True
Temperature = Hot :
info[([2,0])=entropy(1,0)=entropy(1,0)=−1log(1)−0log(0)=0 bits
Temperature = Mild :
Info([1,1])=entropy(1/2,1/2)=−1/2log(1/2)−1/2log(1/2)=0.5+0.5=1 bits
Temperature = Cool :
Info([1,0])=entropy(1,0)= 0 bits
Expected information for attribute:
Info([2,0],[1,1],[1,0])=(2/5)×0+(2/5)×1+(1/5)x0=0+0.4+0= 0.4 bits
gain(Temperature ) = info([3,2]) – info([2,0],[1,1],[1,0])
= 0.971-0.4= 0.571 bits
Play
No
No
No
Yes
Yes
Windy = False :
info[([2,1])=entropy(2/3,1/3)=−2/3log(2/3)−1/3log(1/3)=0.9179 bits
Windy = True :
Info([1,1])=entropy(1/2,1/2)=1 bits
Expected information for attribute:
Info([2,1],[1,1])=(3/5)×0.918+(2/5)×1=0.951bits
gain(Windy ) = info([3,2]) – info([2,1],[1,1])
= 0.971-0.951= 0.020 bits
Humidity
No
No
No
High
Yes
Yes
Normal
Humidity = High :
info[([3,0])=entropy(1,0)=0bits
Humidity = Normal :
Info([2,0])=entropy(1,0)=0 bits
Expected information for attribute:
Info([3,0],[2,0])=(3/5)×0+(2/5)×0=0 bits
gain(Humidity ) = info([3,2]) – Info([3,0],[2,0])
= 0.971-0= 0.971 bits
gain(Temperature ) = 0.571 bits
gain(Humidity ) = 0.971 bits
gain(Windy ) = 0.020 bits

33. Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Overcast Hot High False Yes
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Overcast Cool Normal True Yes
Sunny Mild High False No
Sunny Cool Normal False Yes
Rainy Mild Normal False Yes
Sunny Mild Normal True Yes
Overcast Mild High True Yes
Overcast Hot Normal False Yes
Rainy Mild High True No
Outlook Temp Humidity Windy Play
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Rainy Mild Normal False Yes
Rainy Mild High True No
Temp Humidity Windy Play
Mild High False Yes
Cool Normal False Yes
Cool Normal True No
Mild Normal False Yes
Mild High True No
Temp Windy Play
Mild False Yes
Cool False Yes
Cool True No
Mild False Yes
Mild True No

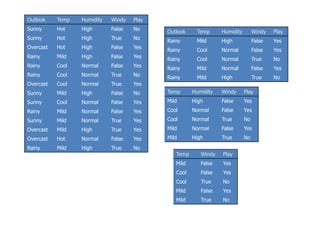
34. Temp Windy Play
Mild False Yes
Cool False Yes
Cool True No
Mild False Yes
Mild True No
Temperature
---
Hot
Yes
Yes
No
Yes
No
Mild
Cool
Windy
Yes
Yes
Yes
False
No
No
True
Temperature = Mild :
Info([2,1])=entropy(1/2,1/2)=0.9179 bits
Temperature = Cool :
Info([1,1])=1 bits
Expected information for attribute:
Info([2,1],[1,1])=(3/5)×0.918+(2/5)×1=0.551+0.4= 0.951 bits
gain(Temperature ) = info([3,2]) – info([2,1],[1,1])
= 0.971-0.951= 0.02 bits
Play
Yes
Yes
Yes
No
No
Windy = False :
info[([3,0])=0 bits
Windy = True :
Info([2,0])=0 bits
Expected information for attribute:
Info([3,0],[2,0])= 0 bits
gain(Windy ) = info([3,2]) – info([3,0],[2,0])
= 0.971-0= 0.971 bits
gain(Temperature ) = 0.02 bits
gain(Windy ) = 0.971 bits

35. Final decision tree
R1: If (Outlook=Sunny) And (Humidity=High) then Play=No
R2: If (Outlook=Sunny) And (Humidity=Normal) then Play=Yes
R3: If (Outlook=Overcast) then Play=Yes
R4: If (Outlook=Rainy) And (Windy=False) then Play=Yes
R5: If (Outlook=Rainy) And (Windy=True) then Play=No
Note: not all leaves need to be pure; sometimes identical
instances have different classes
⇒ Splitting stops when data can’t be split any further
When the set contains
only samples belonging
to a single pattern, the
decision tree is
composed by a leaf

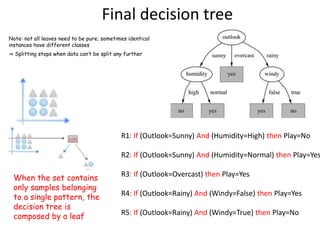
36. Wishlist for a purity measure
• Properties we require from a purity measure:
– When node is pure, measure should be zero
– When impurity is maximal (i.e. all classes equally likely),
measure should be maximal
– Measure should obey multistage property (i.e. decisions
can be made in several stages)
Measure ([ 2,3,4 ])=measure ([ 2,7 ]+(7 / 9)×measure
([ 3,4 ])
• Entropy is the only function that satisfies all three
properties!

37. Properties of the entropy
• The multistage property:
• Simplification of computation:
•

38. Highly-branching attributes
• Problematic: attributes with a large number of
values (extreme case: ID code)
• Subsets are more likely to be pure if there is a
large number of values
– Information gain is biased towards choosing
attributes with a large number of values
– This may result in overfitting (selection of an
attribute that is non-optimal for prediction)
• Another problem: fragmentation

39. Information gain is maximal for ID code (namely 0.940 bits)
Entropy of split:

40. Gain Ratio
• Gain ratio: a modification of the information gain
that reduces its bias
• Gain ratio takes number and size of branches into
account when choosing an attribute
– It corrects the information gain by taking the intrinsic
information of a split into account
• Intrinsic information: entropy of distribution of
instances into branches (i.e. how much info do
we need to tell which branch an instance belongs
to)

41. Computing the gain ratio
• Example: intrinsic information for ID code
– Info([1,1,...,1])=14×(−1/14×log(1/14))=3.807bits
• Value of attribute decreases as intrinsic
information gets larger
• Definition of gain ratio:
gain_ratio(attribute)=gain(attribute)
intrinsic_info(attribute)
• Example:
gain_ratio(ID code)=0.940 bits =0.246
3.807 bits

42. Gain ratios for weather data

43. • Assume attributes are discrete
– Discretize continues attributes
• Choose the attribute with the highest Information
gain
• Create branches for each value of attribute
• Examples partitioned based on selected attributes
• Repeat with remaining attributes
• Stropping conditions
– All examples assigned the same label
– No examples left
Building a Decision Tree(ID3 algorithm)

44. C4.5 Extensions
Consider every possible binary
partition: choose the partition with the
highest gain

45. • Top-down induction of decision trees: ID3,
algorithm developed by Ross Quinlan
– Gain ratio just one modification of this basic algorithm
– ⇒ C4.5: deals with numeric attributes, missing values,
noisy data
• Similar approach: CART
• There are many other attribute selection criteria!
(But little difference in accuracy of result)
Discussion

46. Q
• Suppose there is a student that decides whether or not to go in to campus
on any given day based on the weather, wakeup time, and whether there
is a seminar talk he is interested in attending. There are data collected
from 13 days.

47. Person Hair
Length
Weight Age Class
Homer 0” 250 36 M
Marge 10” 150 34 F
Bart 2” 90 10 M
Lisa 6” 78 8 F
Maggie 4” 20 1 F
Abe 1” 170 70 M
Selma 8” 160 41 F
Otto 10” 180 38 M
Krusty 6” 200 45 M
Comic 8” 290 38 ?

48. Person Hair
Length
Weight Age Class
Homer 0” 250 36 M
Marge 10” 150 34 F
Bart 2” 90 10 M
Lisa 6” 78 8 F
Maggie 4” 20 1 F
Abe 1” 170 70 M
Selma 8” 160 41 F
Otto 10” 180 38 M
Krusty 6” 200 45 M
Comic 8” 290 38 ?

49. Hair Length <= 5?
yes no
Entropy(4F,5M) = -(4/9)log2(4/9) - (5/9)log2(5/9)
= 0.9911
Entropy(1F,3M) = -(1/4)log2(1/4) - (3/4)log2(3/4)
= 0.8113
Entropy(3F,2M) = -(3/5)log2(3/5) - (2/5)log2(2/5)
= 0.9710
gain(Hair Length <= 5) = 0.9911 – (4/9 * 0.8113 + 5/9 * 0.9710 ) = 0.0911
Let us try splitting on
Hair length

50. Weight <= 160?
yes no
Entropy(4F,5M) = -(4/9)log2(4/9) - (5/9)log2(5/9)
= 0.9911
Entropy(4F,1M) = -(4/5)log2(4/5) - (1/5)log2(1/5)
= 0.7219
Entropy(0F,4M) = -(0/4)log2(0/4) - (4/4)log2(4/4)
= 0
gain(Weight <= 160) = 0.9911 – (5/9 * 0.7219 + 4/9 * 0 ) = 0.5900
Let us try splitting on
Weight

51. age <= 40?
yes no
Entropy(4F,5M) = -(4/9)log2(4/9) - (5/9)log2(5/9)
= 0.9911
Entropy(3F,3M) = -(3/6)log2(3/6) - (3/6)log2(3/6)
= 1
Entropy(1F,2M) = -(1/3)log2(1/3) - (2/3)log2(2/3)
= 0.9183
gain(Age <= 40) = 0.9911 – (6/9 * 1 + 3/9 * 0.9183 ) = 0.0183
Let us try splitting on
Age

52. Weight <= 160?
yes no
Hair Length <= 2?
yes no
Of the 3 features we had, Weight was best. But
while people who weigh over 160 are perfectly
classified (as males), the under 160 people are
not perfectly classified… So we simply
recurse!
This time we find that we can split on
Hair length, and we are done!
gain(Hair Length <= 5) = 0.0911
gain(Weight <= 160) = 0.5900
gain(Age <= 40) = 0.0183

53. Person Hair
Length
Weight Age Class
Marge 10” 150 34 F
Bart 2” 90 10 M
Lisa 6” 78 8 F
Maggie 4” 20 1 F
Selma 8” 160 41 F

54. Hair Length <= 2?
Entropy(4F,1M) = -(4/5)log2(4/5) – (1/5)log2(1/5)
= 0.2575+0.464
= 0.721
yes no
Entropy(0F,1M) =0
Entropy(4F,0M) = 0
gain(Hair Length <= 2) = 0.721 -0= 0.721

55. Age <= 2?
Entropy(4F,1M) = -(4/5)log2(4/5) – (1/5)log2(1/5)
= 0.2575+0.464
= 0.721
yes no
Entropy(0F,1M) =0
Entropy(4F,0M) = 0
gain(Hair Length <= 2) = 0.721 -0= 0.721
age <= 40?

56. Decision Tree
• Lunch with girlfriend
• Enter the restaurant or not?

57. • Input: features about restaurant
• Output: Enter or not
• Classification or Regression Problem?
• Classification
• Features/Attributes:
– Type: Italian, French,Thai
– Environment: Fancy, classical
– Occupied?

58. Occupied Type Rainy Hungry Gf/friend Happiness Class
T Pizza T T T T
F Thai T T T F
T Thai F T T F
F Other F T T F
T Other F T T T

59. Example of C4.5 algorithm
TABLE 7.1 (p.145)
A simple flat database
of examples for training

60. • If I flip a coin N times and get A heads, what is
the probability of getting heads on toss N+1
A+2
N+2
Rule of Succession

61. • I have a weighted coin but I don’t know what
the likehoods are for flipping heads or tails
• I flip the coin 10 times, always get heads
• What’s the probability of getting heads on 11th
try?
– A+1/N+2=10+1/10+2=11/12

62. • What is the probability that the sun will rise
tomorrow?
• N=1.8 x10^12 days
• A=1.8x10^12 days
99.999999999944%

63. Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Sunny Mild High False No
Sunny Cool Normal False Yes
Sunny Mild Normal True Yes
Outlook Temp Humidity Windy Play
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Rainy Mild Normal False Yes
Rainy Mild High True No
gain(Temperature ) = 0.571 bits
gain(Humidity ) = 0.971 bits
gain(Windy ) = 0.020 bits
gain(Temperature ) = 0.02 bits
gain(Windy ) = 0.971 bits
Gain(Humidity)=0.02 bits

64. Example 3:

65. X1 X2 X3 X4 C
F F F F P
F F T T P
F T F T P
T T T F P
T F F F N
T T T T N
T T T F N
D=
X={X1,X2,X3,X4}
Entropy(D)=entropy(4/7,3/7)=0.98
Gain(X1 ) = 0.98 - 0.46 = 0.52
Gain(X2 ) = 0.98 – 0.97 = 0.01
Gain(X1 ) = 0.52
Gain(X2 ) = 0.01
Gain(X3 ) = 0.01
Gain(X4 ) = 0.01
X1 X2 X3 X4 C
F F F F P
F F T T P
F T F T P
X1 X2 X3 X4 C
T T T F P
T F F F N
T T T T N
T T T F N
X={X1,X2,X3}
X={X1,X2,X3}

66. X1 X2 X3 X4 C
F F F F P
F F T T P
F T F T P
X1 X2 X3 X4 C
T T T F P
T F F F N
T T T T N
T T T F N
X={X1,X2,X3}
All instances have the same class.
Return class P
All attributes have same information gain.
Break ties arbitrarily.
Choose X2
X1 X2 X3 X4 C
T F F F N
X1 X2 X3 X4 C
T T T F P
T T T T N
T T T F N
X={X1,X2,X3}
X={X3,X4}
All instances have the same class.
Return class N
X={X3,X4
X3 has zero information gain
X4 has positive information gain Choose X4

67. X1 X2 X3 X4 C
T T T T N
X1 X2 X3 X4 C
T T T F P
T T T F N
X={X3}
X3 has zero information gain
No suitable attribute for splitting
Return most common class (break ties
arbitrarily)
Note: data is inconsistent!
X={X3}
All instances have the same class. Return N.

68. Example 4

69. Outlook Temp Humidity Windy Play
Sunny Hot High False Yes
Sunny Hot High True No
Overcast Hot High False Yes
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Overcast Cool Normal True Yes
Sunny Mild High False No
Sunny Cool Normal False Yes
Rainy Mild Normal False Yes
Sunny Mild Normal True Yes
Overcast Mild High True Yes
Overcast Hot Normal False Yes
Rainy Mild High True No
Outlook
Humidity Windy
Temperature
Windy
No Yes
YesYes
No
No
RainySunny
Overcast
YesHigh
Normal
Hot
Mild
True False

70. Outlook Temp Humidity Windy Play
Sunny Hot High False Yes
Sunny Hot High True No
Sunny Mild High False No
Sunny Cool Normal False Yes
Sunny Mild Normal True Yes
Outlook
Humidity Windy
YesYes No
RainySunny
Overcast
YesHigh
Normal
Gain(Temperature)=0.971-0.8=0.171
Gain(Windy)=0.971-0.951=0.020
Gain(Humidity)=0.971-0.551=0.420
O T H W P
S H H F Y
S H H T N
S M H F N
O T H W P
S C N F Y
S M N T Y

71. Humidity Windy
Temperature YesYes No
RainySunny
Overcast
YesHigh
Normal
Hot
Mild
Outlook
O T H W P
S H H F Y
S H H T N
S M H F N
Temperature
Yes
No
Hot
No
Mild
Windy
No
Yes
False
No
True
O T H W P
S H H F Y
S H H T N
O T H W P
S M H F N

72. Outlook
Humidity Windy
Temperature
Windy
No Yes
Yes
No
No
RainySunny
Overcast
YesHigh
Normal
Hot
Mild
True FalseO T H W P
S H H T N O T H W P
S H H F Y
Yes

73. Outlook Temp Humidity Windy Play
Sunny Hot High False No
Sunny Hot High True No
Sunny Mild High False No
Sunny Cool Normal False Yes
Sunny Mild Normal True Yes
Outlook Temp Humidity Windy Play
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Rainy Mild Normal False Yes
Rainy Mild High True Nogain(Temperature ) = 0.571 bits
gain(Humidity ) = 0.971 bits
gain(Windy ) = 0.020 bits
gain(Temperature ) = 0.02 bits
gain(Windy ) = 0.971 bits
Gain(Humidity)=0.02 bits
Decision Tree Cont.
76

74. X1 X2 X3 X4 C
F F F F P
F F T T P
F T F T P
T T T F P
T F F F N
T T T T N
T T T F N
D=
X={X1,X2,X3,X4}
Entropy(D)=entropy(4/7,3/7)=0.98
Gain(X1 ) = 0.98 - 0.46 = 0.52 Gain(X2 ) = 0.98 – 0.97 = 0.01
Gain(X1 ) = 0.52
Gain(X2 ) = 0.01
Gain(X3 ) = 0.01
Gain(X4 ) = 0.01
X1 X2 X3 X4 C
F F F F P
F F T T P
F T F T P
X1 X2 X3 X4 C
T T T F P
T F F F N
T T T T N
T T T F N
X={X1,X2,X3} X={X1,X2,X3}
Example 2:
77

75. X1 X2 X3 X4 C
F F F F P
F F T T P
F T F T P
X1 X2 X3 X4 C
T T T F P
T F F F N
T T T T N
T T T F N
X={X1,X2,X3}
All instances have the same class.
Return class P
All attributes have same information gain.
Break ties arbitrarily.
Choose X2
X1 X2 X3 X4 C
T F F F N
X1 X2 X3 X4 C
T T T F P
T T T T N
T T T F N
X={X1,X2,X3}
X={X3,X4}
All instances have the same class.
Return class N
X={X3,X4
X3 has zero information gain
X4 has positive information gain Choose X4
78

76. X1 X2 X3 X4 C
T T T T N
X1 X2 X3 X4 C
T T T F P
T T T F N
X={X3}
X3 has zero information gain
No suitable attribute for splitting
Return most common class (break ties
arbitrarily)
Note: data is inconsistent!
X={X3}
All instances have the same class. Return N.
79

77. Outlook Temp Humidity Windy Play
Sunny Hot High False Yes
Sunny Hot High True No
Overcast Hot High False Yes
Rainy Mild High False Yes
Rainy Cool Normal False Yes
Rainy Cool Normal True No
Overcast Cool Normal True Yes
Sunny Mild High False No
Sunny Cool Normal False Yes
Rainy Mild Normal False Yes
Sunny Mild Normal True Yes
Overcast Mild High True Yes
Overcast Hot Normal False Yes
Rainy Mild High True No
Outlook
Humidity Windy
Temperature
Windy
No Yes
Yes
Yes
No
No
RainySunny
Overcast
YesHigh
Normal
Hot
Mild
True False
Example 3
80

78. Outlook Temp Humidity Windy Play
Sunny Hot High False Yes
Sunny Hot High True No
Sunny Mild High False No
Sunny Cool Normal False Yes
Sunny Mild Normal True Yes
Outlook
Humidity Windy
YesYes No
RainySunny
Overcast
YesHigh
Normal
Gain(Temperature)=0.971-0.8=0.171
Gain(Windy)=0.971-0.951=0.020
Gain(Humidity)=0.971-0.551=0.420
O T H W P
S H H F Y
S H H T N
S M H F N
O T H W P
S C N F Y
S M N T Y
81

79. Humidity Windy
Temperature YesYes No
RainySunny
Overcast
YesHigh
Normal
Hot
Mild
Outlook
O T H W P
S H H F Y
S H H T N
S M H F N
Temperature
Yes
No
Hot
No
Mild
Windy
No
Yes
False
No
True
O T H W P
S H H F Y
S H H T N
O T H W P
S M H F N
82

80. Outlook
Humidity Windy
Temperature
Windy
No Yes
Yes
No
No
RainySunny
Overcast
YesHigh
Normal
Hot
Mild
True FalseO T H W P
S H H T N O T H W P
S H H F Y
Yes
83