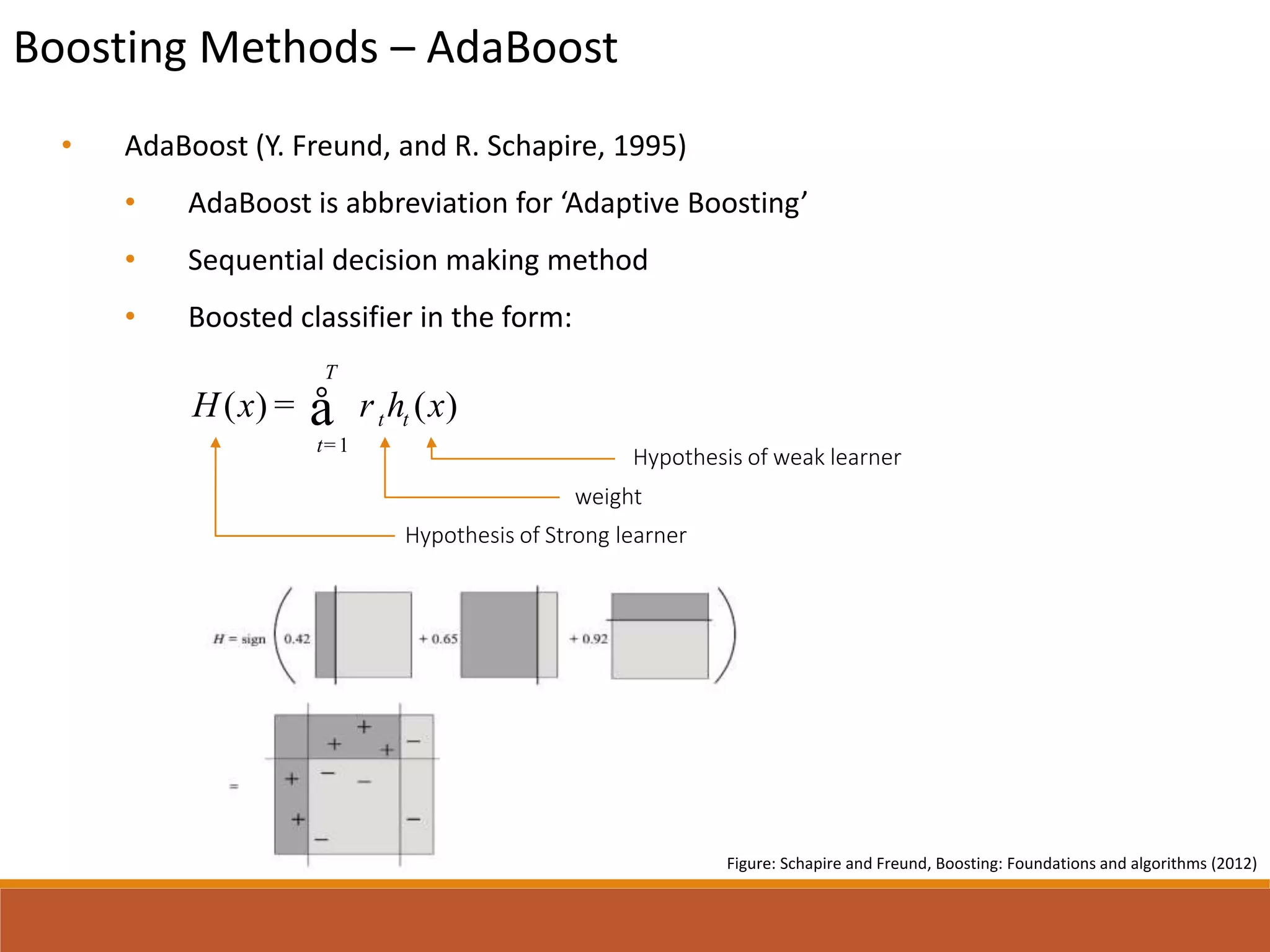
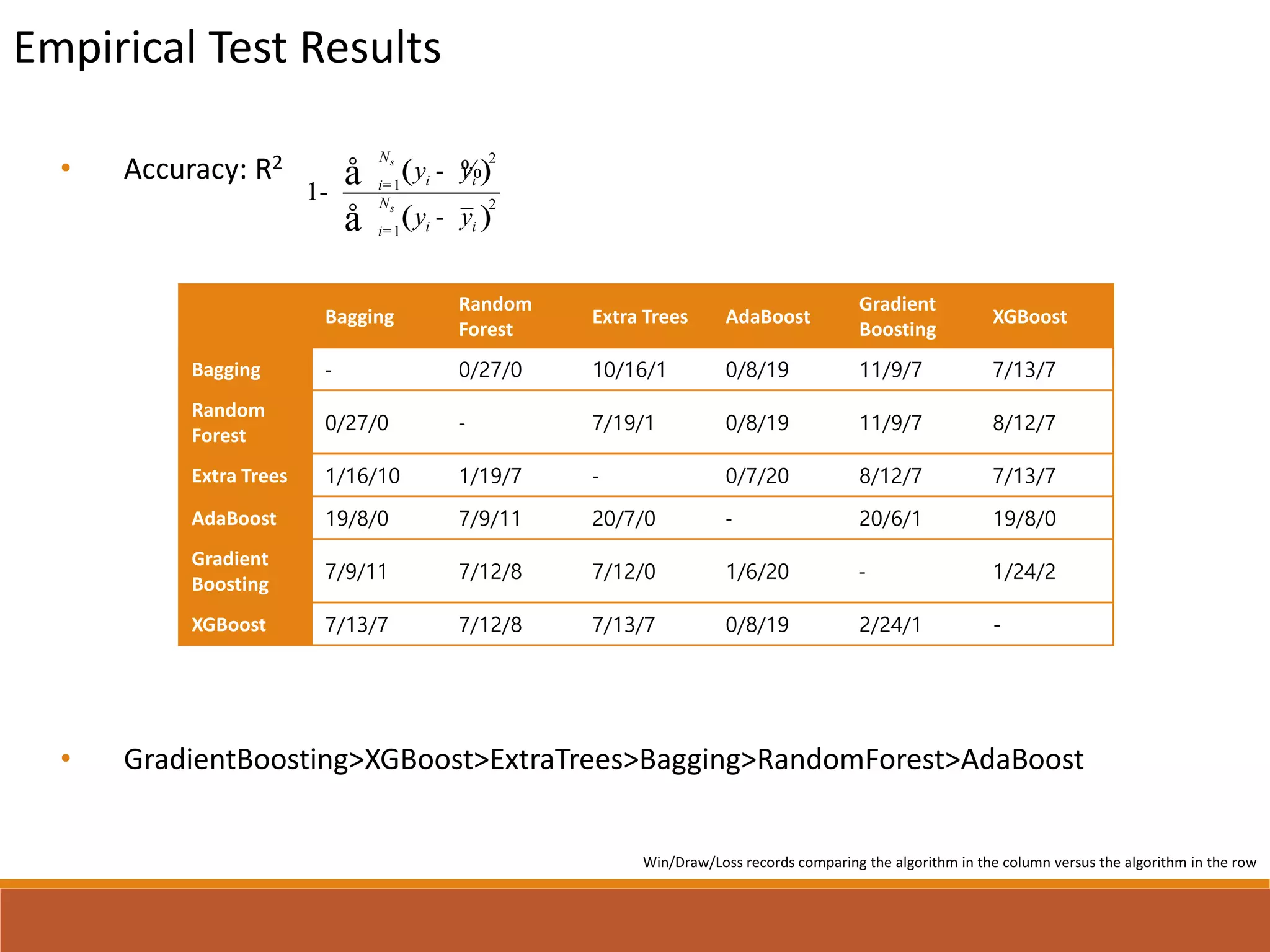
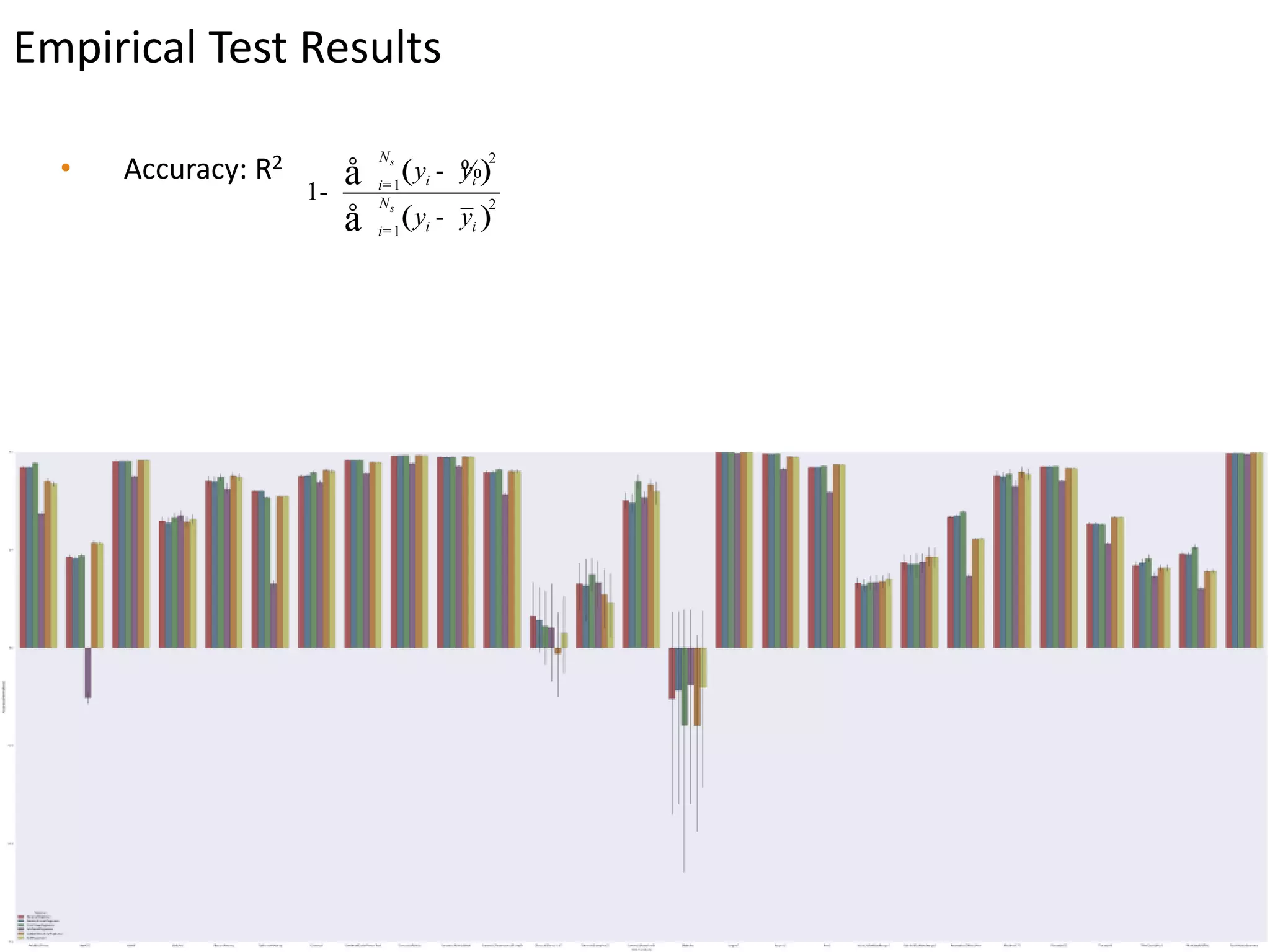
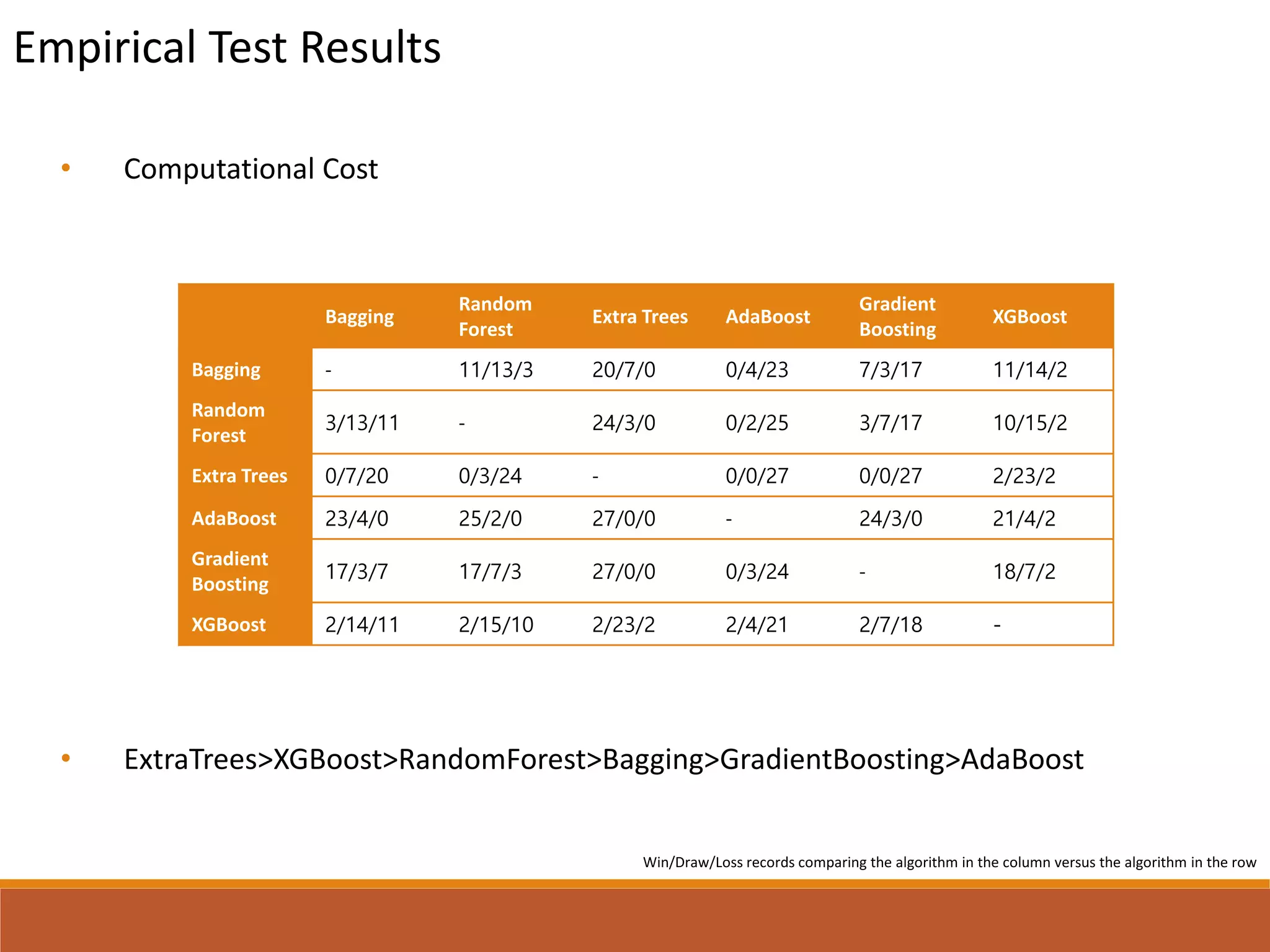
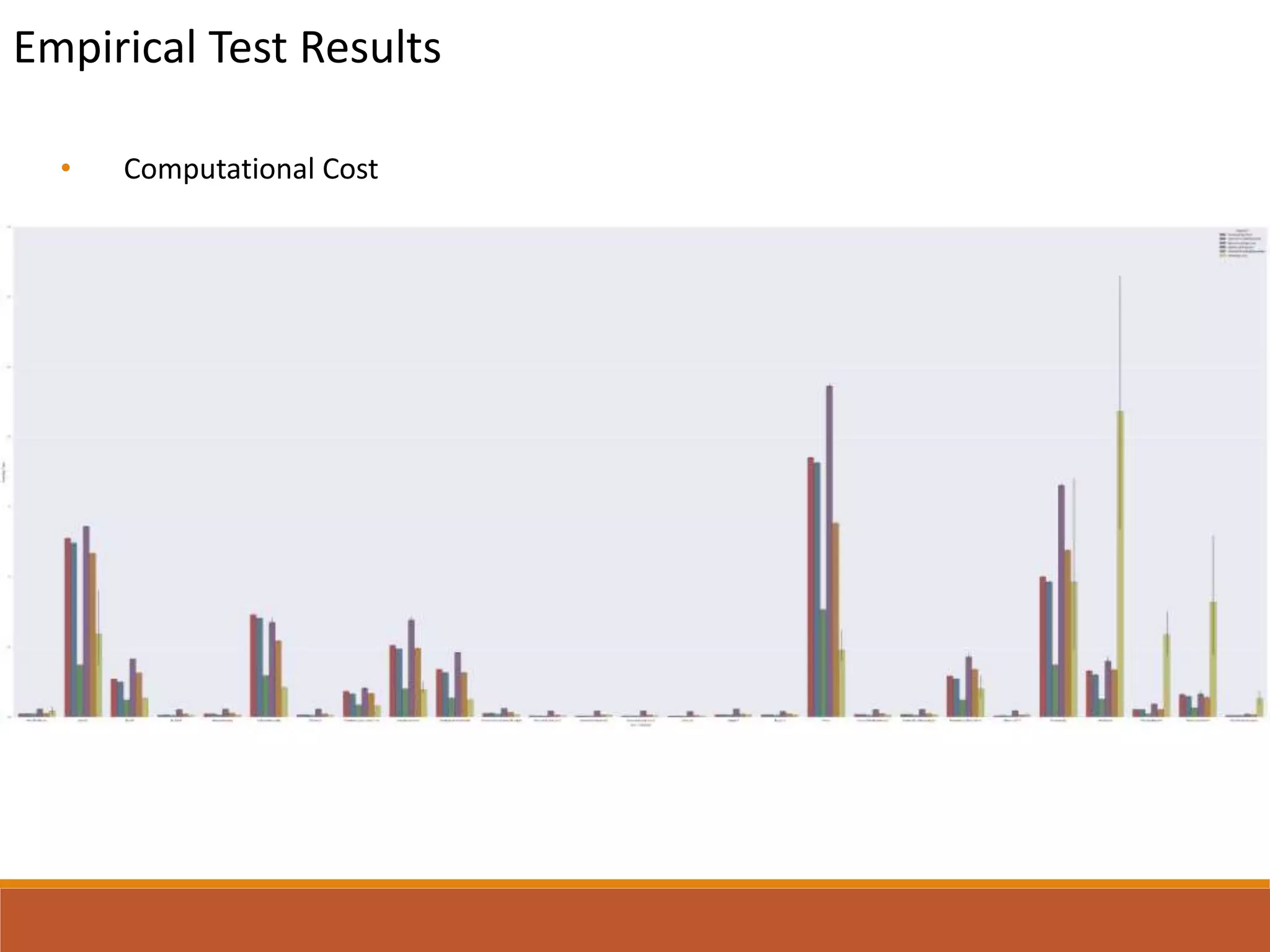
This document presents a comparative study of various decision tree ensembles for regression, focusing on their performance and time efficiency. Multiple algorithms such as bagging, boosting, and various tree-based methods are evaluated, with empirical test results indicating that gradient boosting and XGBoost generally outperform other methods. The study highlights the advantages and disadvantages of different ensemble methods, as well as the computational costs associated with each approach.

1. Comparison Study
of Decision Tree Ensembles
for Regression
SEONHO PARK

2. Objectives
• Empirical study of Ensemble trees for regression problems
• To verify its performance and time efficiency
• Candidates from open source
• Scikit-Learn
• BaggingRegressor
• RandomForestRegressor
• ExtraTreesRegressor
• AdaBoostRegressor
• GradientBoostingRegressor
• XGBoost
• XGBRegressor

3. Decision Tree
1x
2x2 2.5?x >
1 3.0?x >
N Y
N Y
• Expressed as a recursive partition of the feature space
• Use for both classifier and regressor
• Building blocks: nodes, leaves
• Node splits the instance space into two or more sub-spaces according to a certain
discrete function of the input feature values
2.5
3.0

4. Decision Tree Inducers
• How to generate decision tree?
• Rule to determine the decision tree is how to split and prune nodes
• Decision trees inducers:
ID3(Quinlan, 1986), C4.5(Quinlan, 1993), CART(Breiman et al., 1984)
• CART is most generable and popular

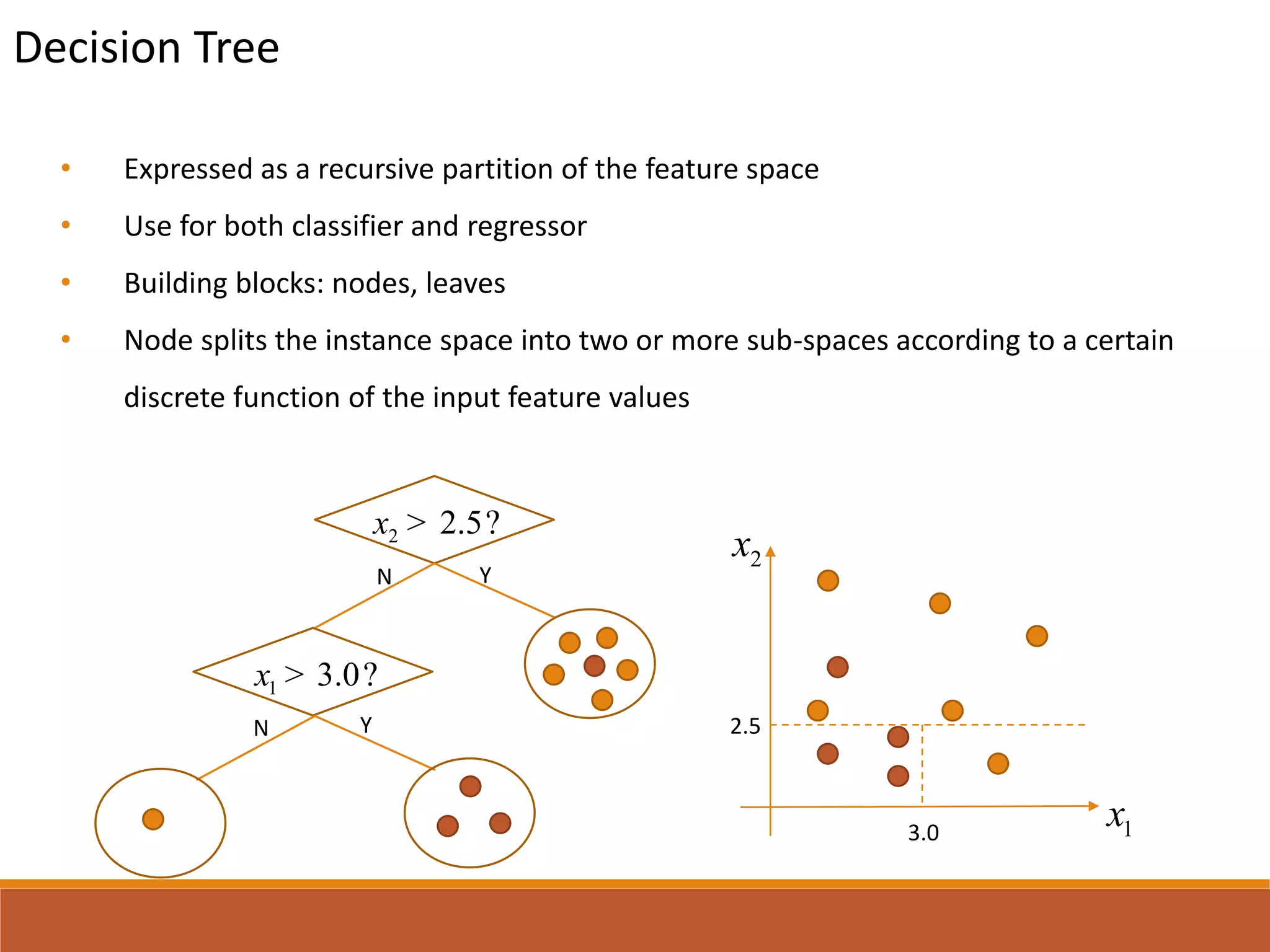
5. CART
• CART stands for Classification and Regression Trees
• Has ability to generate regression trees
• Minimization of misclassification costs
• In regression, the costs are represented for least squares between target values and
expected values
• Maximization of change of impurity function:
• For regression,
argmax ( ) ( ( )) ( ( ))
j
R
j p l l r r
x
x i t P i t P i té ù= - -ê úë û
[ ]arg min Var( ) Var( )
j
R
j l r
x
x Y Y= +

6. CART
• Pruning
• minimum number of points
Figure: Roman Timofeev, Classification and Regression Trees Theory and Applications, (2004)
minN

7. Decision Tree Pros And Cons
• Advantages
• Explicability: Easy to understand and interpret(white boxes)
• Make minimal assumptions
• Requires little data preparation
• Addressing nonlinearity in an intuitive manner
• Can handle both nominal and numerical features
• Perform well with large datasets
• Disadvantages
• Heuristics such as the greedy algorithm  local optimal decision at each node
• Instability, Overfitting – not to be robust to noise(outlier)

8. Ensemble Methods
• Tactics of Ensemble Tree can be classified by two types : Bagging and Boosting
• Bagging Methods: Tree Bagging, Random Forest, Extra Trees
• Boosting Methods: AdaBoost, Gradient Boosting
Figure: http://scikit-learn.org/stable/auto_examples/ensemble/plot_forest_iris.html

9. Averaging Methods
• Random Forest (L. Breiman, 2001)
• Tree Bagging + Split among a random subset of the feature
• Extra Trees (Extremely Randomized Trees) (P. Geurts et al., 2006)
• Random Forest + Extra Tree
• Extra Tree: thresholds at nodes are drawn at random
• Tree Bagging (L. Breiman, 1996)
• What is Bagging?
• BAGGING is abbreviation for Bootstrap AGGregatING
• Boosting: samples are drawn with replacement
• Drawn as random subsets of the features  ‘Random Subspace’(1999)
• Drawn as random subsets of both samples and features  ‘Random Patches’ (2012)

10. Boosting Methods – AdaBoost
• AdaBoost (Y. Freund, and R. Schapire, 1995)
• AdaBoost is abbreviation for ‘Adaptive Boosting’
• Sequential decision making method
• Boosted classifier in the form:
Hypothesis of weak learner
weight
Hypothesis of Strong learner
Figure: Schapire and Freund, Boosting: Foundations and algorithms (2012)
1
( ) ( )
T
t t
t
H x h xr
=
= å

11. Boosting Methods – AdaBoost

• Supposed that you are given (x1,y1),(x2,y2),…,(xn,yn), and the task is to fit model H(x).
And your friend wants to help you and gives you a model H. you check his model and
find it is good but not perfect. There are some mistakes: H(x1) = 0.8, H(x2) = 1.4…,
while y1= 0.9, y2=1.3… How can you improve this model?
• Rule
• Use friend model H without any modification of it
• Can add additional model h to improve prediction, so the new prediction will be
H+h
1
( ) ( )
T
t t
t
H x h xr
=
= å 1( ) ( )T T T TH x H h xr-= +

12. Boosting Methods – AdaBoost
1 1 1
2 2 2
( ) ( )
( ) ( )
...
( ) ( )n n n
H x h x y
H x h x y
H x h x y
+ =
+ =
+ =
• Wish to improve the model such that:

1 1 1
2 2 2
1
( ) ( )
( ) ( )
...
( ) ( )n n
h x y H x
h x y H x
h x y H x
= -
= -
= -
• Fit a weak learner h to data
(x1,y1-H(x1)),(x2,y2-H(x2)),…,(xn,yn-H(xn))
residual

13. Boosting Methods – Gradient Boosting
• AdaBoost: updates with loss function residual which will be converged to 0
• In scikit-learn, AdaBoost.R2 algorithm is implemented
• Gradient Boosting (L. Breiman, 1997)
: updates with negative gradients of loss functions which will be converged to 0
0y H- =
0
L
H
¶
- =
¶
*Drucker,H., Improving Regressors using Boosting Techniques (1997)

14. Boosting Methods – Gradient Boosting
• Loss function
• First order optimality
• If loss function is as follows:
• Negative gradients can be interpret as residuals
( , )L y H
( , )
0, 1,i i
i
L y H
i n
H
¶
= " =
¶
2
2
1
( , )
2
L y H y H= -
( , )
, 1,i i
i i
i
L y H
y H i n
H
¶
= - " =
¶

15. Boosting Methods – Gradient Boosting
• Square loss function is not adequate to treat the outliers  overfitting
• Other loss functions
• Absolute loss
• Huber loss
( , )L y H y H= -
( )
21
( ) if ,
2( , )
/ 2 otherwise
y H y H
L y H
y H
d
d d
ìïï - - £ïï= í
ïï - -ïïî

16. • Among the 29 kaggle challenge winning solutions during 2015,
• 17 used XGBoost (Gradient Boosting Trees)
(8 solely used XGBoost, 9 used XGBoost + deep neural nets)
• 11 used deep neural nets
(2 solely used, 9 combined with XGBoost)
• In KDDCup 2015, Ensemble Trees was used in every winning team in the top 10
XGBoost
*Tianqi Chen, XGBoost: A Scalable Tree Boosting System (2016)

17. Ensemble Method Pros and Cons
• Advantages
• Avoid overfitting
• Fast and scalable  handle large-scale data
• Almost work ‘out-of-the-box’
• Disadvantages
• Overfitting
• ad hoc heuristic
• Not provide probabilistic framework (confidence intervals, posterior
distributions)

18. Empirical Test Suits
• Diabetes1)
• Concrete Slump Test2)
• Machine CPU1)
• Body Fat3)
• Yacht Hydrodynamics2)
• Chemical4)
• Boston Housing5)
• Istanbul stock exchange2)
• Concrete compressive strength2)
• Engine4)
• Airfoil Self-Noise2)
• Wine Quality (Red) 2)
• Pumadyn (32) 1)
• Pumadyn (8) 1)
• Bank (8) 1)
• Bank (32) 1)
• Wine Quality (White) 2)
• Computer Activity6)
• Computer Activity_small6)
• Kinematics of Robot Arm1)
• Combined Cycle Power Plant2)
• California Housing7)
• Friedman8)
1)http://www.dcc.fc.up.pt/~ltorgo/
2)https://archive.ics.uci.edu/ml/datasets/
3)http://www.people.vcu.edu/~rjohnson/bios546/programs/
4)MATLAB neural fitting toolbox
5)https://rpubs.com/yroy/Boston
6)http://www.cs.toronto.edu/~delve/
7)5)http://www.cs.cmu.edu/afs/cs/academic/class/15381-s07/www/hw6/cal_housing.arff
8)http://tunedit.org/repo/UCI/numeric/fried.arff

19. Description of Comparison Methods
• Corrected t-test*
where , and denote the difference
• Data set is divided into a learning sample of a given size and a test sample of
size
• Assumed to follow a student distribution with d.o.f.
• We used confidential interval to 95% (type 1 error) to verify the hypothesis
• In this task, we repeated 30 times independently ( is 30)
• Parameters used for ensemble trees are as defaults
*Nadeau, C., Bengio, Y., Inference for the generalization error (2003)
i
d
i i
A Be e-
Tn
Ln
sN
21
( )
d
corr
T
d
s L
t
n
N n
m
s
=
+
1
sN
ii
d
s
d
N
m =
=
å
2
2 1
( )
1
sN
i di
d
s
d
N
m
s =
-
=
-
å
1sN -

20. • Accuracy: R2
• GradientBoosting>XGBoost>ExtraTrees>Bagging>RandomForest>AdaBoost
Win/Draw/Loss records comparing the algorithm in the column versus the algorithm in the row
Bagging
Random
Forest
Extra Trees AdaBoost
Gradient
Boosting
XGBoost
Bagging - 0/27/0 10/16/1 0/8/19 11/9/7 7/13/7
Random
Forest
0/27/0 - 7/19/1 0/8/19 11/9/7 8/12/7
Extra Trees 1/16/10 1/19/7 - 0/7/20 8/12/7 7/13/7
AdaBoost 19/8/0 7/9/11 20/7/0 - 20/6/1 19/8/0
Gradient
Boosting
7/9/11 7/12/8 7/12/0 1/6/20 - 1/24/2
XGBoost 7/13/7 7/12/8 7/13/7 0/8/19 2/24/1 -
Empirical Test Results
( )
( )
2
1
2
1
1
s
s
N
i ii
N
i ii
y y
y y
=
=
-
-
-
å
å
%

21. Empirical Test Results
• Accuracy: R2 ( )
( )
2
1
2
1
1
s
s
N
i ii
N
i ii
y y
y y
=
=
-
-
-
å
å
%

22. • Computational Cost
• ExtraTrees>XGBoost>RandomForest>Bagging>GradientBoosting>AdaBoost
Bagging
Random
Forest
Extra Trees AdaBoost
Gradient
Boosting
XGBoost
Bagging - 11/13/3 20/7/0 0/4/23 7/3/17 11/14/2
Random
Forest
3/13/11 - 24/3/0 0/2/25 3/7/17 10/15/2
Extra Trees 0/7/20 0/3/24 - 0/0/27 0/0/27 2/23/2
AdaBoost 23/4/0 25/2/0 27/0/0 - 24/3/0 21/4/2
Gradient
Boosting
17/3/7 17/7/3 27/0/0 0/3/24 - 18/7/2
XGBoost 2/14/11 2/15/10 2/23/2 2/4/21 2/7/18 -
Empirical Test Results
Win/Draw/Loss records comparing the algorithm in the column versus the algorithm in the row

23. Empirical Test Results
• Computational Cost