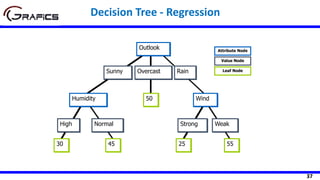
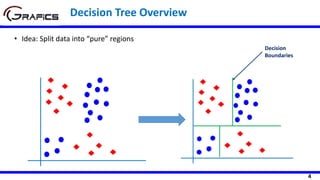
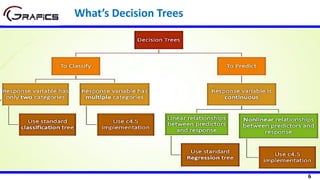
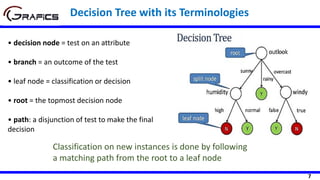
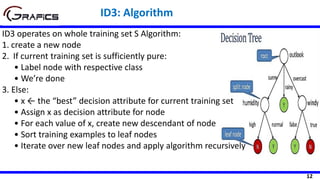
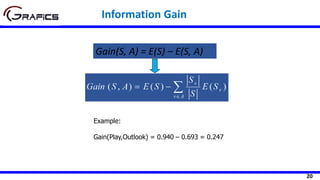
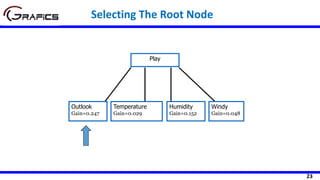
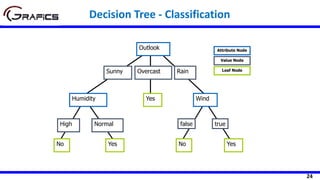
The document discusses decision tree models in machine learning. It begins by defining key terms like decision nodes, branches, and leaf nodes. It then explains how decision trees are built in a top-down manner by recursively splitting the training data based on selected attributes. The document also covers different algorithms for building decision trees like ID3, C4.5, and CART. It discusses measures used for attribute selection like information gain, gain ratio, and Gini index. Finally, it provides an example of how to build a decision tree to classify whether to play tennis based on weather attributes.

1. Mathematics behind
Machine Learning:
Decision Tree Model
Dr Lotfi Ncib, Associate Professor Of applied mathematics Esprit School of Engineering
lotfi.ncib@esprit.tn
Disclaimer: Some of the Images and content have been taken from multiple online sources and this presentation is intended only for knowledge sharing but not
for any commercial business intention

2. 1
What is The difference between AI, ML and DL?
• Artificial Intelligence AI tries to make computers intelligent in order to mimic
the cognitive functions of humans. So, AI is a general field with a broad scope
including:
• Computer Vision,
• Language Processing,
• Creativity…
• Machine Learning ML is the branch of AI that covers the statistical part of
artificial intelligence. It teaches the computer to solve problems by looking at
hundreds or thousands of examples, learning from them, and then using that
experience to solve the same problem in new situations:
• Regression,
• Classification,
• Clustering…
• DL is a very special field of Machine Learning where computers can actually
learn and make intelligent decisions on their own,
• CNN
• RNN…

3. 2
Types of Machine Learning

4. 3
Classical Machine Learning
F

5. 4
Decision Tree Overview
• Idea: Split data into “pure” regions
Decision
Boundaries

6. 5
What’s Decision Trees
Decision Trees (DTs) are a non-parametric supervised learning method used for classification and regression.
The goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred
from the data features.
Advantages :
❖ Decision Trees are easy to explain. It results
in a set of rules.
❖ It follows the same approach as humans
generally follow while making decisions.
❖ Interpretation of a complex Decision Tree
model can be simplified by its visualizations.
Even a naive person can understand logic.
❖ The Number of hyper-parameters to be
tuned is almost null.
❖ There is a high probability of overfitting in
Decision Tree.
❖ Generally, it gives low prediction accuracy for a
dataset as compared to other machine learning
algorithms.
❖ Information gain in a decision tree with categorical
variables gives a biased response for attributes
with greater number of categories.
❖ Calculations can become complex when there are
many class labels.
Disadvantages :

7. 6
What’s Decision Trees
DecisionTrees
Classification Regression
Target variable has
only two categories
Target variable has
multiple categories
Target is
continuous

8. 7
Decision Tree with its Terminologies
• decision node = test on an attribute
• branch = an outcome of the test
• leaf node = classification or decision
• root = the topmost decision node
• path: a disjunction of test to make the final
decision
Classification on new instances is done by following
a matching path from the root to a leaf node

9. 8
How to build a decision tree?
Top-down tree construction:
• all training data are the root
• data are partitioned recursively based on selected attributes
• bottom-up tree pruning
→ remove subtrees or branches, in a bottom-up manner,
to improve the estimated accuracy on new cases.
• conditions for stopping partitioning:
• all samples for a given node belong to the same class
• there are no remaining attributes for further partitioning
• there are no samples left

10. ❖ID3 (Iterative Dichotomiser 3) is an easy way of decision tree algorithm.
▪ The evaluation that used to build the tree is information gain for splitting criteria.
▪ The growth of tree stops when all samples have the same class or information gain is
not greater than zero. It fails with numeric attributes or missing values.
❖C4.5 is the ID3 improvement or extension It is a mixture of C4.5, C4.5-no-pruning, and C4.5-
rules.
▪ It uses Gain ratio as splitting criteria.
▪ It is an optimal choice with numeric attributes or missing values.
❖CART (Classification - regression tree): is the most popular algorithm in the statistical
community. In the fields of statistics, CART helps decision trees to gain credibility and
acceptance in additional to make binary splits on inputs to get the purpose.
9
There are several algorithms that used to build decision Trees CART, ID3, C4.5, and others.
Decision Trees algorithms

11. 10
Attribute selection measures
Many measures that can be used to determine the optimal direction to split the records as:
❖ Entropy It is a one of the information theory measurement; it detects the impurity of the data set. If the attribute takes
on c different values, then the entropy S related to c-wise classification is defined as equation below:
❖ Information gain It chooses any attribute is used for splitting a certain node. It prioritizes to nominate attributes
having large number of values by calculating the difference in entropy
❖ The gain ratio The information gain equation, G(T,X) is biased toward attributes that have a large number of values over
attributes that have a smaller number of values. These ‘Super Attributes’ will easily be selected as the root, resulted in a broad
tree that classifies perfectly but performs poorly on unseen instances. We can penalize attributes with large numbers of values
by using an alternative method for attribute selection, referred to as Gain Ratio.
𝐺 𝑆, 𝐴 = 𝐸 𝑆 − 𝐸(𝑆, 𝐴)
𝐺𝑎𝑖𝑛𝑅𝑎𝑡𝑖𝑜 𝑆, 𝐴 = 𝐺𝑎𝑖𝑛(𝑆, 𝐴)/𝑆𝑝𝑙𝑖𝑡(𝑆, 𝐴)
𝑆𝑝𝑙𝑖𝑡 𝑆, 𝐴 = − ෍
𝑖=1
𝑛
𝑆𝑖
𝑆
𝑙𝑜𝑔2(
𝑆𝑖
𝑆
)
𝐸 𝑆 = ෍
𝑖=1
𝑐
−𝑝𝑖 𝑙𝑜𝑔2(𝑝𝑖)
Entropy one attribute:
𝐸 𝑆, 𝐴 = − ෍
𝑣𝜖𝐴
𝑆 𝑣
𝑆
𝐸(𝑆 𝑣)
Entropy of two attributes: S is a set of examples

12. 11
Attribute selection measures
Many measures that can be used to determine the optimal direction to split the records as:
❖ Gini Index is a metric to measure how often a randomly chosen element would be incorrectly identified. It means an
attribute with lower Gini index should be preferred.
Comparing Attribute Selection Measures
▪ Information Gain
• Biased towards multivalued attributes
▪ Gain Ratio
• Tends to prefer unbalanced splits in which one partition is much smaller than the other
▪ Gini Index
• Biased towards multivalued attributes ¤ Has difficulties when the number of classes is large
• Tends to favor tests that result in equal-sized partitions and purity in both partitions

13. 12
ID3 operates on whole training set S Algorithm:
1. create a new node
2. If current training set is sufficiently pure:
• Label node with respective class
• We’re done
3. Else:
• x ← the “best” decision attribute for current training set
• Assign x as decision attribute for node
• For each value of x, create new descendant of node
• Sort training examples to leaf nodes
• Iterate over new leaf nodes and apply algorithm recursively
ID3: Algorithm

14. 13
ID3: Classification example
Attributes: Outlook,
Temperature, Humidity, Play,
Class: Play
Shall I play tennis today?

15. 14
 Entropy measures the impurity of S
 S is a set of examples
 p is the proportion of positive examples
 q is the proportion of negative examples
Entropy(S) = - p log2 p - q log2 q
ID3: Entropy

16. 15
Play
No
No
Yes
Yes
Yes
No
Yes
No
Yes
Yes
Yes
Yes
Yes
No
Play
No
No
No
No
No
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
Sort
5 / 14 = 0.36
9 / 14 = 0.64
No
Yes
ID3: Frequency Tables

17. 16
Yes
Yes
No
No
No
Yes
Yes
Yes
Yes
Yes
Yes
Yes
No
No
Sunny Rainy
Humidity
Yes
Yes
Yes
No
No
No
No
Yes
Yes
Yes
Yes
Yes
Yes
No
High Normal
Windy
Yes
Yes
Yes
Yes
Yes
Yes
No
No
Yes
Yes
Yes
No
No
No
False True
Yes
Yes
No
No
Yes
Yes
Yes
Yes
No
No
Yes
Yes
Yes
No
Hot Mild Cool
Outlook
Overcast
Temperature
ID3: Frequency Tables

18. 17
Outlook | No Yes
--------------------------------------------
Sunny | 3 2
--------------------------------------------
Overcast | 0 4
--------------------------------------------
Rainy | 2 3
Temp | No Yes
--------------------------------------------
Hot | 2 2
--------------------------------------------
Mild | 2 4
--------------------------------------------
Cool | 1 3
Humidity | No Yes
--------------------------------------------
High | 4 3
--------------------------------------------
Normal | 1 6
Windy | No Yes
--------------------------------------------
False | 2 6
--------------------------------------------
True | 3 3
Play
ID3: Frequency Tables

19. 18
ID3 Entropy: One Variable
5 / 14 = 0.369 / 14 = 0.64
NoYes
Play
Entropy(Play) = -p log2 p - q log2 q
= - (0.64 * log2 0.64) - (0.36 * log2 0.36)
= 0.94
Example:
Entropy(5,3,2) = - (0.5 * log2 0.5) - (0.3
* log2 0.3) - (0.2 * log2 0.2)= 1.49
So, entropy of whole system before we make our first question is 0.940
Now, we have four features to make decision and they are:
1.Outlook
2.Temperature
3.Windy
4.Humidity

20. 19
Outlook | No Yes
--------------------------------------------
Sunny | 3 2 | 5
--------------------------------------------
Overcast | 0 4 | 4
--------------------------------------------
Rainy | 2 3 | 5
--------------------------------------------
| 14
Size of the set
Size of the subset
E (Play,Outlook) = (5/14)*0.971 + (4/14)*0.0 + (5/14)*0.971
= 0.693
ID3 Entropy: two variables

21. 20
Gain(S, A) = E(S) – E(S, A)
Example:
Gain(Play,Outlook) = 0.940 – 0.693 = 0.247
Information Gain

22. 21
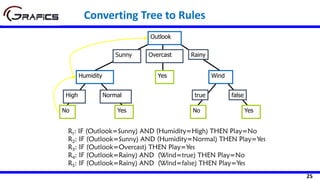
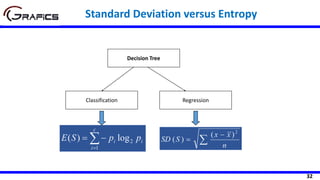
Selecting The Root Node
[2+, 3-]
Outlook
Sunny Rain
[3+, 2-]
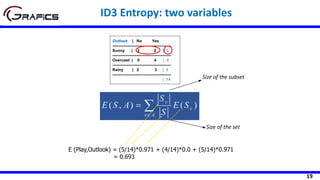
Play=[9+,5-]
E=0.940
Gain(Play,Outlook) = 0.940 –
((5/14)*0.971 + (4/14)*0.0 +
(5/14)*0.971)= 0.247
E=0.971 E=0.971
Overcast
[4+, 0-]
E=0.0
Temp
Hot Cool
[2+, 2-] [3+, 1-]
Play=[9+,5-]
E=0.940
Gain(Play,Temp) = 0.940 –
((4/14)*1.0 + (6/14)*0.918 +
(4/14)*0.811)= 0.029
E=1.0 E=0.811
Mild
[4+, 2-]
E=0.918

23. 22
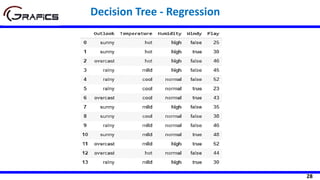
Humidity
High Normal
[3+, 4-] [6+, 1-]
Play=[9+,5-]
E=0.940
Gain(Play,Humidity) = 0.940 – ((7/14)*0.985
+ (7/14)*0.592)= 0.152
E=0.985 E=0.592
Windy
false true
[6+, 2-] [3+, 3-]
Play=[9+,5-]
E=0.940
Gain(Play,Wind) = 0.940 – ((8/14)*0.811 + (6/14)*1.0)
= 0.048
E=0.811 E=1.0
Selecting The Root Node

24. 23
Play
Outlook
Gain=0.247
Windy
Gain=0.048
Humidity
Gain=0.152
Temperature
Gain=0.029
Selecting The Root Node

25. 24
Outlook
Sunny Overcast Rain
Humidity
High Normal
Wind
false true
No Yes
Yes
YesNo
Attribute Node
Value Node
Leaf Node
Decision Tree - Classification

26. 25
R1: IF (Outlook=Sunny) AND (Humidity=High) THEN Play=No
R2: IF (Outlook=Sunny) AND (Humidity=Normal) THEN Play=Yes
R3: IF (Outlook=Overcast) THEN Play=Yes
R4: IF (Outlook=Rainy) AND (Wind=true) THEN Play=No
R5: IF (Outlook=Rainy) AND (Wind=false) THEN Play=Yes
Outlook
Sunny Overcast Rainy
Humidity
High Normal
Wind
true false
No Yes
Yes
YesNo
Converting Tree to Rules

27. 26
Super Attributes
• The information gain equation, G(S,A) is biased toward
attributes that have a large number of values over
attributes that have a smaller number of values.
• Theses ‘Super Attributes’ will easily be selected as the
root, result in a broad tree that classifies perfectly but
performs poorly on unseen instances.
• We can penalize attributes with large numbers of values
by using an alternative method for attribute selection,
referred to as GainRatio(C4.5).
𝐺𝑎𝑖𝑛𝑅𝑎𝑡𝑖𝑜 𝑆, 𝐴 = 𝐺𝑎𝑖𝑛(𝑆, 𝐴)/𝑆𝑝𝑙𝑖𝑡(𝑆, 𝐴) 𝑆𝑝𝑙𝑖𝑡 𝑆, 𝐴 = − ෍
𝑖=1
𝑛
𝑆𝑖
𝑆
𝑙𝑜𝑔2(
𝑆𝑖
𝑆
)

28. 27
||
||
log
||
||
),(
1
2
S
S
S
S
ASSplit i
n
i
i
=
−=
Outlook | No Yes
--------------------------------------------
Sunny | 3 2 | 5
--------------------------------------------
Overcast | 0 4 | 4
--------------------------------------------
Rainy | 2 3 | 5
--------------------------------------------
| 14
Split (Play, Outlook)= - (5/14*log2(5/14)+4/14*log2(4/15)+5/14*log2(5/14))
= 1.577
Gain (Play,Outlook) = 0.247
Gain Ratio (Play,Outlook) = 0.247/1.577 = 0.156
Super Attributes: Example

29. 28
Decision Tree - Regression

30. 29
Standard Deviation and Mean
Players
25
30
46
45
52
23
43
35
38
46
48
52
44
30
SD (Players) = 9.32
Mean (Players) = 39.79

31. 30
Standard Deviation
Outlook
25
30
35
38
48
46
43
52
44
45
52
23
46
30
Sunny Overcast Rainy
SD=7.78
SD=3.49
SD=10.87
Humidity
25
30
46
45
35
52
30
52
23
43
38
46
48
44
High Normal
SD=9.36 SD=8.73
Temperature
25
30
46
44
45
35
46
48
52
30
52
23
43
38
Hot Mild Cool
SD=8.95
SD=7.65
SD=10.51
Windy
25
46
45
52
35
38
46
44
30
23
43
48
52
30
False True
SD=7.87
SD=10.59

32. 31
Outlook | SD Mean
--------------------------------------------
Sunny | 7.78 35.20
--------------------------------------------
Overcast | 3.49 46.25
--------------------------------------------
Rainy | 10.87 39.2
Temp | SD Mean
--------------------------------------------
Hot | 8.95 36.25
--------------------------------------------
Mild | 7.65 42.67
--------------------------------------------
Cool | 10.51 39.00
Humidity | SD Mean
--------------------------------------------
High | 9.36 37.57
--------------------------------------------
Normal | 8.73 42.00
Windy | SD Mean
--------------------------------------------
False | 7.87 41.36
--------------------------------------------
True | 10.59 37.67
Players
Standard Deviation and Mean

33. 32
Standard Deviation versus Entropy
Decision Tree
Classification Regression

34. 33
Decision Tree
Classification Regression
Information Gain versus Standard Error Reduction

35. 34
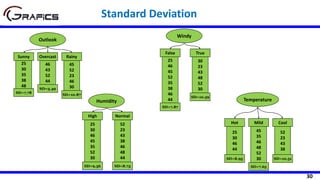
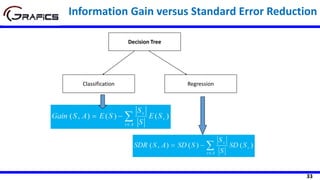
Selecting The Root Node
SDR(Play,Outlook) = 9.32 - ((5/14)*7.78
+ (4/14)*3.49 + (5/14)*10.87)
= 1.662
Outlook
Sunny Rain
[5] [5]
Play=[14]
SD=9.32
SD=7.78 SD=10.87
Overcast
[4]
SD=3.49
Temp
Hot Cool
[4] [4]
Play=[14]
SD=9.32
SD=8.95 SD=10.51
Mild
[6]
SD=7.65
SDR(Play,Temp) =9.32 - ((4/14)*8.95 +
(6/14)*7.65 + (4/14)*10.51)
=0.481

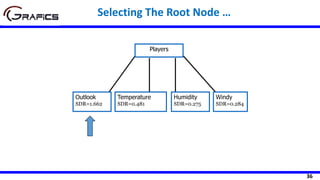
36. 35
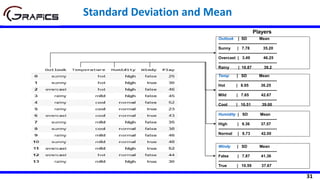
Humidity
High Normal
[7] [7]
Play=[14]
SD= 9.32
SDR(Play,Humidity) =9.32 - ((7/14)*9.36
+ (7/14)*8.73)=0.275
SD=9.36 SD=8.73
Selecting The Root Node …
Windy
Weak Strong
[8] [6]
Play=[14]
SD= 9.32
SD=7.87 SD=10.59
SDR(Play,Humidity) =9.32 - ((8/14)*7.87
+ (6/14)*10.59)=0.284

37. 36
Windy
SDR=0.284
Humidity
SDR=0.275
Players
Outlook
SDR=1.662
Temperature
SDR=0.481
Selecting The Root Node …

38. 37
Outlook
Sunny Overcast Rain
Humidity
High Normal
Wind
Strong Weak
30 45
50
5525
Outlook
Sunny Overcast Rain
Humidity
High Normal
Wind
Strong Weak
30 45
50
5525
Attribute Node
Value Node
Leaf Node
Decision Tree - Regression

39. 38
• are simple, quick and robust
• are non-parametric
• can handle complex datasets
• Decision trees work more efficiently with discrete
attributes
• can use any combination of categorical and
continuous variables and missing values
• sometimes are not easy to be read
• The trees may suffer from overfitting problem
• …
Decision Trees: