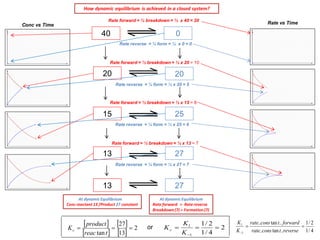
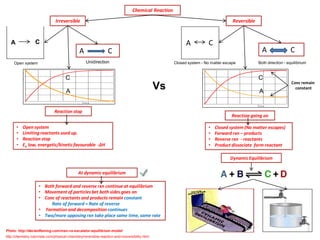
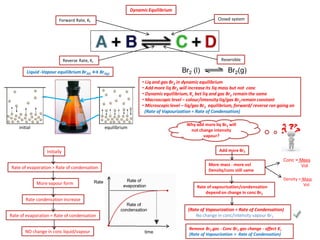
The document discusses dynamic equilibrium in chemical reactions. It explains that in a closed system, reversible reactions proceed in both the forward and reverse directions at the same rate, such that the concentrations of reactants and products remain constant over time. It provides examples of chemical equilibria and how equilibrium is achieved as the reaction progresses through opposing changes in reaction rates and concentrations. Equilibrium constants are also introduced which relate the concentrations of products and reactants at equilibrium.

1. Dynamic Equilibrium
Chemical Reaction
Reversible
Irreversible
A C
•Open system
•Limiting reactants used up.
•Reaction stop
•Ea low, energetic/kinetic favourable -ΔH
C
A C
•Closed system (No matter escapes)
•Forward rxn – products
•Reverse rxn - reactants
•Product dissociate form reactant
C
Reaction going on
Reaction stop
Open system
Unidirection
A
C
Closed system - No matter escape
Both direction - equilibrium
A
C
•Both forward and reverse rxn continue at equilibrium
•Movement of particles bet both sides goes on
•Conc of reactants and products remain constant Rate of forward = Rate of reverse
• Formation and decomposition continues
•Two/more opposing rxn take place same time, same rate
At dynamic equilibrium
Conc remain constant
Vs
A
A
Photo: http://declanfleming.com/man-vs-escalator-equilibrium-model/
http://chemistry.tutorvista.com/physical-chemistry/reversible-reaction-and-irreversibility.html

2. Dynamic Equilibrium
Closed system
Reversible
Forward Rate, Kf
Reverse Rate, Kr
Liquid -Vapour equilibrium Br2(l) ↔ Br2(g)
initial
equilibrium
• Liq and gas Br2 in dynamic equilibrium
• Add more liq Br2 will increase its liq mass but not conc
• Dynamic equilibrium, Kc bet liq and gas Br2 remain the same
• Macroscopic level – colour/intensity liq/gas Br2 remain constant
• Microscopic level – liq/gas Br2 equilibrium, forward/ reverse rxn going on (Rate of Vapourization = Rate of Condensation)
NO change in conc liquid/vapour
Rate of evaporation = Rate of condensation
Rate of evaporation > Rate of condensation
More vapour form
Rate condensation increase
Initially
Br2 (l) Br2(g)
time
Rate
Rate of condensation
Rate of evaporation
Why add more liq Br2 will not change intensity vapour?
Remove Br2 gas - Conc Br2 gas change - affect Kc (Rate of Vapourization > Rate of Condensation)
Density = Mass Vol
Conc = Mass Vol
More mass - more vol Density/conc still same
Rate of vapourization/condensation depend on change in conc Br2
(Rate of Vapourization = Rate of Condensation) No change in conc/intensity vapour Br2
Add more Br2

3. Dynamic Equilibrium
Closed system
Reversible
Forward Rate, Kf
Reverse Rate, Kr
initial
equilibrium
NO change in conc sugar sol
Rate of dissolving = Rate of crystallization
Rate of dissolving > Rate of crystallization
More sugar dissolve - saturated sol form
Rate crystallization increase
Initially
time
Rate
Rate of crystallization
Rate of dissolving
Why add more sugar will not change sweetness/conc?
Solute-solution equilibrium Sugar(s) ↔ Sugar (aq)
• Sugar crystals/solution in dynamic equilibrium
• Add sugar will not increase sugar conc/sweetness (saturated sol)
• Dynamic equilibrium, Kc bet sugar solid and sol remain same
• Macroscopic level – conc/sweetness remain constant
• Microscopic level – crystal/sol in equilibrium, forward/reverse rxn going on (Rate of Dissolving = Rate of Crystallization)
Adding more water – affect Kc – Conc sugar changes ( Rate of Dissolving > Rate of Crystallization )
Sugar (s) Sugar (aq)
Add more sugar
More mass - more vol Density/conc still same
Conc = Mass Vol
Density = Mass Vol
Rate of dissolving/crystallization depend on change in sugar conc
(Rate of Dissolving = Rate of Crystallization) No change in sugar conc (solution)

4. Dynamic Equilibrium
Closed system
Reversible
Forward Rate, Kf
Reverse Rate, Kr
initial
equilibrium
NO change in conc vapour
Rate of vapourization = Rate of crystallization
Rate of vapourization > Rate of crystallization
More iodine sublime
Rate crystallization increase
Initially
time
Rate
Rate of crystallization
Rate of vapourization
Why add more I2 will not change vapour pressure/intensity?
Solid-vapour equilibrium Iodine(s) ↔ Vapour(g)
• I2 solid/vapour in dynamic equilibrium
• Add more I2 will not increase vapour pressure I2
• Equilibrium, Kc bet solid/vapour remain the same (Temp dependent)
• Macroscopic level – Vapour pressure/intensity remain constant
• Microscopic level – solid/vapour in equilibrium, forward/reverse rxn going on (Rate of Vapourization = Rate of Crystallization)
Using a bigger container. Will vapour pressure change?
Iodine (s) Iodine (g)
Add more I2
More mass - more vol Density/conc still same
Conc = Mass Vol
Density = Mass Vol
Rate of vapourization/crystallization depend on change in conc I2 (Temp dependent)
(Rate of Vapourization = Rate of Crystallization)
Vapour pressure same

5. Dynamic Equilibrium
Closed system
Reversible
Forward Rate, Kf
Reverse Rate, Kr
Liquid -Vapour equilibrium Br2(l) ↔ Br2(g)
initial
equilibrium
NO change in conc liquid/intensity vapour/vapour pressure
Rate of evaporation = Rate of condensation
Liquid Br2 evaporate
Macroscopic – no changes
2NO2(g) N2O4(g)
Physical system
Chemical system
Vapour Br2 condense
Forward rate rxn Rate Combining
Backward rate rxn Rate decomposition
Reversible rxn happening, same time with same rate
Rate of forward = Rate of backward
Conc of reactants and products remain UNCHANGED not EQUAL
combining
decomposition
brown
colourless

6. Dynamic Equilibrium
Closed system
Reversible
Forward Rate, Kf
Reverse Rate, Kr
2NO2(g) N2O4(g)
Chemical system
Forward rate rxn Rate Combining
Backward rate rxn Rate dissociation
Reversible rxn happening, same time with same rate
Rate of forward = Rate of backward
Conc of reactant and product remain UNCHANGED/CONSTANT not EQUAL
combining
dissociation
Conc vs time
Rate vs time
Conc
Time
Conc NO2
Conc N2O4
With time
•Conc NO2 decrease ↓ - Forward rate decrease ↓
•Conc N2O4 increase ↑ - Backward rate increase ↑
2NO2(g) N2O4(g)
Forward rate
Backward rate
Forward Rate = Backward Rate
Conc NO2 and N2O4 remain UNCHANGED/CONSTANT
brown
colourless

7. How dynamic equilibrium is achieved in closed system?
Conc of NO2 decrease ↓over time
Forward rate, Kf decrease ↓ over time
Forward Rate = Reverse Rate
NO2
2NO2(g) N2O4(g)
Conc of N2O4 increase ↑ over time
N2O4
Reverse rate, Kr increase ↑ over time
NO2
N2O4
1
2
Conc of reactant/product remain constant
Rate
3
Time
Conc
NO2
N2O4
At dynamic equilibrium
As reaction proceeds concentration
As reaction proceeds rate
Time

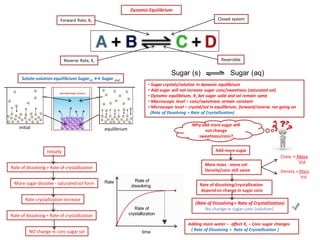
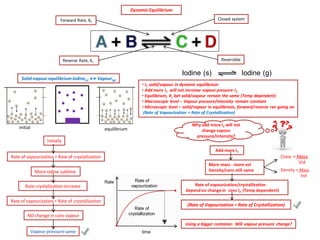
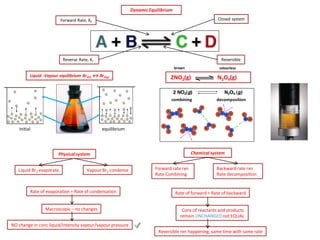
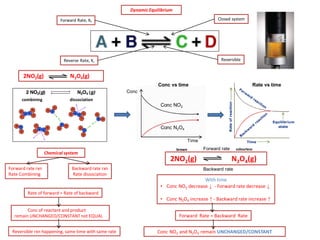
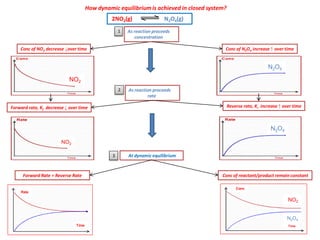
8. Dynamic Equilibrium
Reversible (closed system)
Forward Rate, K1 Reverse Rate, K-1
Kc = ratio of molar conc of product (raised to power of their respective stoichiometry coefficient)
to molar conc of reactant (raised to power of their respective stoichiometry coefficient)
Conc of product and reactant
at equilibrium
At Equilibrium
Forward rate = Backward rate
Conc reactants and products remain
CONSTANT/UNCHANGE
Equilibrium Constant Kc
aA(aq) + bB(aq) cC(aq) + dD(aq)
coefficient
Solid/liq not included in Kc
Conc represented by [ ]
K1
K-1
   
   a b
c d
c
A B
C D
K 
1
1


K
K
Kc
Equilibrium Constant Kc
express in
Conc vs time Rate vs time
A + B
C + D
Conc
Time
Click here notes on dynamic equilibrium
Excellent Notes
K1 = forward rate constant
K-1 = reverse rate constant

9. Large Kc
• Position equilibrium shift to right
• More product > reactant
Magnitude of Kc
   
   a b
c d
c
A B
C D
K 
Extend of reaction
How far rxn shift to right or left?
Not how fast
   
   a b
c d
c
A B
C D
K 
Small Kc
• Position equilibrium shift to left
• More reactant > product
 
 c  K c K
Position of equilibrium
2CO2(g) ↔ 2CO(g) + O2(g)
92 3 10   c K
2H2(g) + O2(g) ↔ 2H2O(g)
81  310 c K
H2(g) + I2(g) ↔ 2HI(g)
2  8.710 c K
1
Moderate Kc
• Position equilibrium lies slightly right
• Reactant and product equal amount
Reaction completion
Reactant favoured Reactant/Product equal Product favoured
c K
Temp
dependent
Extend
of rxn
Not how fast

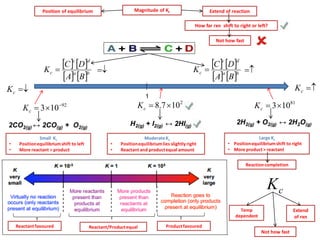
10. Equilibrium Constant Kc
   
   a b
c d
c
A B
C D
K 
aA(aq) + bB(aq) cC(aq) + dD(aq)
Conc of product and reactant at equilibrium
Equilibrium expression HOMOGENEOUS gaseous rxn
4NH3(g) + 5O2(g) ↔ 4NO(g) + 6H2O(g) N2(g) + 3H2(g) ↔ 2NH3(g)
NH4CI(s) ↔ NH3(g) + HCI(g)
2SO2(g) + O2(g) ↔ 2SO3(g)
   
   5
2
4
3
6
2
4
NH O
NO H O
Kc 
 
   3
2
1
2
2
3
N H
NH
Kc 
   1 1
3 K NH HCI c 
   
 0
4
1 1
3
NH CI
NH HCI
Kc 
 
   1
2
2
2
2
3
SO O
SO
Kc 
Equilibrium expression HETEROGENOUS rxn
CaCO3(s) ↔ CaO(g) + CO2(g)
   
 0
3
1
2
1
CaCO
CaO CO
Kc 
   1
2
1 K CaO CO c 
CH3COOH(l) + C2H5OH(l) ↔ CH3COOC2H5(l) + H2O(l)
   
   1
2 5
1
3
1
2
1
3 2 5
CH COOH C H OH
CH COOC H H O
Kc 
Equilibrium expression HOMOGENEOUS liquid rxn
Cu2+
(aq) + 4NH3(aq) ↔ [Cu(NH3)4]2+
   
   4
3
2 1
2
3 4 ( )
Cu NH
Cu NH
Kc



Reactant/product same phase
Reactant/product diff phase
Solid and liq - conc no change
(not included)

11. Conc vs Time
How dynamic equilibrium is achieved in a closed system?
40 0
Rate forward = ½ breakdown = ½ x 40 = 20
Rate reverse = ¼ form = ¼ x 0 = 0
20 20
Rate forward = ½ breakdown = ½ x 20 = 10
Rate reverse = ¼ form = ¼ x 20 = 5
15 25
Rate forward = ½ breakdown = ½ x 15 = 8
Rate reverse = ¼ form = ¼ x 25 = 6
13 27
Rate forward = ½ breakdown = ½ x 13 = 7
Rate reverse = ¼ form = ¼ x 27 = 7
13 27
At dynamic Equilibrium
Rate forward = Rate reverse
Breakdown (7) = Formation (7)
At dynamic Equilibrium
Conc reactant 13 /Product 27 constant
Rate vs Time
1/ 4
1/ 2
.. tan ..
.. tan ..
1
1  
 rate cons t reverse
rate cons t forward
K
  K
 
 
 
2
13
27
tan
  
reac t
product
Kc 2
1/ 4
1/ 2
1
1   
 K
K
Kc or

12. Click here to view simulation
Click here simulation using paper clips
Click here simulation on reversible rxn
Click here on reversible rxn
Simulation on Dynamic equilibrium
Click here on equilibrium constant