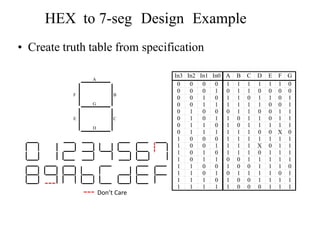
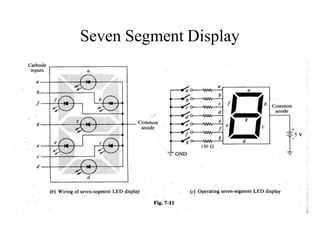
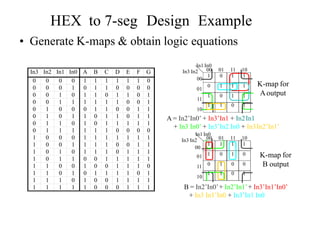
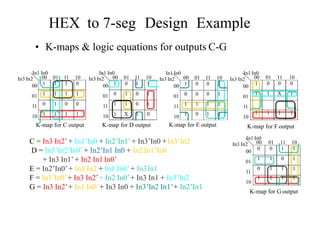
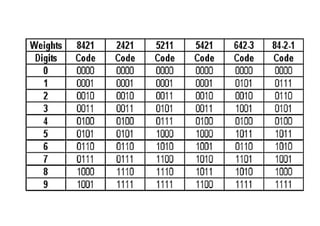
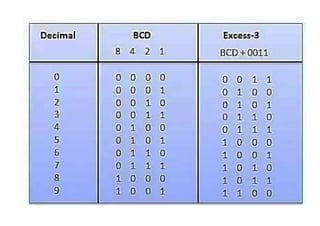
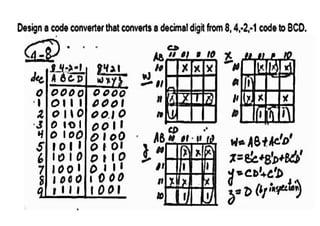
The document describes designing a HEX to 7-segment display decoder using K-maps. It provides the truth table and generates K-maps for each output (A-G) of the 7-segment display. Logic equations are obtained from the K-maps to describe the relationship between the 4 HEX inputs and 7 display outputs.

1. BY UNSA SHAKIR
HEX to 7-seg Design Example
Using K-maps

2. HEX to 7-seg Design Example
• Create truth table from specification
A
B
C
D
E
F
G
In3 In2 In1 In0 A B C D E F G
0 0 0 0 1 1 1 1 1 1 0
0 0 0 1 0 1 1 0 0 0 0
0 0 1 0 1 1 0 1 1 0 1
0 0 1 1 1 1 1 1 0 0 1
0 1 0 0 0 1 1 0 0 1 1
0 1 0 1 1 0 1 1 0 1 1
0 1 1 0 1 0 1 1 1 1 1
0 1 1 1 1 1 1 0 0 X 0
1 0 0 0 1 1 1 1 1 1 1
1 0 0 1 1 1 1 X 0 1 1
1 0 1 0 1 1 1 0 1 1 1
1 0 1 1 0 0 1 1 1 1 1
1 1 0 0 1 0 0 1 1 1 0
1 1 0 1 0 1 1 1 1 0 1
1 1 1 0 1 0 0 1 1 1 1
1 1 1 1 1 0 0 0 1 1 1
Don’t Care

3. Seven Segment Display

4. HEX to 7-seg Design Example
• Generate K-maps & obtain logic equations
00 01 11 10
1 1 1 1
1 0 1 0
0 1 0 0
1 1 0 1
01
11
10
00 01 11 10
1 0 1 1
0 1 1 1
1 0 1 1
1 1 0 1
In1 In0
In3 In2
00
01
11
10
A = In2’In0’ + In3’In1 + In2In1
+ In3 In0’ + In3’In2 In0 + In3In2’In1’
In1 In0
In3 In2
00
B = In2’In0’+ In2’In1’+ In3’In1’In0’
+ In3 In1’In0 + In3’In1 In0
K-map for
Aoutput
K-map for
B output
In3 In2 In1 In0 A B C D E F G
0 0 0 0 1 1 1 1 1 1 0
0 0 0 1 0 1 1 0 0 0 0
0 0 1 0 1 1 0 1 1 0 1
0 0 1 1 1 1 1 1 0 0 1
0 1 0 0 0 1 1 0 0 1 1
0 1 0 1 1 0 1 1 0 1 1
0 1 1 0 1 0 1 1 1 1 1
0 1 1 1 1 1 1 0 0 0 0
1 0 0 0 1 1 1 1 1 1 1
1 0 0 1 1 1 1 0 0 1 1
1 0 1 0 1 1 1 0 1 1 1
1 0 1 1 0 0 1 1 1 1 1
1 1 0 0 1 0 0 1 1 1 0
1 1 0 1 0 1 1 1 1 0 1
1 1 1 0 1 0 0 1 1 1 1
1 1 1 1 1 0 0 0 1 1 1

5. HEX to 7-seg Design Example
• K-maps & logic equations for outputs C-G
00 01 11 10
1 0 0 1
0 0 0 1
1 1 1 1
1 0 1 1
00
01
11
10
In3 In2 00 01 11 10
1 0 0 0
1 1 X 1
1 0 1 1
1 1 1 1
In1 In0
In3 In2
00
01
11
10
K-map for F output
00 01 11 10
0 0 1 1
1 1 0 1
0 1 1 1
1 1 1 1
In1 In0
In3 In2
00
01
11
10
K-map for G output
00 01 11 10
1 1 1 0
1 1 1 1
0 1 0 0
1 1 1 1
00
01
11
10
In3 In2 00 01 11 10
1 0 1 1
0 1 0 1
1 1 0 1
1 X 1 0
00
01
11
10
In3 In2
In1 In0 In1 In0 In1 In0
K-map for C output K-map for D output K-map for E output
C = In3 In2’ + In1’In0 + In2’In1’+ In3’In0 +In3’In2
D = In3’In2’In0’ + In2’In1 In0 + In2In1’In0
+ In3 In1’ + In2 In1In0’
E = In2’In0’+ In3 In2 + In1 In0’ + In3In1
F = In1’In0’+ In3 In2’+ In2 In0’+ In3 In1 + In3’In2
G = In3 In2’+ In1 In0’+ In3 In0 + In3’In2 In1’+ In2’In1

6. K-map for each output and get
A = A’C+A’BD+B’C’D’+AB’C’
B = A’B’+A’C’D’+A’CD+AB’C’
C = A’B+A’D+B’C’D’+AB’C’
D = A’CD’+A’B’C+B’C’D’+AB’C’+A’BC’D
E = A’CD’+B’C’D’
F = A’BC’+A’C’D’+A’BD’+AB’C’
G = A’CD’+A’B’C+A’BC’+AB’C’