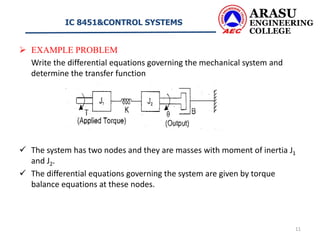
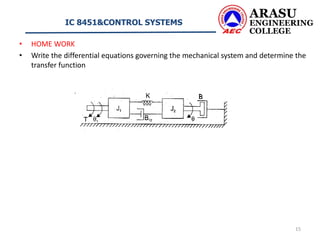
This document discusses rotational mechanical systems and their modeling. It describes how rotational systems can be modeled using three elements: moment of inertia to represent mass, a dashpot to represent friction, and a torsional spring to represent elasticity. It provides the torque balance equations for idealized elements of mass, friction, and elasticity. As an example, it analyzes a two-mass rotational system and derives the differential equations governing its motion and determines its transfer function.

1. IC 8451&CONTROL SYSTEMS
Department of Electrical and Electronics Engineering
Approved by AICTE | Affiliated to Anna University | Accredited by NAAC | Accredited NBA | Recognized by UGC under 2(f) and 12(B)
Chennai Main Road, Kumbakonam- 612 501.
ARASU ENGINEERING COLLEGE
1

2. Prepared by
Mrs.K.Kalpana., M.E.,(Ph.D).,
Department of Electrical and Electronics Engineering
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
2

3.  MECHANICAL ROTATIONAL SYSTEMS
 The model of rotational mechanical systems can be obtained by
using three elements, moment of inertia [J] of mass, dash-pot with
rotational frictional coefficient [B] and torsional spring with
stiffness [K].
 The weight of the rotational mechanical system is represented by the
moment of inertia of the mass.
 The moment of inertia of the system or body is considered to be
concentrated at the centre of gravity of the body.
 The elastic deformation of the body can be represented by a spring
(torsional spring).
 The friction existing in rotational mechanical system can be
represented by the dash-pot.
 The dash-pot is a piston rotating inside a cylinder filled with
viscous fluid.
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
3

4.  When a torque is applied to a rotational mechanical system, it
is opposed by opposing torques due to moment of inertia,
friction and elasticity of the system.
 The torques acting on a rotational mechanical body are
governed by Newton s second law of motion for rotational
systems.
 It states that the sum of torques acting on a body is zero (or
Newton’s law states that the sum of applied torques is equal to
the sum of opposing torques on a body).
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
4

5. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
5
List of symbols used in mechanical rotational
system
θ = Angular displacement, rad
dθ /dt =Angular velocity, rad /s
d2θ / dt2 =Angular acceleration, rad /s2
T =Applied torque, N-m
J =Moment of inertia, kg-m2 / rad
B =Rotational frictional coefficient, N-m / (rad /s)
K =Stiffness of the spring, N –m / rad

6. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
6
Torque balance equations of idealized elements
Consider an ideal mass element shown in fig. which has
negligible friction and elasticity.
The opposing torque due to moment of inertia is proportional to
the angular acceleration.

7. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
7
Consider an ideal frictional element dash-pot shown in fig. which has
negligible moment of inertia and elasticity.
 Let a torque be applied on it. The dashpot will be offer an opposing
torque which is proportional to the angular velocity of the body.

8.  When the dashpot has angular displacement at both the ends
as shown in fig, the opposing torque is proportional to
differential angular velocity.
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
8

9.  Consider an ideal elastic element torsional spring shown in fig
,which has negligible moment of inertia and friction.
 Let a torque be applied on it. The spring will offer an opposing
torque which is proportional to angular displacement of the
body.
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
9

10.  When the spring has angular displacement at both the ends as
shown in figure, the opposing torque is proportional to
differential angular displacement.
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
10

11.  EXAMPLE PROBLEM
Write the differential equations governing the mechanical system and
determine the transfer function
 The system has two nodes and they are masses with moment of inertia J1
and J2.
 The differential equations governing the system are given by torque
balance equations at these nodes.
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
11

12.  Let the angular displacement of mass with moment of inertia
J1 is θ1.The opposing torques acting on J1 marked as TJ1 and Tk
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
12
1

13.  The free body diagram of mass with moment of inertia J2 as
shown in fig. The opposing torques acting on J2 are marked as
Tj2,Tb and Tk
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
13

14. ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
14

15. • HOME WORK
• Write the differential equations governing the mechanical system and determine the
transfer function
ARASU
ENGINEERING
COLLEGE
IC 8451&CONTROL SYSTEMS
15