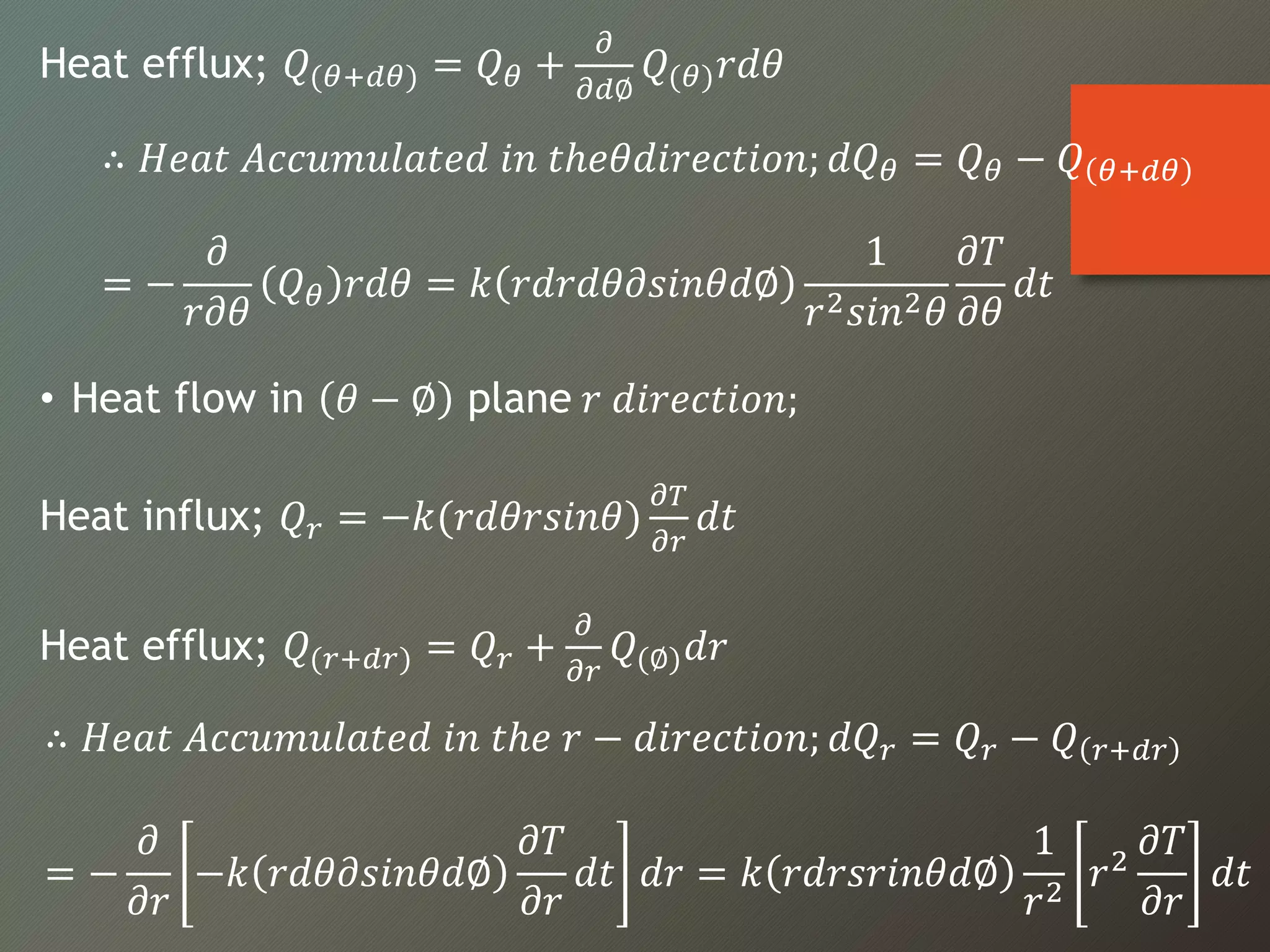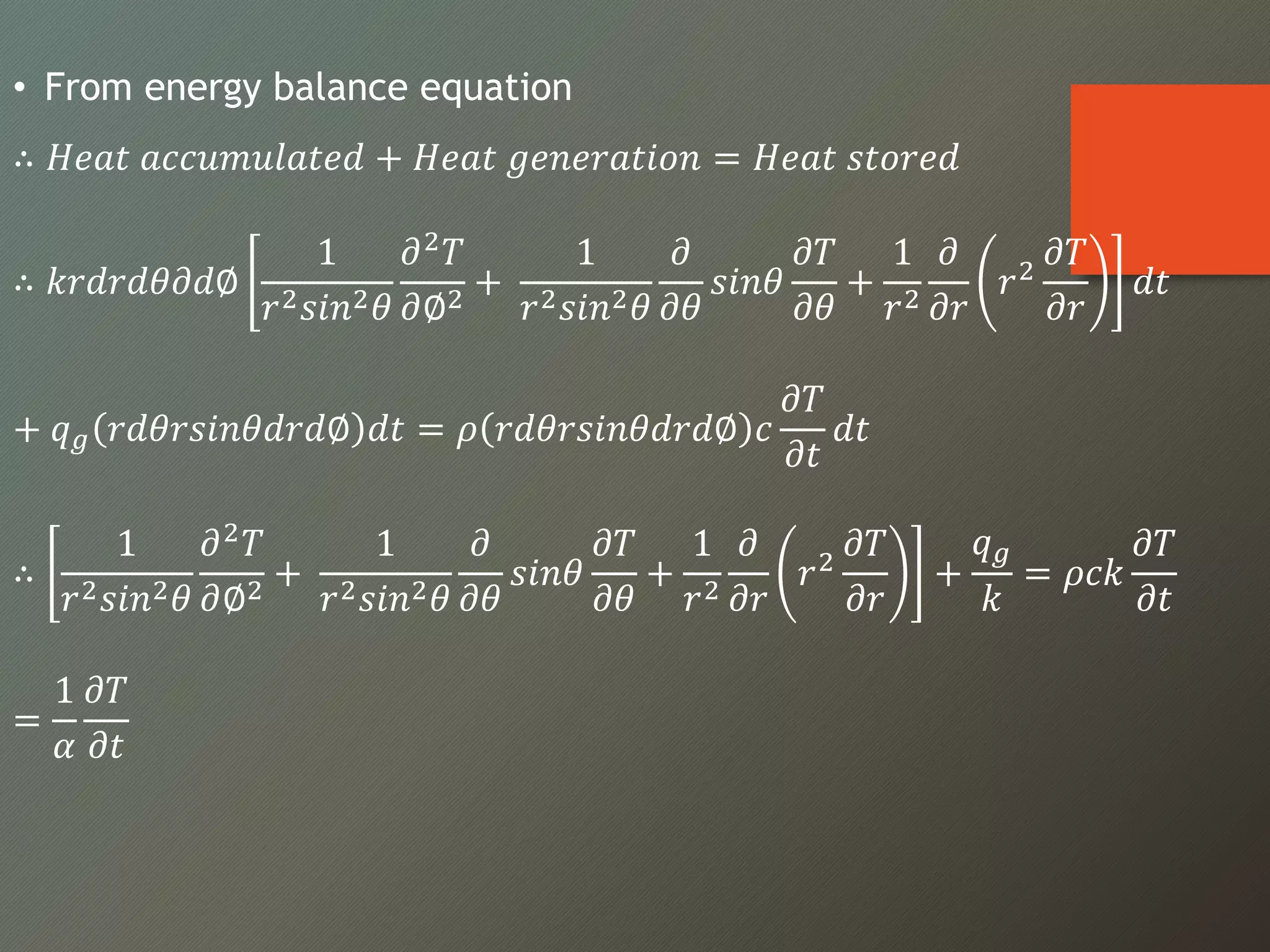Downloaded 102 times
Uploaded byChandresh Suthar
Heat conduction equation
This document discusses heat conduction equations in Cartesian and cylindrical coordinate systems. It presents the general heat conduction equation for a non-homogeneous, anisotropic material undergoing unsteady three-dimensional heat flow. For the Cartesian system, the equation accounts for temperature gradients and thermal conductivity in three dimensions. For the cylindrical system, similar heat accumulation terms are derived for the radial, angular and axial directions. Several simplified cases are also outlined, such as steady-state and one-dimensional heat transfer situations.
More Related Content
Similar to Heat conduction equation
Heat conduction equation
- 1. GANDHINAGAR INSTITUTE OF TECHNOLOGY Heattransfer(2151909) Active learning assignment On Heat conduction Prepared by:- 1). Sonani Manav 140120119223 2). Suthar Chandresh 140120119229 3). Tade Govind 140120119230 Guided by :- Prof . Nikita Gupta
- 2. Content • Heat flowin Cartesian co-ordinate • Heat flow in cylindrical co-ordinate • Heat flow in spherical co-ordinate
- 3. Heat conduction equationin Cartesian co- ordinate system:- 𝐿𝑒𝑡, 𝑇 = 𝑈𝑛𝑖𝑓𝑜𝑟𝑚 𝑡𝑒𝑚𝑝. 𝑎𝑡 𝑡ℎ𝑒 𝑙𝑒𝑓𝑡 𝑓𝑎𝑐𝑒 𝐴𝐵𝐶𝐷 𝑎𝑠 𝑖𝑡 ℎ𝑎𝑠 𝑣𝑒𝑟𝑦 𝑠𝑚𝑎𝑙𝑙 𝑣𝑜𝑙𝑢 𝑑𝑡 𝑑𝑥 = 𝑇𝑒𝑚𝑝. 𝑔𝑟𝑎𝑑𝑖𝑒𝑛𝑡 𝑖𝑛 𝑥 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛 ℃ 𝑚 , 𝑑𝑥 = 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛𝑎𝑙 𝑡ℎ𝑖𝑐𝑘𝑛𝑒𝑠𝑠 𝑜𝑓 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑠, 𝑚, 𝑚 = 𝑚𝑎𝑠𝑠 𝑜𝑓 𝑒𝑙𝑒𝑚𝑒𝑛𝑡; 𝐾𝑔, 𝜌 = 𝑑𝑒𝑛𝑠𝑖𝑡𝑦 𝑜𝑓 𝑚𝑎𝑡𝑒𝑟𝑖𝑎𝑙; 𝑚3 /𝑘𝑔, 𝐴 = 𝐴𝑟𝑒𝑎 𝑜𝑓 𝑒𝑙𝑒𝑚𝑒𝑛𝑡 𝑛𝑜𝑟𝑚𝑎𝑙 𝑡𝑜 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 ℎ𝑒𝑎𝑡 𝑓𝑙𝑜𝑤; 𝑚3 , 𝑐 = 𝑠𝑝𝑒𝑐𝑖𝑓𝑖𝑐 ℎ𝑒𝑎𝑡 𝑜𝑓 𝑚𝑎𝑡𝑒𝑟𝑖𝑎𝑙, 𝜕𝑇 𝜕𝑥 𝑑𝑥 = 𝑐ℎ𝑎𝑛𝑔𝑒 𝑜𝑓 𝑡𝑒𝑚𝑝. 𝑡ℎ𝑟𝑜𝑢𝑔ℎ 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒 𝑑𝑥 𝑖𝑛 𝑥 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛 , 𝑇 + 𝜕𝑇 𝜕𝑥 𝑑𝑥 = 𝑇𝑒𝑚𝑝. 𝑎𝑡 𝐸𝐹𝐺𝐻 𝑓𝑎𝑐𝑒 , 𝑘 𝑥, 𝑘 𝑦, 𝑘 𝑧 = 𝑡ℎ𝑒𝑟𝑚𝑎𝑙 𝑐𝑜𝑛𝑑𝑢𝑐𝑡𝑖𝑣𝑖𝑡𝑦 𝑜𝑓 𝑤𝑎𝑙𝑙 𝑚𝑎𝑡𝑒𝑟𝑖𝑎𝑙 𝑖𝑛 𝑥, 𝑦, 𝑧 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛 , 𝑄 · 𝑔 = 𝐻𝑒𝑎𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑒𝑑 𝑖𝑛 𝑢𝑛𝑖𝑡 𝑡𝑖𝑚𝑒, 𝑊 , 𝑞 · 𝑔 = ℎ𝑒𝑎𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑒𝑑 𝑝𝑒𝑟 𝑢𝑛𝑖𝑡 𝑣𝑜𝑙𝑢𝑚𝑒 𝑝𝑒𝑟 𝑢𝑛𝑖𝑡 𝑡𝑖𝑚𝑒; 𝑊 𝑚3 , 𝑑𝑡 = 𝑒𝑙𝑒𝑚𝑒𝑛𝑡 𝑡𝑖𝑚𝑒 𝑑𝑢𝑟𝑎𝑡𝑖𝑜𝑛,
- 4. • Energy balanceequation for element volume is obtained from the first law of thermodynamics; 𝑁𝑒𝑡 ℎ𝑒𝑎𝑡𝑎𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑜𝑛 𝑓𝑟𝑜𝑚 𝑎𝑙𝑙 𝑡ℎ𝑒 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛(𝐴) + Internal heat generation B = {Heat stored in body(C)} • Heat flow at ABCD face, 𝑄 = −𝑘𝐴 𝑑𝑡 𝑑𝑥 , 𝐴 = 𝑑𝑦. 𝑑𝑧 ∴ 𝑄 = −𝑘 𝑑𝑦. 𝑑𝑧 𝑑𝑡 𝑑𝑥 𝑑𝑡 • Heat flow at EFGH, 𝑄′ = 𝑄 + 𝜕𝑄 𝜕𝑥 𝑑𝑥
- 5. • Total heatAccumulate in 𝑥 direction; 𝑑𝑄 𝑥 = 𝑄′ − 𝑄 = − 𝜕𝑄 𝜕𝑥 𝑑𝑥 = − 𝜕 𝜕𝑥 −𝑘 𝑥 𝑑𝑦. 𝑑𝑧 𝑑𝑇 𝑑𝑥 𝑑𝑥𝑑𝑡 𝑑𝑄 𝑥 = 𝜕 𝜕𝑥 𝑘 𝑥 𝑑𝑇 𝑑𝑥 d𝑥𝑑𝑦𝑑𝑧dt • Similarly, For Y And Z direction, 𝑑𝑄 𝑦 = 𝜕 𝜕𝑦 𝑘 𝑦 𝑑𝑇 𝑑𝑦 d𝑥𝑑𝑦𝑑𝑧dt 𝑑𝑄 𝑧 = 𝜕 𝜕𝑧 𝑘 𝑧 𝑑𝑇 𝑑𝑧 d𝑥𝑑𝑦𝑑𝑧dt
- 6. • Net Heataccumulation in the wall = 𝜕 𝜕𝑥 𝑘 𝑥 𝑑𝑇 𝑑𝑥 + 𝜕 𝜕𝑦 𝑘 𝑦 𝑑𝑇 𝑑𝑦 +
- 7. • This isknown as general heat conduction equation for “NON-HOMOGENEOUS ANISTROPIC MATERIAL”, “Self heat generating”, ‘unsteady three-dimensional heat flow’. • Heat conduction equation for constant thermal conductivity(k): In case of homogeneous and isotropic material, 𝑘 𝑥 = 𝑘 𝑦 = 𝑘 𝑧 = 𝑘 and equation becomes 𝜕2 𝑡 𝜕𝑥2 + 𝜕2 𝑡 𝜕𝑦2 + 𝜕2 𝑡 𝜕𝑧2 + 𝑞 𝑔 k = 𝜌𝑐 𝑘 𝜕𝑡 𝜕𝜏 = 1 𝛼 𝜕𝑡 𝜕𝜏 Where 𝛼 = k 𝜌𝑐 = Thermal conductivity Thermal capacity ; m2 sec The ter𝑚, 𝛼 = k 𝜌𝑐 is known as thermal diffusivity
- 8. • Other simplifiedforms of heat conduction equations: Case 1: When no internal source of heat generation is present eqn. reduce to • 𝑞 𝑔 = 0 𝜕2 𝑡 𝜕𝑥2 + 𝜕2 𝑡 𝜕𝑦2 + 𝜕2 𝑡 𝜕𝑧2 = 1 𝛼 𝜕𝑡 𝜕𝜏 Case 2: When the conduction takes place in the steady state ∴ 𝜕𝑡 𝜕𝜏 = 0 ∴ 𝜕2 𝑡 𝜕𝑥2 + 𝜕2 𝑡 𝜕𝑦2 + 𝜕2 𝑡 𝜕𝑧2 + 𝑞 𝑔 k = 0
- 9. Case 3: Steadystate and one dimensional heat transfer: ∴ 𝜕2 𝑡 𝜕𝑥2 + 𝑞 𝑔 k = 0 Case 4: Steady state one dimensional, without internal heat generation; ∴ 𝜕2 𝑡 𝜕𝑥2 = 0 Case 5: Steady state, two dimensional, without internal heat generation: ∴ 𝜕2 𝑡 𝜕𝑥2 + 𝜕2 𝑡 𝜕𝑦2 = 0 Case 6: Unsteady state, One dimensional, without internal heat generation: ∴ 𝜕2 𝑡 𝜕𝑥2 = 1 𝛼 𝜕𝑡 𝜕𝜏
- 10. Heat conduction equationin cylindrical co- ordinates • While dealing with heat transfer through pipe, wires, rods it is convenient to use cylindrical co-ordinates (𝑟, 𝜃, 𝑧) • Volume of element cylinder = 𝑟. 𝑑𝜃 𝑑𝑟𝑑𝑧 • For cylinder, k = 𝑡ℎ𝑒𝑟𝑚𝑎𝑙 𝑐𝑜𝑛𝑑𝑢𝑐𝑡𝑖𝑣𝑖𝑡𝑦 𝑐 = 𝑠𝑝𝑒𝑐𝑖𝑓𝑖𝑐 ℎ𝑒𝑎𝑡 𝜌 = 𝑑𝑒𝑛𝑠𝑖𝑡𝑦 𝑞 · 𝑔 = ℎ𝑒𝑎𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑒𝑑 𝑝𝑒𝑟 𝑢𝑛𝑖𝑡 𝑡𝑖𝑚𝑒
- 11. Net heat accumulatedin the cylinder due to conduction of heat • Heat flow in 𝑥 − 𝜃 plane, Heat influx; 𝑄 𝑓 = −𝑘𝐴 𝑑𝑇 𝑑𝑟 𝑑𝑡 = −𝑘𝐴 𝑟𝑑𝜃. 𝑑𝑧 𝑑𝑇 𝑑𝑟 𝑑𝑡 Heat efflux; 𝑄(𝑟+𝑑𝑟) = 𝑄(𝑟) + 𝜕 𝜕𝑟 𝑄(𝑟)dr Heat accumulate; 𝑑𝑄 𝑟+𝑑𝑟 = 𝑄(𝑟) − 𝑄 𝑟+𝑑𝑟 = 𝑘𝑟𝑑𝜃𝑑𝑧 𝜕2 𝑇 𝜕𝑟2 +
- 12. • Heat accumulatedin the element; 𝑑𝑄 𝜃 = 𝑄 𝜃 − 𝑄 𝜃−𝑑𝜃 = 𝑘(𝑟𝑑𝑟𝑑𝑧𝑑𝜃) 𝜕2 𝑇 𝑟2 𝜕𝜃2 𝑑𝑡 • Heat flow in 𝑟 − 𝜃 plane; Heat in flux 𝑄 𝑧 = −𝑘 𝑟𝑑𝑟𝑑𝜃 𝜕𝑇 𝜕𝑧 𝑑𝑡 Heat efflux; 𝑄(𝑧+𝑑𝑧) = −𝑘 𝑟𝑑𝑟𝑑𝜃 𝜕𝑇 𝜕𝑧 𝑑𝑡 + 𝜕 𝜕𝑧 𝑄 𝑧 𝑑𝑧 Net heat accumulation in 𝑧-direction ; 𝑑𝑄 𝑧 = 𝑄 𝑧 − 𝑄 𝑧+𝑑𝑧 = 𝑘 𝑟𝑑𝑟𝑑𝜃𝑑𝑧 𝜕2 𝑇 𝜕𝑧2 𝑑𝑡 • Heat Accumulate in cylinder; = 𝑘𝑟𝑑𝑟𝑑𝜃𝑑𝑧 𝜕2 𝑇 𝜕𝑟2 + 1 𝑟 𝜕𝑇 𝜕𝑟 + 𝜕2 𝑇 𝑟2 𝜕𝜃2 +
- 13. • Energy storedin cylinder 𝑒𝑛𝑒𝑟𝑔𝑦 = 𝑚𝑐∆𝑇 = 𝜌 ∙ 𝑣𝑜𝑙𝑢𝑚𝑒 ∙ 𝑐 ∙ 𝜕𝑇 𝜕𝑡 𝑑𝑡 = 𝜌 𝑟𝑑𝜃𝑑𝑟𝑑𝑧 𝑐 𝜕𝑇 𝜕𝑡 𝑑𝑡 • Heat generated = 𝑞 𝑔 𝑟𝑑𝑟𝑑𝜃𝑑𝑧 𝑑𝑡 = 𝐻𝑒𝑎𝑡 𝑎𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑑 + 𝐻𝑒𝑎𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 = 𝐻𝑒𝑎𝑡 𝑠𝑡𝑜𝑟𝑒𝑑 ∴ 𝑘𝑟𝑑𝑟𝑑𝜃𝑑𝑧 𝜕2 𝑇 𝜕𝑟2 + 1 𝑟 𝜕𝑇 𝜕𝑟 + 𝜕2 𝑇 𝑟2 𝜕𝜃2 + 𝜕2 𝑇 𝜕𝑧2 + 𝑞 𝑔 𝑟𝑑𝑟𝑑𝜃𝑑𝑧 𝑑𝑡 = 𝜌 𝑟𝑑𝜃𝑑𝑟𝑑𝑧 𝑐 𝜕𝑇 𝜕𝑡 𝑑𝑡 ∴ 𝜕2 𝑇 𝜕𝑟2 + 1 𝑟 𝜕𝑇 𝜕𝑟 + 𝜕2 𝑇 𝑟2 𝜕𝜃2 + 𝜕2 𝑇 𝜕𝑧2 + 𝑞 𝑔 k = 𝜌𝑐 𝜕𝑇 𝜕𝑡 • This equation is known as, general equation for non homogeneous/ anisotropic material for cylindrical co- ordinates.
- 14. General heat conductionequation for spherical co-ordinates system • While dealing with problems of heat conduction having a spherical geometry. It is convenient to use spherical co-ordinates system;
- 15. • Heat flowthrough • Heat flow in 𝑟 − 𝜃 plane ∅ 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛; Heat influx; 𝑄∅ = −𝑘(𝑟𝑑𝑟𝑑𝜃) 𝜕𝑇 𝜕𝑠𝑖𝑛𝜃𝑑∅ 𝑑𝑡 Heat efflux; 𝑄(∅+𝑑∅) = 𝑄∅ + 𝜕 𝜕𝑠𝑖𝑛𝜃𝑑∅ 𝑄(∅) 𝑟𝑠𝑖𝑛𝜃𝑑∅ ∴ 𝐻𝑒𝑎𝑡 𝐴𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑑 𝑖𝑛 𝑡ℎ𝑒 ∅𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛; 𝑑𝑄∅ = − 𝜕 𝜕𝑠𝑖𝑛𝜃𝑑∅ 𝑄∅ 𝑟𝑠𝑖𝑛𝜃𝑑∅ = 𝑘(𝑟𝑑𝑟𝑑𝜃𝜕𝑠𝑖𝑛𝜃𝑑∅) 𝜕2 𝑇 𝑟2 𝑠𝑖𝑛2 𝜃𝜕𝜃2 𝑑𝑡 • Heat flow in 𝑟 − ∅ plane 𝜃 − 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛 Heat influx; 𝑄 𝜃 = −𝑘(𝑟𝑑𝑟𝑠𝑖𝑛𝜃𝑑𝜃) 𝜕𝑇 𝜕𝑠𝑑𝜃 𝑑𝑡
- 16. Heat efflux; 𝑄(𝜃+𝑑𝜃)= 𝑄 𝜃 + 𝜕 𝜕𝑑∅ 𝑄(𝜃) 𝑟𝑑𝜃 ∴ 𝐻𝑒𝑎𝑡 𝐴𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑑 𝑖𝑛 𝑡ℎ𝑒𝜃𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛; 𝑑𝑄 𝜃 = 𝑄 𝜃 − 𝑄 𝜃+𝑑𝜃 = − 𝜕 𝑟𝜕𝜃 𝑄 𝜃 𝑟𝑑𝜃 = 𝑘 𝑟𝑑𝑟𝑑𝜃𝜕𝑠𝑖𝑛𝜃𝑑∅ 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕𝑇 𝜕𝜃 𝑑𝑡 • Heat flow in 𝜃 − ∅ plane 𝑟 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛; Heat influx; 𝑄 𝑟 = −𝑘(𝑟𝑑𝜃𝑟𝑠𝑖𝑛𝜃) 𝜕𝑇 𝜕𝑟 𝑑𝑡 Heat efflux; 𝑄(𝑟+𝑑𝑟) = 𝑄 𝑟 + 𝜕 𝜕𝑟 𝑄(∅) 𝑑𝑟 ∴ 𝐻𝑒𝑎𝑡 𝐴𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑑 𝑖𝑛 𝑡ℎ𝑒 𝑟 − 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛; 𝑑𝑄 𝑟 = 𝑄 𝑟 − 𝑄 𝑟+𝑑𝑟 = − 𝜕 𝜕𝑟 −𝑘 𝑟𝑑𝜃𝜕𝑠𝑖𝑛𝜃𝑑∅ 𝜕𝑇 𝜕𝑟 𝑑𝑡 𝑑𝑟 = 𝑘 𝑟𝑑𝑟𝑠𝑟𝑖𝑛𝜃𝑑∅ 1 𝑟2 𝑟2 𝜕𝑇 𝜕𝑟 𝑑𝑡
- 17. • Net heataccumulated in the sphere = 𝑘𝑟𝑑𝑟𝑑𝜃𝜕𝑑∅ 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕2 𝑇 𝜕∅2 + 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕 𝜕𝜃 𝑠𝑖𝑛𝜃 𝜕𝑇 𝜕𝜃
- 18. • From energybalance equation ∴ 𝐻𝑒𝑎𝑡 𝑎𝑐𝑐𝑢𝑚𝑢𝑙𝑎𝑡𝑒𝑑 + 𝐻𝑒𝑎𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 = 𝐻𝑒𝑎𝑡 𝑠𝑡𝑜𝑟𝑒𝑑 ∴ 𝑘𝑟𝑑𝑟𝑑𝜃𝜕𝑑∅ 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕2 𝑇 𝜕∅2 + 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕 𝜕𝜃 𝑠𝑖𝑛𝜃 𝜕𝑇 𝜕𝜃 + 1 𝑟2 𝜕 𝜕𝑟 𝑟2 𝜕𝑇 𝜕𝑟 𝑑𝑡 + 𝑞 𝑔 𝑟𝑑𝜃𝑟𝑠𝑖𝑛𝜃𝑑𝑟𝑑∅ 𝑑𝑡 = 𝜌 𝑟𝑑𝜃𝑟𝑠𝑖𝑛𝜃𝑑𝑟𝑑∅ 𝑐 𝜕𝑇 𝜕𝑡 𝑑𝑡 ∴ 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕2 𝑇 𝜕∅2 + 1 𝑟2 𝑠𝑖𝑛2 𝜃 𝜕 𝜕𝜃 𝑠𝑖𝑛𝜃 𝜕𝑇 𝜕𝜃 + 1 𝑟2 𝜕 𝜕𝑟 𝑟2 𝜕𝑇 𝜕𝑟 + 𝑞 𝑔 𝑘 = 𝜌𝑐𝑘 𝜕𝑇 𝜕𝑡 = 1 𝛼 𝜕𝑇 𝜕𝑡