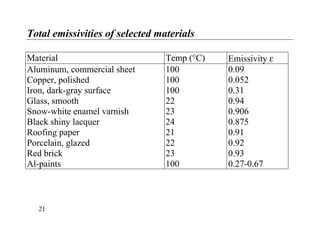
- Thermal radiation is electromagnetic radiation emitted by a body as a result of its temperature and is restricted to a limited range of the electromagnetic spectrum. - Blackbody radiation obeys certain simple laws like Stefan-Boltzmann's law and Planck distribution law that describe how radiation is emitted at different wavelengths and temperatures. - Real surfaces emit and absorb less radiation than blackbodies and their emissivity is usually less than 1.

1. Radiation

2. Radiation
Thermal radiation.:
”That electromagnetic radiation emitted by a body as a result
of its temperature”.
Thermal radiation is restricted to a limited range of the
electromagnetic spectrum.
2

3. Radiation
fig. 8.1 i Holman
3

4. Blackbody radiation
A blackbody is a perfect radiator.
Three characteristics:
•It absorbs all incident radiation
•It radiates more energy than any real surface at the same
temperature
•The emitted radiation is independent of direction
Also:
Blackbody radiation obey certain simple laws
4

5. Stefan-Boltzmann’s law
The total power radiated from a blackbody is calculated from
Stefan-Boltzmann´s law:
Eb = σ⋅T4
where Eb = total power radiated per unit area from
a blackbody (W/m2
)
σ = 5.669 ⋅ 10-8
W/(m2
⋅K4
). (Stefan-Boltzmann
constant)
T = absolute temperature (K)
5

6. Planck distribution law
The wavelength distribution of emitted blackbody radiation is
determined from the Planck distribution law:
[ ]
E T
C
C T
bλ λ
λ λ
, ( , )
exp( / ( ))
=
⋅ ⋅
1
5
2 1−
where C1 = 2π⋅h⋅co
2
= 3.742⋅108
W⋅µm4
/ m2
C2 = (h⋅co / k) =1.439 ⋅ 104
µm K
λ = wavelength (µm)
T = absolute temperature (T)
h = Planck constant
6

7. k = Boltzmann constant
c0 = speed of light in vacuum
7

8. Result of increasing temperature on radiation
•Higher intensity
•Shorter wavelength higher frequency
8

9. Wien’s displacement law
The wavelength of maximum emissive power is determined
by Wien’s displacement law:
λmax ⋅ T = C3 = 2897.8 µm K
9

10. Radiation from real surfaces
Real surfaces:
•emit and absorb less than blackbodies
•reflect radiation
•emit and absorb differently depending on angle and
wavelength
•do not obey the simple laws
10

11. Fig. 12.16 i Incropera
11

12. Spectral emissivity and total emissivity
To account for ”real surface”- behavior we introduce the
spectral emissivity, defined by
Eλ(λ,T) = ελ(λ,T) ⋅ Eλ,black (λ,T)
and the total emissivity defined by
E = ε ⋅ Eb = ε ⋅ σ ⋅ T4
(ε = integrated average)
12

13. Gray diffuse body
To simplify matters it is common to assume the emissivity to
be independent on wavelength and direction. Such a surface is
called a gray diffuse body, for which
Eλ(λ,T) = ελ ⋅ Eλ,black (λ,T)
ελ = constant = ε (0 < ε < 1)
13

14. Absorptivity, reflectivity, transmittivity
Incident radiation may be absorbed, reflected or transmitted
We define
Absorptivity α: Fraction of incident radiation absorbed
Reflectivity ρ: Fraction of incident radiation reflected
Transmittivity τ: Fraction of incident radiation transmitted
thus α + ρ + τ = 1
14
τ
α
ρ

15. Kirchhoff’s identity
The (total) emissivity and the (total) absorptivity of a surface
are equal at equal temperatures:
ε = α
15

16. Radiation exchange between blackbodies
To calculate radiation exchange we must take into account
•surface areas
•surface geometries
•position in relation to each other
This is done by the shape factor, F12
F12 = fraction of radiation leaving surface 1 intercepted
1
2
by surface 2.
16

17. Net exchange of radiation, law of reciprocity
Net exchange of radiation between blackbodies:
q1-2 = F12 ⋅ A1 ⋅ (Eb1 -Eb2) = F12 ⋅ A1 ⋅ σ ⋅ (T1
4
- T2
4
)
Law of reciprocity
F12 ⋅ A1 ⋅ = F21 ⋅ A2
17

18. Shape factors
Shape factors are often difficult to calculate
See diagrams and formulas in
Holman, Figs 8.12-8.16 and
CFT pp. 45-47
Important special case:
Small (convex) surface (1) surrounded by other surface (2):
F12 = 1.
18

19. Radiation exchange between real surfaces, simple case
For the special case of F12 = 1 the exchange is calculated as
q1-2 = ε1 ⋅ A1 ⋅ (Eb1 -Eb2) = ε1 ⋅ A1 ⋅ σ ⋅ (T1
4
- T2
4
)
Comparing to Newton’s law of cooling:
q = hr ⋅ A1 ⋅ (T1 -T2)
hr = ε1 ⋅ σ ⋅ (T1
4
- T2
4
) / (T1 - T2) = ε1 ⋅ hr, black
hr, black = f(T1, T2), from table!
A1
F12 = ε1
19

20. Table p.30 in CFT
20

21. Total emissivities of selected materials
Material Temp (°C) Emissivity ε
Aluminum, commercial sheet 100 0.09
Copper, polished 100 0.052
Iron, dark-gray surface 100 0.31
Glass, smooth 22 0.94
Snow-white enamel varnish 23 0.906
Black shiny lacquer 24 0.875
Roofing paper 21 0.91
Porcelain, glazed 22 0.92
Red brick 23 0.93
Al-paints 100 0.27-0.67
21

22. Radiation exchange calculated by resistance networks
Consider the blackbody emissive power as the driving
potential
q1-2 = (Eb1 -Eb2) / Rrad = σ ⋅ (T1
4
-T2
4
) / Rrad
Consider the radiation resistance as the sum of surface and
space resistances
Rrad = Rsurface1 + Rspace + Rsurface2
J2J1
Eb1 Eb2
Rsurface1 Rspace Rsurface2
22

23. Radiation exchange by resistance networks, assumptions
Assume:
•All surfaces are gray,
•All surfaces are uniform in temperature.
•Reflective and emissive properties are constant over the
surfaces.
Define:
•Irradiation, G = total radiation / (unit time, unit area)
•Radiosity, J = total radiation leaving /(unit time, unit area)
(including reflected radiation)
Assume these properties are uniform over each surface.
23

24. Surface resistance:
Radiosity = emitted radiation + radiation reflected:
J = ε ⋅ Eb + ρ ⋅ G
where ε = emissivity
ρ = reflectivity of surface
Assume surfaces opaque (τ=0)
=> ρ = 1 - α = 1 - ε
(as α = ε).
=> J = ε⋅ Eb + (1 - ε) ⋅ G
or G = (J - ε ⋅ Eb) / (1 - ε)
24

25. The net energy leaving the surface per unit area:
q / A = J - G = ε⋅ Eb + (1 - ε) ⋅ G - G =
=ε ⋅ Eb - ε ⋅ G = ε ⋅ (Eb -G)
=>
q
A
E J
E J
Ab
b
=
⋅
−
⋅ − =
−
− ⋅
ε
ε ε ε1 1
( )
( )
( ) / ( )
Consider (Eb - J) as the driving potential.
=> Rsurface = (1-ε)/(ε ⋅ A)
25

26. Space resistance:
Radiation from 1 to 2 (per unit time): J1⋅A1⋅F12 .
Radiation from 2 to 1 (per unit time): J2⋅A2⋅F21.
Net exchange of radiation:
q12 = J1⋅A1⋅F12 - J2⋅A2⋅F21 = (J1 -J2)⋅A1⋅F12 = (J1 -J2)⋅A2⋅F21
(as A1⋅F12 = A2⋅F21 ).
Consider (J1 -J2) as the driving potential,
=> Rspace = 1/(A1⋅F12)
26

27. Heat exchange due to radiation, two bodies
q
E E
R
E E
R R R
T T
A A F A
b b
rad
b b
surface space surface
=
−
=
−
+ +
=
⋅ −
−
⋅
+
⋅
+
−
⋅
1 2 1 2
1 2
1
4
2
4
1
1 1 1 12
2
2 2
1 1 1
σ
ε
ε
ε
ε
( )
27

28. Special case, two parallel infinite plates
F12 = 1 and A1 = A2
q
A
T T
=
⋅ −
+ −
σ
ε ε
( )1
4
2
4
1 2
1 1
1
Special case, two concentric cylinders or spheres
F12 = 1
q
A
T T
A
A
1
1
4
2
4
1
1
2 2
1 1
1
=
⋅ −
+ ⋅ −
σ
ε ε
( )
( )
If A1 <<A2 q /A1 = ε1 ⋅ σ ⋅ (T1
4
- T2
4
)
28

29. Three body problem
•Calculate all resistances.
•For the nodes J1, J2 and J3, the sum of the energy flows into
each of the nodes must be zero.
Example, node J1
E J J J− −
J2J1
J3
Eb
Rspace12
Rspace23Rspace13
Rsurface
Rsurface
Rsurface
A
A F
J J
A F
b1 1
1
1 1
2 1
1 12
3 1
1 131
0
−
⋅






+
⋅
+
−
⋅
=
⋅
ε
ε
EbEb
•Solve J1 -J3 !
•Calculate the heat exchanges!
29

30. Radiation shields
q
A
T T
=
⋅ −
+ −
σ
ε ε
( )
/ /
1
4
2
4
1 21 1 1
1 2
No shield
1 23
With shield
(q/A)1-3(q/A)13
(q/A)1-3 = (q/A)3-2 = (q/A)
q
A
T T T T
=
⋅ −
+ −
=
⋅ −
+ −
σ
ε ε
σ
ε ε
( )
/ /
( )
/ /
1
4
3
4
1 3
3
4
2
4
3 21 1 1 1 1 1
Everything is known except the temperature T3.
30

31. Simplest case, all emissivities equal:
T1
4
- T3
4
= T3
4
- T2
4
=> T3
4
= ½ ⋅ (T1
4
+ T2
4
)
=>
q
A
T T
=
⋅ ⋅ −
+ −
1
2 1
4
2
4
3 21 1 1
σ
ε ε
( )
/ /
Emissivities assumed equal, => heat flux reduced to half
31

32. Multiple shields of equal emissivities
It may be shown by similar reasoning that the heat flux will
be reduced to
(q / A) =
1
n +1
(q / A)with shields without shields⋅
where n is the number of shields.
32

33. 33
Different emissivities
Two plates with equal emissivities ε1
One shield of different emissivity ε2:
1
2
−1
(q / A) =
2
(q / A)with shields without shields
1
⋅
+ −
ε
ε ε 11 1
1 2
ε2 << ε1 => largest decrease in heat flux
Assume ε1 = 1. =>
1
(q / A) =
2
(q / A) (q / A)with shields without shields without shields⋅
−
+ −
= ⋅ ⋅
2 1
1 1
1
21 2
2ε
ε
thus equal to one half the emissivity of the shield.