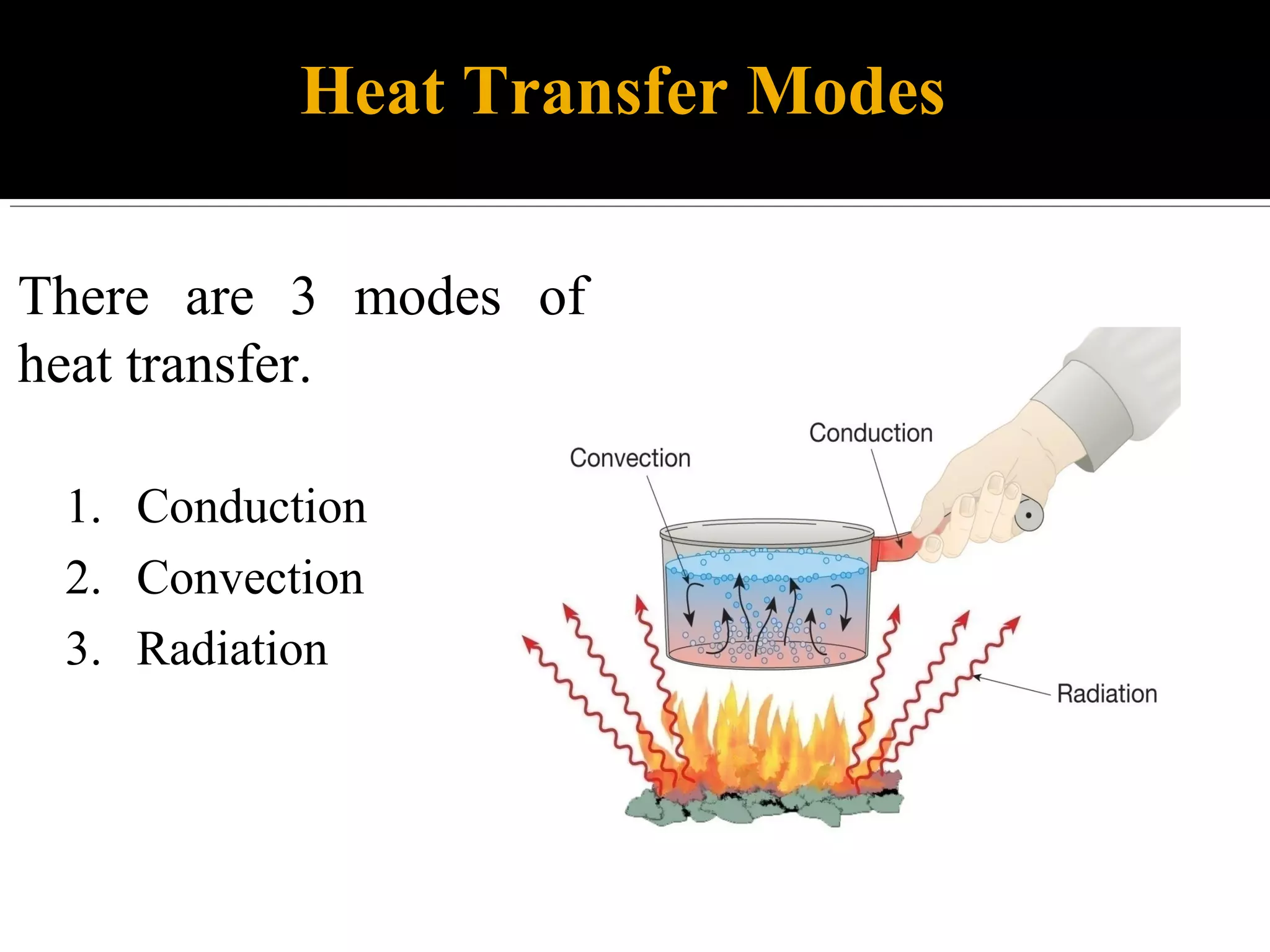
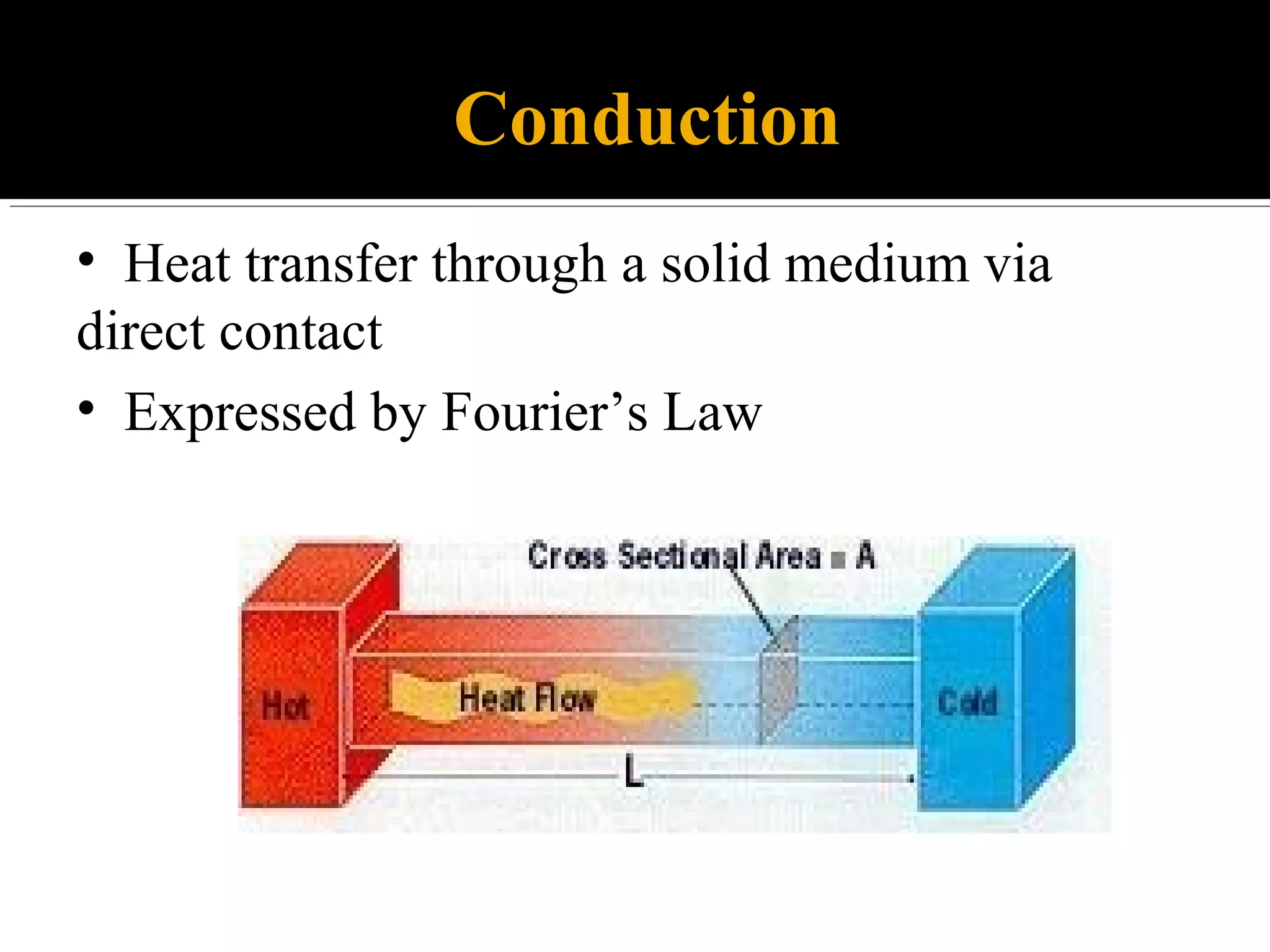
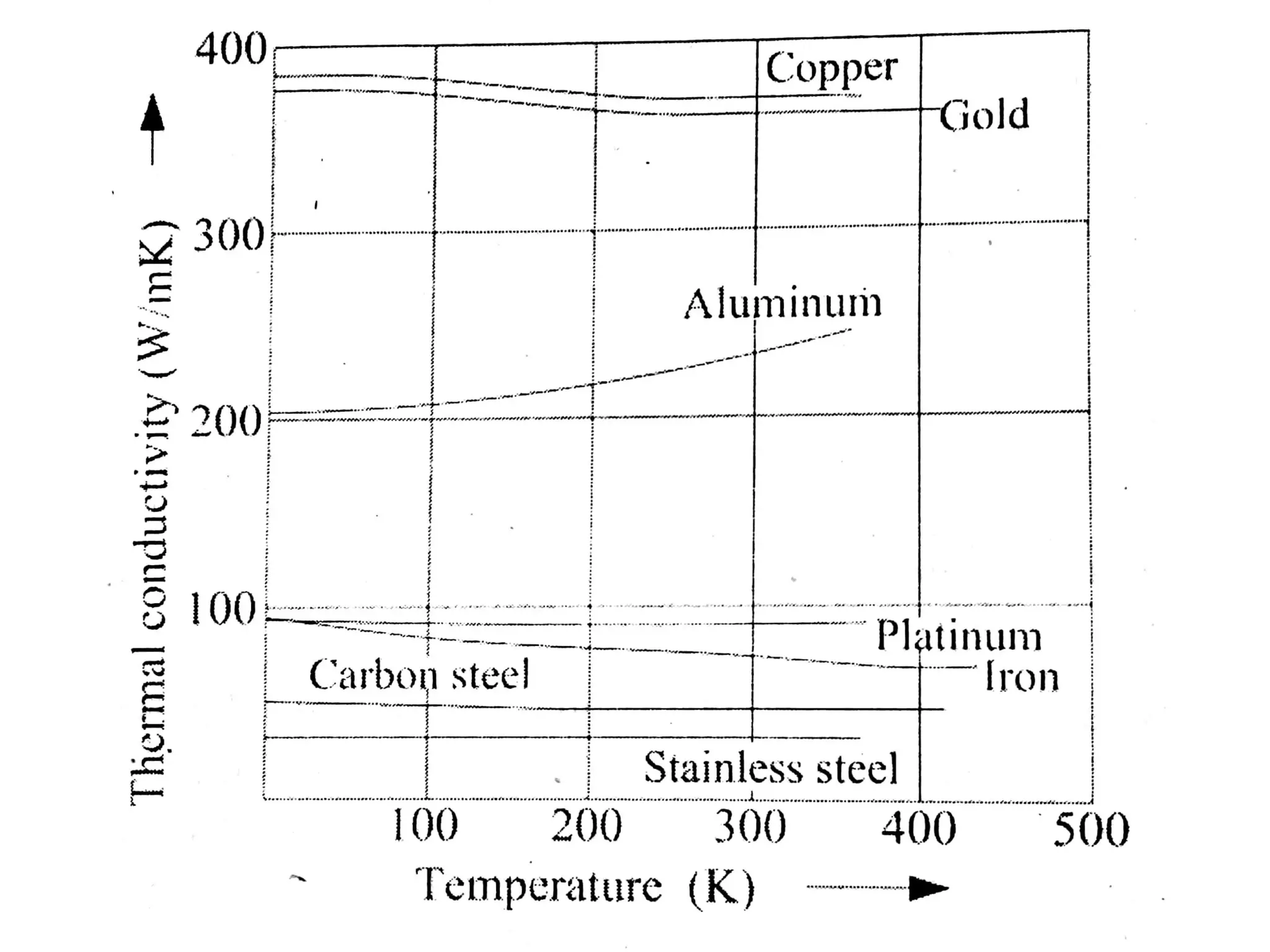
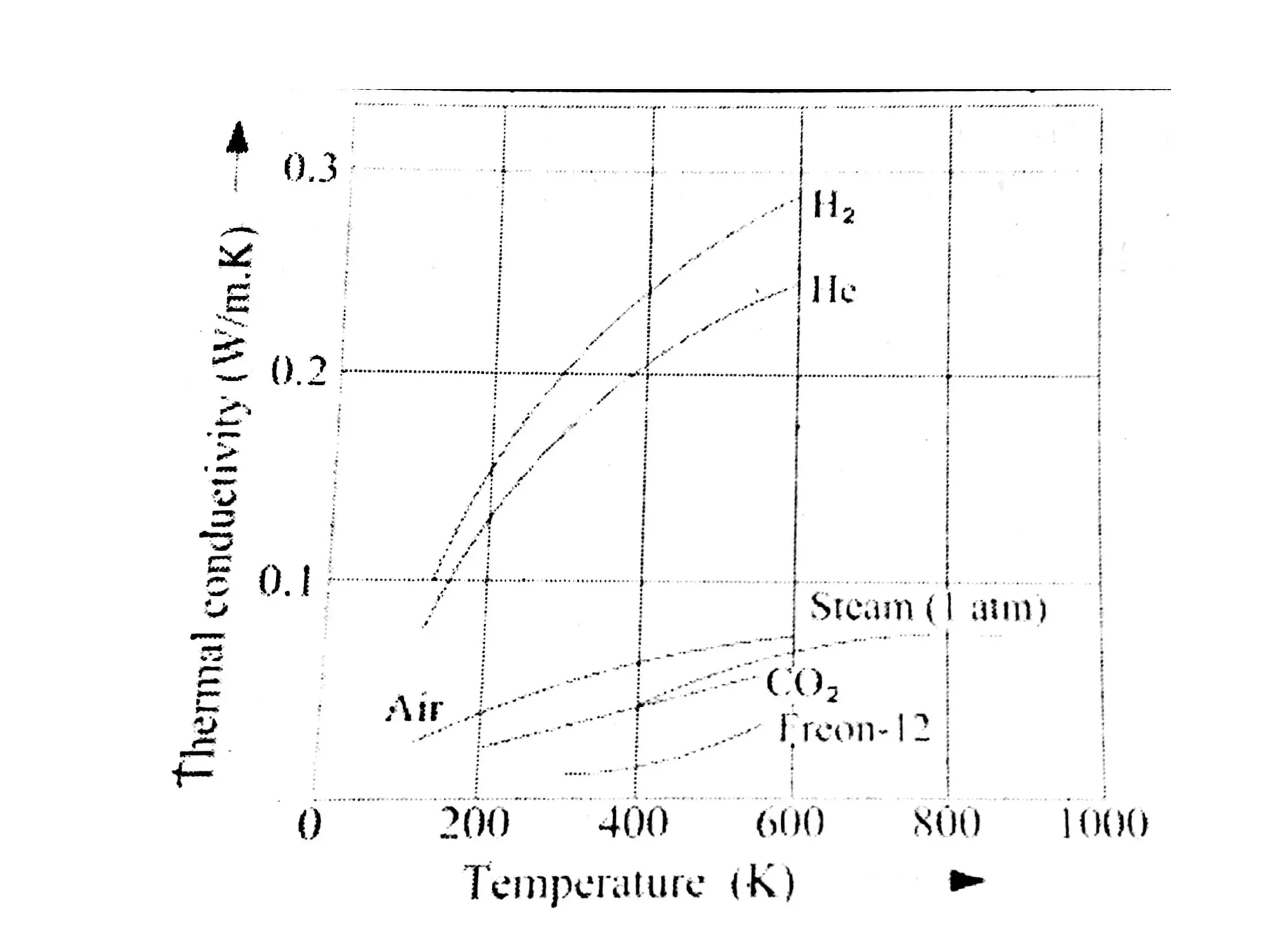
This document discusses heat transfer and conduction. It describes the three main modes of heat transfer as conduction, convection, and radiation. Conduction involves direct contact between solids, convection involves the movement of fluids, and radiation involves the transfer of heat through electromagnetic waves without a medium. The document also derives the generalized heat conduction equation for analyzing heat transfer in cylindrical coordinates.

1. Heat Transfer (2151903)
Mechanical Department
Sem.: 5th
D (D2)
• Prepared By: Sajan Gohel (160123119010)

2.  Modes of heat transfer
 Effect of temperature on thermal conductivity of
different solids, liquids and gases.
 Derivation of generalized equation in cylindrical

3. Heat Transfer Modes
There are 3 modes of
heat transfer.
1. Conduction
2. Convection
3. Radiation

4. Conduction
• Heat transfer through a solid medium via
direct contact
• Expressed by Fourier’s Law

5. Convection
• Convection is the transfer of heat
from one place to another by the
movement of fluids.
• Two kinds of convection
• Forced convection: Fluid is
forced
• Natural or free convection: fluid is
induced by temperature difference

6.  Radiation is the transfer of heat from the body or
fluid for which no medium.
 Heat transfer due to emission of electromagnetic
waves is known as thermal radiation

7.  Thermals conductivity of pure metals is due to
migration of three electrons (Kc) and lattice
vibrations (Kl).
K = Ke + Kl
 In pure metals, heat is transferred due to movement
of free electron in clouds and also due to vibrational
energy in lattice structure.
 Thermal conductivity of pure metal is decreases
with the increasing in temperature.

9.  Thermal conductivity of gases is smaller then that
of solids because there intermolecular spacing is
much larger.
 The thermal conductivity of all the gases increases
with increases with increases in temperature.
 This is because at high temperature collision among
gas particles increases and heat transfer increases.
K = 0.006 to 0.05 W/mK
K tα∆
K tα∆

11.  Heat conduction in liquids is also same as in gases.
 In case of liquids, close spacing of molecules and
strong molecular attraction force compare to gases
cause more heat exchange via collision.
 So the thermal conductivity of liquids usually lies
between those of gases and solids.
 In most of the liquids value of thermal conductivity
tends to decrease with increase in temperature.

13.  Consider an element
volume having the
coordinates (r, , z), for
three dimension heat
conduction analysis.
Volume of cylinder =
r * d * dr * dz
φ
φ
φ
K = thermal cunductivity
C = specific heat
P = density

14. • Net heat accumulated in the cylinder due to
conduction of heat.
 Heat flow in (x - ) plane.
Heat influx, Q’r =
Heat efflux, Q’(r+dr) =
Heat accomodation in the cylinder in radial direction,
 Heat flow in (r - z) plane.
Heat influx,
Heat efflux,
φ
'r (Qr)drQ
r
∂
+
∂
' (dr )
T
Q k dz dt
r
φ
φ
∂
= −
∂
'( ) ' (Q' )rdQ d Q
r
φ φ φ φ φ
φ
∂
+ = +
∂
2
2
1
dQ'r ( * * )( )dt
T T
k dr rd dz
r r r
φ
∂ ∂
= +
∂ ∂
( )
T
k rd dz dt
r
φ
∂
−
∂

15.  Heat accomodation in the cylinder in tengential
direction,
Heat influx Q’z=
Heat efflux Q(z+dz)=
Heat accomodation in the cylinder in axial
direction,
2
2 2
1
dQ' ( * * )( ) dt
T
k dr rd dz
r
φ φ
φ
∂
=
∂
Heat flow in (r - ) plane.φ
( )
T
k rd dr dt
z
φ
∂
−
∂
'z (Q, z) dzQ
r
∂
+
∂
2 2 2
2 2 2 2
1 1
dQ'z ( * * )( )dt
T T T T
k dr rd dz
r r r r z
φ
φ
∂ ∂ ∂ ∂
= + + +
∂ ∂ ∂ ∂

16.  Heat generated within the element
total heat generated
 Energy stored in element
 From eq. , A+B=C
' ( * * * )*B Q g qg dr r d dz dtφ= = =
* * * ( * * * )* * *
* * *
T
C dr r d dz dr r d dz c dt
t
dr rd dz dt
ρ φ φ
φ
∂
=
∂
( * * * )* * *
T
C dr r d dz c dt
t
ρ φ
∂
=
∂

17.  Dividing both sides by
we have ...
This eq. Is known as general heat conduction eq.
* * *dr rd dz dtφ
1
* *
c T T
k t t
ρ
α
∂ ∂
=
∂ ∂