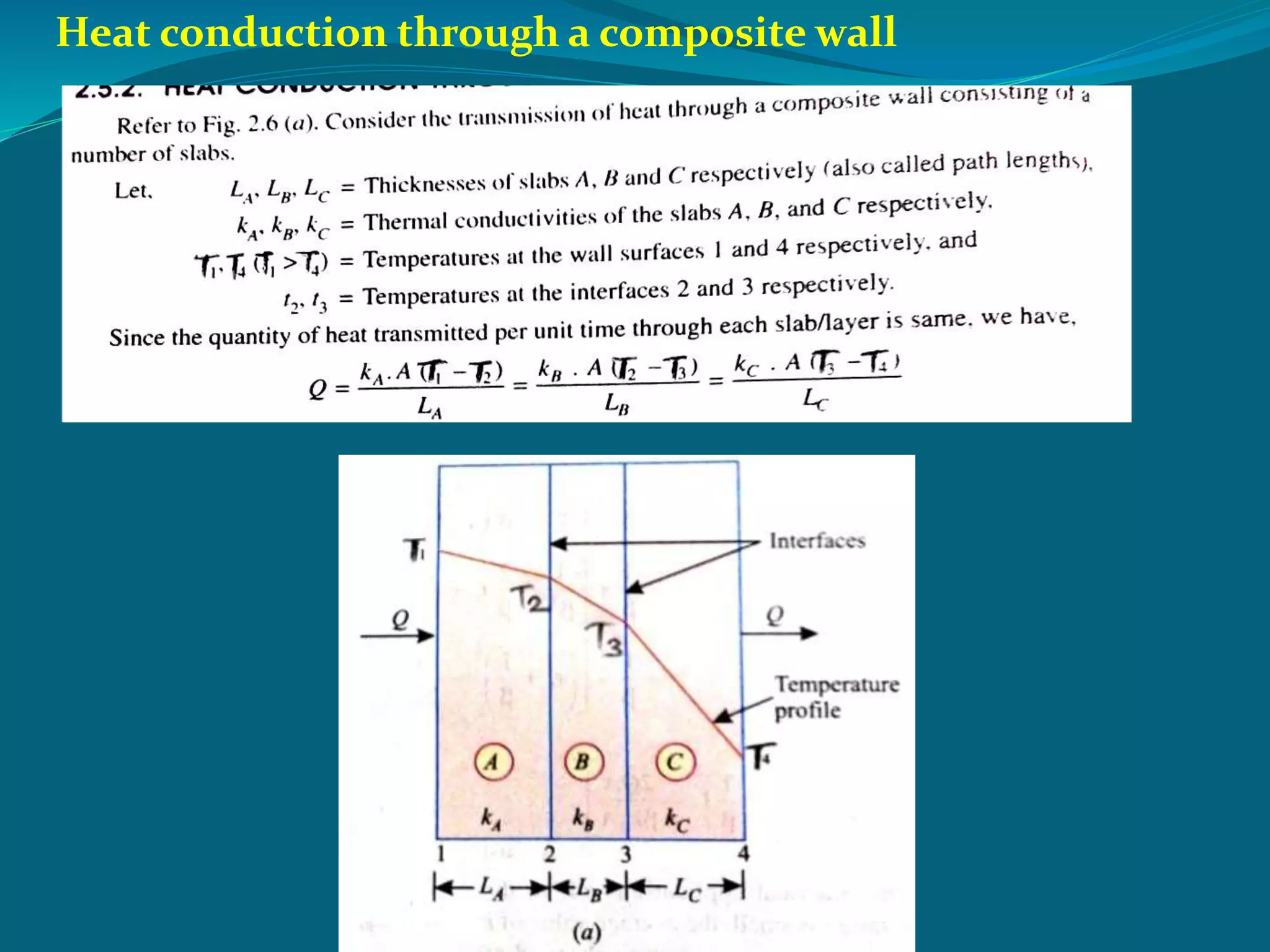
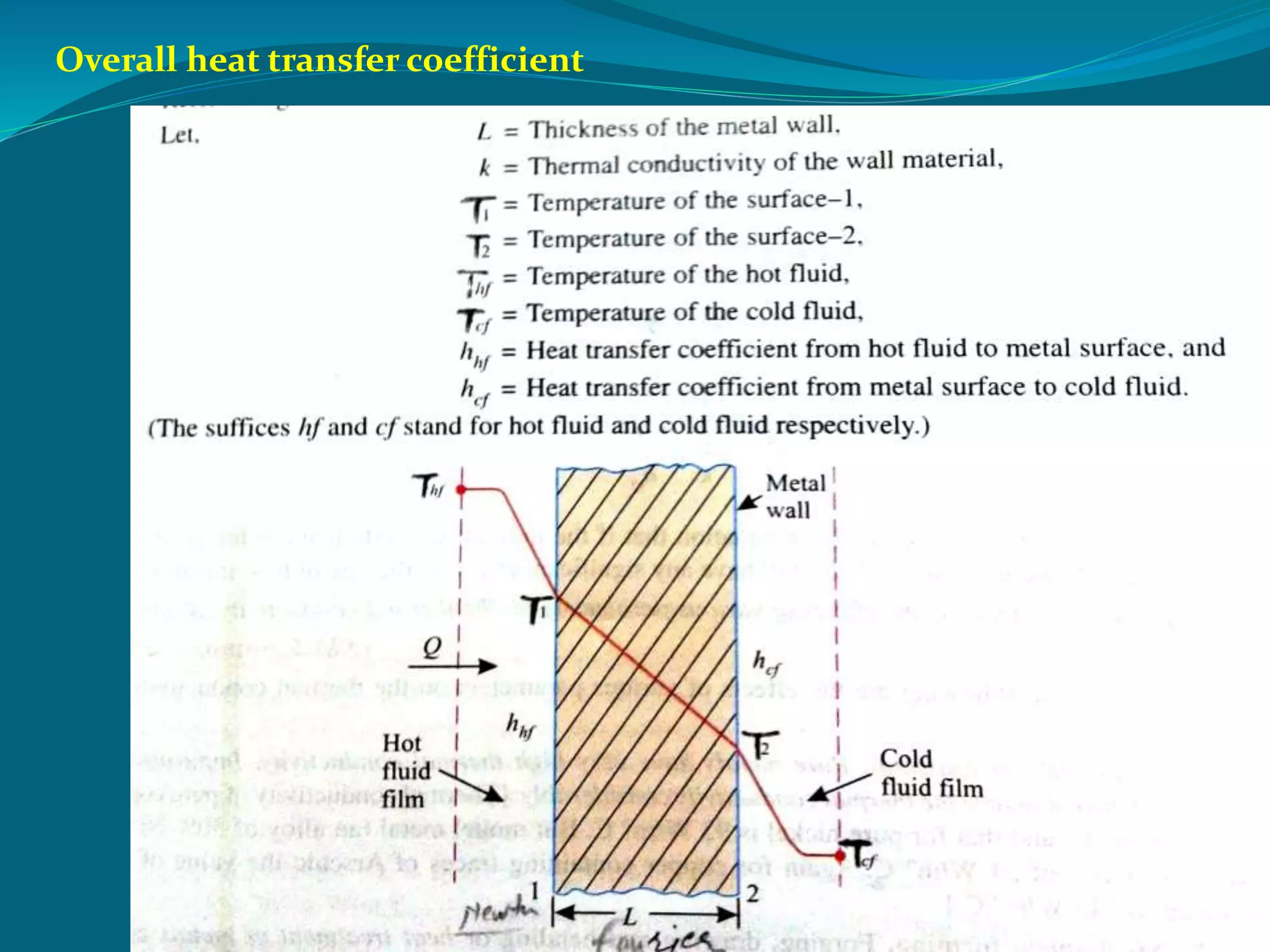
This document discusses heat conduction and the differential equation of heat conduction. It introduces the concept of using a differential element to model heat transfer in the x, y, and z directions. The rate of heat conduction into and out of the element is equated to the rate of heat generation and change in internal energy of the element to derive the general heat conduction equation. The document also discusses thermal diffusivity and its relationship to thermal conductivity and heat capacity, as well as heat conduction through composite walls.

1. HEAT CONDUCTION
PREAPARED
BY
ASHA KUMAWAT

2. DIFFERENTIAL EQUATION OF HEAT CONDUCTION
Differential element of dimensions dx- dy-dz
differential element in Cartesian co-ordinate system

3. From Fourier law,
1.Heat conducted into differential element in X-direction

4. 2. Heat conducted out of the differential element in X-
direction From the fundamental principle of
differentiation, we get

5. Substituting the value of dqx we get
Net amount of heat conducted in X-direction= dqx- dqx+dx
Similarly for Y and Z directions, we can write

6. Therefore net amount of heat conducted into the
differential element per unit time in all directions, is given
by
q be the rate of heat of generated per unit volume
The amount of heat generated in the differential element per unit
time
Where V-volume of element =dx.dy.dz

7. •The energy contained by the body is termed as internal energy.
•The flow of heat as well as generation of energy will result in
change in internal energy
•The rate of change of internal energy of the element per unit
volume is given by

8. Now balance for the differential element as
Rate of heat conduction into the element + rate of heat
generation in the element=rate of change of internal energy of
the element
Substituting the corresponding values and simplifying we get

10. Thermal diffusivity
It indicates the case at which energy gets diffused in the
volume of the substance. It is define as the ratio of thermal
conductivity to the heat capacity of a substance. It is given
by

13. By substituting above assumptions in the heat conducting equation we get

16. Heat conduction through a composite wall

18. Thermal conduction
resistance (L/KA)

19. Thermal contact resistance

20. Overall heat transfer coefficient

21. iv
v

22. vi