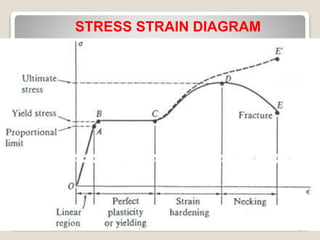
This document provides an overview of stress, strain, and modulus of elasticity concepts in mechanical engineering. It defines stress as force per unit area, strain as the deformation per original length. Hooke's law states deformation is directly proportional to force. The modulus of elasticity E is the constant of proportionality between stress and strain. A stress-strain diagram is presented showing the elastic region, yield point, plastic region, strain hardening, and necking behavior. Shear stress and modulus of rigidity G are also defined. Design considerations like factor of safety are discussed for selecting allowable loads below ultimate strengths.

1. Active Learning Assignment
(Mechanics of Solid )(2131903)
Topic:- Stress Strain and Basic concept
Mechanical Engineering (3 C3)
Prepared By:
Chandresh Suthar (140120119229)
Sonani Mananv (140120119229)
Govind Tade (140120119230)
Shah Shrey (140120119211)
Guided by:
Prof. Hiren Raghu

2. Flow of content
 Basic concept of stress & strain
 Direct Strain
 Module of elasticity
 Stress strain diagram
 Shear stress
 Module of rigidity

3. Stress and strain
DIRECT STRESS
 When a force is applied to an elastic body, the body deforms.
The way in which the body deforms depends upon the type of
force applied to it.
Compression force makes the body shorter.
A tensile force makes the body longer


4. A
F
Area
Force
Stress
2
/mN
Tensile and compressive forces are called DIRECT FORCES
Stress is the force per unit area upon which it acts.
….. Unit is Pascal (Pa) or
Note: Most of engineering fields used kPa, MPa, GPa.
( Simbol – Sigma)

5. 
L
x
Strain 
DIRECT STRAIN ,
In each case, a force F produces a deformation x. In engineering, we u
sually change this force into stress and the deformation into strain and
we define these as follows:
Strain is the deformation per unit of the original length.
The
symbol
Strain has no unit’s since it is a ratio of length to length. Most engineeri
ng materials do not stretch very mush before they become damages, s
o strain values are very small figures. It is quite normal to change small
numbers in to the exponent for 10-6( micro strain).
called EPSILON

6. MODULUS OF ELASTICITY (E)
•Elastic materials always spring back into shape when released. The
y also obey HOOKE’s LAW.
•This is the law of spring which states that deformation is directly prop
ortional to the force. F/x = stiffness = kN/m
•The stiffness is different for the different material and different sizes of the
material. We may eliminate the size by using stress and strain instead of f
orce and deformation:
•If F and x is refer to the direct stress and strain , then
AF  Lx 
L
A
x
F






Ax
FL
hence and

7. E 


Ax
FL
•The stiffness is now in terms of stress and strain only and this consta
nt is called the MODULUS of ELASTICITY (E)
• A graph of stress against strain will be straight line with gra
dient of E. The units of E are the same as the unit of stress.
ULTIMATE TENSILE STRESS
•If a material is stretched until it breaks, the tensile stress has reac
hed the absolute limit and this stress level is called the ultimate ten
sile stress.

8. STRESS STRAIN DIAGRAM

9. STRESS STRAIN DIAGRAM
Elastic behaviour
The curve is straight line trough out most of the region
Stress is proportional with strain
Material to be linearly elastic
Proportional limit
The upper limit to linear line
The material still respond elastically
The curve tend to bend and flatten out
Elastic limit
Upon reaching this point, if load is remove, the sp
ecimen still return to original shape

10. STRESS STRAIN DIAGRAM
Yielding
 A Slight increase in stress above the elastic limit will r
esult in breakdown of the material and cause it to defor
m permanently.
This behaviour is called yielding
The stress that cause = YIELD STRESS@YIELD POI
NT
Plastic deformation
Once yield point is reached, the specimen will elongat
e (Strain) without any increase in load
Material in this state = perfectly plastic

11. STRESS STRAIN DIAGRAM
 STRAIN HARDENING
 When yielding has ended, further load applied, resulting in a curve tha
t rises continuously
 Become flat when reached ULTIMATE STRESS
 The rise in the curve = STRAIN HARDENING
 While specimen is elongating, its cross sectional will decrease
 The decrease is fairly uniform
 NECKING
 At the ultimate stress, the cross sectional area begins its localised regi
on of specimen
 it is caused by slip planes formed within material
 Actual strain produced by shear strain
 As a result, “neck” tend to form
 Smaller area can only carry lesser load, hence curve donward
 Specimen break at FRACTURE STRESS

12. SHEAR STRESS
•Shear force is a force applied sideways on the material (transvers
ely loaded).
When a pair of shears cut a material
When a material is punched
When a beam has a transverse load

13. Shear stress is the force per unit area carrying the
load. This means the cross sectional area of the ma
terial being cut, the beam and pin.
A
F
 and symbol is called Tau•Shear stress,
The sign convention for shear force and stress is base
d on how it shears the materials as shown below.

14. 
L
x

L
x

SHEAR STRAIN
The force causes the material to deform as shown. The shear strain i
s defined as the ratio of the distance deformed to the height
. Since this is a very small angle , we can say that :
( symbol called
Gamma)
Shear strain

15. •If we conduct an experiment and measure x for various values of F,
we would find that if the material is elastic, it behave like spring and
so long as we do not damage the material by using too big force, th
e graph of F and x is straight line as shown.
MODULUS OF RIGIDITY (G)
The gradient of the graph is constant so tcons
x
F
tan
and this is the spring stiffness of the block in N/m.
•If we divide F by area A and x by the height L, the relationship is st
ill a constant and we get

16. tcon
Ax
FL
x
L
x
A
F
L
x
A
F
tan

A
F
Where
L
x

tcon
Ax
FL
x
L
x
A
F
tan

then
•If we divide F by area A and x by the height L, the relationship is st
ill a constant and we get
This constant will have a special value for each elastic material
and is called the Modulus of Rigidity (G).
G



17. ULTIMATE SHEAR STRESS
If a material is sheared beyond a certain limit and it becomes pe
rmanently distorted and does not spring all the way back to its ori
ginal shape, the elastic limit has been exceeded.
If the material stressed to the limit so that it parts into two, the ul
timate limit has been reached.
The ultimate shear stress has symbol and this value is used
to calculate the force needed by shears and punches.


18. DOUBLE SHEAR
Consider a pin joint with a support on both ends as shown. This
is called CLEVIS and CLEVIS PIN
 By balance of force, the force in the two supports is F/2 each
The area sheared is twice the cross section of the pin
So it takes twice as much force to break the pin as for a case of
single shear
Double shear arrangements doubles the maximum force allowe
d in the pin

19. LOAD AND STRESS LIMIT
DESIGN CONSIDERATION
Will help engineers with their important task in Designing structur
al/machine that is SAFE and ECONOMICALLY perform for a spec
ified function
DETERMINATION OF ULTIMATE STRENGTH
An important element to be considered by a designer is how the
material that has been selected will behave under a load
This is determined by performing specific test (e.g. Tensile test)
ULTIMATE FORCE (PU)= The largest force that may be applied t
o the specimen is reached, and the specimen either breaks or beg
ins to carry less load
ULTIMATE NORMAL STRESS
(U) = ULTIMATE FORCE(PU) /AREA

20. ALLOWABLE LOAD / ALLOWABLE STRESS
Max load that a structural member/machine component will be allowed t
o carry under normal conditions of utilisation is considerably smaller than
the ultimate load
This smaller load = Allowable load / Working load / Design load
Only a fraction of ultimate load capacity of the member is utilised when
allowable load is applied
The remaining portion of the load-carrying capacity of the member is ke
pt in reserve to assure its safe performance
The ratio of the ultimate load/allowable load is used to define FACTOR
OF SAFETY
FACTOR OF SAFETY = ULTIMATE LOAD/ALLOWABLE LOAD
@
FACTOR OF SAFETY = ULTIMATE STRESS/ALLOWABLE STRESS

21. SELECTION OF F.S.
1. Variations that may occur in the properties of the member under consi
derations
2. The number of loading that may be expected during the life of the stru
ctural/machine
3. The type of loading that are planned for in the design, or that may occ
ur in the future
4. The type of failure that may occur
5. Uncertainty due to the methods of analysis
6. Deterioration that may occur in the future because of poor maintenan
ce / because of unpreventable natural causes
7. The importance of a given member to the integrity of the whole struct
ure

22. AXIAL FORCE & DEFLECTION OF BODY
Deformations of members under axial loading
If the resulting axial stress does not exceed the proportional limit of
the material, Hooke’s Law may be applied
Then deformation (x / ) can be written as
AE
FL

 E