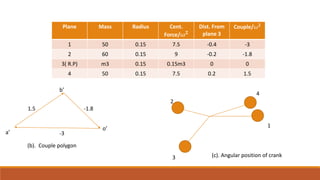
This document discusses balancing of reciprocating masses in inline multi-cylinder engines. It explains that inline engines have inner and outer cranks that cause unbalanced primary and secondary forces and couples. The conditions for complete primary and secondary balancing are presented, requiring balancing of forces and couples. Analytical methods are provided for primary and secondary balancing calculations. As an example, a four cylinder engine is analyzed to find the third cylinder's mass and angular position needed for primary balance based on the given masses and positions of the other cylinders.

1. GANDHINAGAR INSTITUTE OF TECHNOLOGY
Dynamics Of Machine (2161901)
Active Learning Assignment
On
Dynamics of Reciprocating Masses
Branch : Mechanical Engineering
Batch : 6 C-3
Prepared by: Guided By:
Suthar Chandresh (140120119229) Prof. Samir Raval

2. Content
 Introduction
 Condition for Complete balancing
 Primary Balancing of inline Multi-cylinder Engines
 Secondary Balancing of inline multi-cylinder Engines
 Balancing of four cylinder inline engines

3. Introduction
 Reciprocating parts of any machine is subjected to continuous acceleration and retardation.
 Inertia acted opposite to the acceleration of part.
 This inertia force is disturbing or unbalanced dynamic force acting on reciprocating part.
 Eliminate the unbalanced force by using suitable balancing masses.
 The balancing of reciprocating masses is divided into :
• Balancing reciprocating masses in single cylinder engine
• Balancing reciprocating masses in multi cylinder inline engine
• Balancing reciprocating masses in V-engine

4. Balancing reciprocating masses in
Multi-cylinder inline engine
The multi-cylinder engine having the axes of all the engine of all the cylinders in the same plane and on
the same side of the axis of the crank shaft, are known as inline engine.
In the multi-cylinder engines unbalanced force and couples are acting.
The multi-cylinder engine have two inner crank and two outer crank.
For the inner crank angle = θ˚
For the outer crank angle =180+ θ˚
The unbalanced forces due to reciprocating mass of each
Cylinder are ;[Primary force , Fp= mω 𝟐r cos θ ] [secondary force= mω 𝟐r{
cos 2θ
𝒏
}

5. Condition for complete balancing
Primary balancing
 Primary forces must be balanced.
∑mω2r cosθ= 0
 Primary couple must be balanced.
∑mω2
r l cosθ= 0
Secondary balancing
 Secondary forces must be balanced.
∑ mω 𝟐r{
cos 2θ
𝒏
}
 Secondary couple must be balanced.
∑ mω 𝟐
rl{
cos 2θ
𝒏
}

6. Analytical method for primary balancing
For complete primary balancing, the analytical solution is;
∑ mr cosθ= 0 ∑mr sinθ= 0
∑ mrl cosθ= 0 ∑ mrl sinθ= 0
Analytical method for secondary balancing
∑
mr
𝑛
cos 2θ= 0 ∑
mr
𝑛
sin 2θ= 0
∑
mrl
𝑛
cos 2θ= 0 ∑
mrl
𝑛
sin 2θ= 0

7. EXAMPLE : A four cylinder vertical engine has crank 150 mm long . The planes of rotation of first ,
second and fourth crank are 400 mm, 200 mm and 200mm respectively from the third crank and their
reciprocating mases are 50kg, 60kg and 50 kg respectively. Find the mass of the third reciprocating part
and their relative angular position of the cranks in order that the engine may be in complete primary
balance.
Sol.:- Given , r1 = r2 = r3 = r4 = 150 mm = 0.15m ; m1 = 50 kg, m2 = 60 kg, m4 = 50 kg ;
In order to give the primary balance of the reciprocating parts of a multi-cylinder engine, the
problem may be treated as that of revolving masses
with the reciprocating masses transferred to their respective crank pins.
1 2 3 4
-ve R.P +ve
200 mm 200 mm
400mm
(a) Position of plane

8. Plane Mass Radius Cent.
Force/ω 𝟐
Dist. From
plane 3
Couple/ω 𝟐
1 50 0.15 7.5 -0.4 -3
2 60 0.15 9 -0.2 -1.8
3( R.P) m3 0.15 0.15m3 0 0
4 50 0.15 7.5 0.2 1.5
a’
b’
o’
-1.81.5
-3
(b). Couple polygon
1
2
3
4
(c). Angular position of crank

9. By measurement we find the angle between crank 2 and crank 1 is 160˚ in anticlockwise.
θ2 = 160˚
And angle between crank 4 and crank 1 is 26˚ in anticlockwise.
θ4 = 26˚
In order to find the mass of the third cylinder (m3) and its angular position, draw the force
polygon, to some suitable scale.
7.5
9
7.5
0.15m3 From the fig. , 0.15 m3 = 9 kg-m
m3 = 60 kg.
and θ3 = 227 ˚