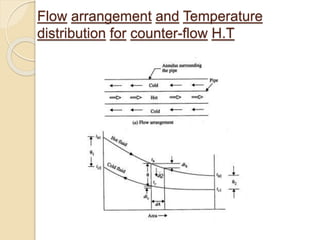
1) The document discusses counter-flow heat exchangers and defines the logarithmic mean temperature difference (LMTD) for calculating heat transfer in counter-flow exchangers. 2) It then defines effectiveness as the ratio of actual heat transfer to maximum possible heat transfer and derives an equation for effectiveness in terms of the number of transfer units (NTU) and heat capacity ratio (R). 3) An example problem is then presented to calculate the mass flow rate of cooling water, effectiveness, and required heat exchange area for a given counter-flow exchanger problem.

1. :-

2. Flow arrangement and Temperature
distribution for counter-flow H.T

3. Logarithmic Mean Temperature
Difference (LMTD) for Counter-Flow
Considering an elementary area dA of the heat exchanger.
The rate of flow of heat through this elementary area is given
by :-
Deriving this we get,
Where, θm=LMTD
θ1 = th1
− tc2
θ2 = th2
− tc1
dQ = U ⋅ dA(th − tc) = U ⋅ dA ⋅ Δt …….(i)
Q =
)UA(θ2 − θ1
)ln(θ2 θ1
Since, Q=U ⋅ A ⋅ θm
∴ θm =
θ2 − θ1
)ln(θ2 θ1

4. Effectiveness :-
The heat exchange dQ through an area dA of the heat
exchanger is given by ,
…….(ii)
From expression (ii),we get,
Substituting the value of dQ from expression (i) and
rearranging the equation, we get,
d(th − tc) = −U ⋅ dA(th − tc)
1
Ch
−
1
Cc
dQ = −m
•
hCph
dth = m
•
cCpc
dtc
= −Chdth = Ccdtc
dth =
−dQ
Ch
and dtc =
dQ
Cc
or d(th − tc) = −dQ
1
Ch
−
1
Cc

5. d(th − tc)
(th − tc)
= − U ⋅ dA
1
Ch
−
1
Cc
ln
(th2−tc1)
(th1−tc2)
= −U ⋅ A
1
Ch
−
1
Cc
∴ ln
(th2−tc1)
(th1−tc2)
=
UA
CC
1 −
Cc
Ch
∴
(th2
− tc1
)
(th1
− tc2
)
= exp
UA
CC
1 −
Cc
Ch
Now, From effectiveness equation,
ε=
Q
⋅
Qmax
=
Actual H.T
Max possible H.T
ε =
Ch(th1
− th2
Cmin(th1
− tc1
=
Cc(tc2
− tc1
Cmin(th1
− tc1
∴ 𝑡ℎ2
= 𝑡ℎ1
−
𝜀𝐶min(𝑡ℎ1
− 𝑡 𝑐1
𝐶ℎ

6. ∴ tc2
=
εCmin(th1
− tc1
Cc
+ tc1
Substituting the values of tc2
and th2
, we get
Since,Cmin Cmax=R and UA/Cmin=NTU
ε =
1 − exp −NTU(1 − R)
1 − Rexp −NTU(1 − R)
ε =
1 − exp (−U A Cmin) 1 − Cmin Cmax
1 −
Cmin
Cmax
exp (−U A Cmin) 1 − Cmin Cmax

7. Here, we find that effectiveness of parallel flow and counter-
flow .
ε =
1−exp −NTU(1−R)
1−Rexp − NTU(1−R)
…..Counter flow
ε =
1−exp −NTU(1+R)
1+R
…….(parallel flow)

8. Example:- A Counter-flow heat exchangeris used to cool
0.55 kg/sec with Cp=2.45kJ/kg˚C of Oil from 115˚C to
40˚C by the use of water. The inlet and outlet temp. of
cooling water are 15˚C and 75˚C respectively. The
Overall heat transfer coefficient is 1450W/m2˚C.
Using NTU method, Calculate the following :
1)The mass flow rate of water
2)The effectiveness of Heat exchanger
3)The Surface area required.
Given Data :- th1
= 115˚C , th2
= 40˚C ,
tc1
= 15˚C , tc2
= 75˚C ,
U= 1450W/m2˚C,
mh= 0.55 kg/sec ,
Cph
=2.45kJ/kg˚C ,
Cpc
(water)=4.187kJ/kg˚C

9. i) Q=mCp Δt
∴ m
•
hCph
(th1
− th2
) = m
•
cCpc
(tc2
− tc1
)
∴ 0.55 × 2.45 115 − 40 = m
•
c×4.187(75-15)
∴ m
•
c= 0.40 kg/sec
ii) Ch = m
•
hCph
Cc = m
•
cCpc
=2.45×0.55 =4.187×0.40
=1.3475 =1.6748
Here, Ch<Cc
∴ Cmin = Ch=1.3475
ε =
Ch(th1−th2
Cmin(th1−tc1
=
)1.3475(115−40
)1.3475(115−15
∴ ε = 0.75

10. iii) Heat capacity ratio, R =
Cmin
Cmax
=
1.3475
1.6748
= 0.81
ε =
1 − exp −NTU(1 − R)
1 − Rexp − NTU(1 − R)
∴ 0.75 =
1 − exp −NTU(1 − 0.81)
1 − 0.81exp − NTU(1 − 0.81)
∴ NTU = 2.4736
∴ 2.4736 =
1450 × A
1.3475
NTU =
UA
Cmin
∴ A = 2.2987 m2