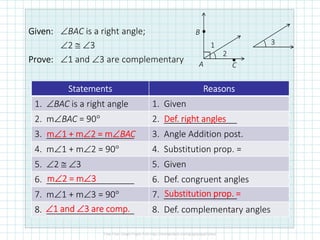
Geometry proofs follow a deductive structure with undefined terms, postulates, definitions, and theorems. A proof justifies statements using these elements through a series of statements and reasons. For example, if angle A is a right angle, then its measure is 90 degrees by the definition of a right angle. Proofs also use properties like the transitive property of equality and congruence. The last statement of a proof should be what is being proved, not "Prove."

1. Geometric Proofs
Objectives
The student is able to (I can):
• Set up simple proofs

2. Geometry is based on a deductive structure—a system of
thought in which conclusions are justified by means of
previously assumed or proved statements. Every deductive
structure contains the following four elements:
• Undefined terms (points, lines, planes)
• Assumptions known as postulates
• Definitions
• Theorems and other conclusions• Theorems and other conclusions
A deductive system is very much like a game—to play, you
have to learn the terms being used (definitions) and the rules
(postulates).

3. An argument, a justification, or a reason that something is
true. To write a proof, you must be able to justify statements
using properties, postulates, or definitions.
Example: Name the property, postulate, or definition that
justifies each statement.
StatementStatementStatementStatement JustificationJustificationJustificationJustificationStatementStatementStatementStatement JustificationJustificationJustificationJustification
If ∠A is a right angle, then
m∠A = 90°.
Definition of a right angle
If ∠2 ≅ ∠1 and ∠1 ≅ ∠5,
then ∠2 ≅ ∠5
Transitive property
m∠ABD+m∠DBC=m∠ABC Angle Addition Post.
If B is the midpoint of ,
then AB = BC.
Definition of midpointAC

4. Line segments with equal lengths are congruent, and angles
with equal measures are also congruent. Therefore, the
reflexive, symmetric, and transitive properties of equality
have corresponding properties of congruenceproperties of congruenceproperties of congruenceproperties of congruence.
Reflexive Property of Congruence
fig. A ≅ fig. A
Symmetric Property of CongruenceSymmetric Property of Congruence
If fig. A ≅ fig. B, then fig. B ≅ fig. A.
Transitive Property of Congruence
If fig. A ≅ fig. B and fig. B ≅ fig. C, then fig. A ≅ fig. C.

5. Example:
Given:Given:Given:Given: AM bisects
Prove:Prove:Prove:Prove:
CD
CM MD≅
•
D
M
C
•
A
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
1. bisects 1. Given
2. 2. Def. of midpoint
AM CD
CD MD≅
While the first reason is almost always “Given”, the
last reason is nevernevernevernever “Prove”. In fact, “Prove” is nevernevernevernever
everevereverever used as a reason in a proof (NEVERNEVERNEVERNEVER)....
The last statement of your proof should always be
what you are trying to prove.
2. 2. Def. of midpointCD MD≅

6. Example:
Given:Given:Given:Given: p ⊥ r
Prove:Prove:Prove:Prove: ∠1 and ∠2 are complementary
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
p
r
1
2
•
S
•
T
•
A
•P
1. p ⊥ r 1. Given
2. m∠PAT = 90° 2. Def. of perpendicular
3. m∠PAT = m∠1 + m∠2 3. Angle Addition Post.
4. m∠1 + m∠2 = 90° 4. Substitution prop. =
5. ∠1 and ∠2 are comp. 5. Def. of complementary angles

7. Example:
Given:Given:Given:Given: NA = LE
N is midpoint of
L is midpoint of
Prove:Prove:Prove:Prove:
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
•
E
L
G
N
A
GA
GE
GN GL≅
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
1. NA = LE
N is midpoint of
L is midpoint of
1. Given
2. 2. Def. of midpoint
3. 3. Def. of congruent segments
4. 4. Substitution prop. ≅
5. 5. Substitution prop. ≅
;GN NA GL LE≅ ≅
NA LE≅
GN LE≅
GA
GE
GN GL≅

8. GivenGivenGivenGiven:::: ∠BAC is a right angle;
∠2 ≅ ∠3
ProveProveProveProve:::: ∠1 and ∠3 are complementary
1
2
3
•
•
B
A C
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
1. ∠BAC is a right angle 1. Given
2. m∠BAC = 90° 2. _______________2. m∠BAC = 90° 2. _______________
3. __________________ 3. Angle Addition post.
4. m∠1 + m∠2 = 90° 4. Substitution prop. =
5. ∠2 ≅ ∠3 5. Given
6. __________________ 6. Def. congruent angles
7. m∠1 + m∠3 = 90° 7. _______________
8. __________________ 8. Def. complementary angles

9. GivenGivenGivenGiven:::: ∠BAC is a right angle;
∠2 ≅ ∠3
ProveProveProveProve:::: ∠1 and ∠3 are complementary
1
2
3
•
•
B
A C
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
1. ∠BAC is a right angle 1. Given
2. m∠BAC = 90° 2. _______________Def. rightDef. rightDef. rightDef. right anglesanglesanglesangles2. m∠BAC = 90° 2. _______________
3. __________________ 3. Angle Addition post.
4. m∠1 + m∠2 = 90° 4. Substitution prop. =
5. ∠2 ≅ ∠3 5. Given
6. __________________ 6. Def. congruent angles
7. m∠1 + m∠3 = 90° 7. _______________
8. __________________ 8. Def. complementary angles
Def. rightDef. rightDef. rightDef. right anglesanglesanglesangles
mmmm∠∠∠∠1 + m1 + m1 + m1 + m∠∠∠∠2 = m2 = m2 = m2 = m∠∠∠∠BACBACBACBAC
SubstitutionSubstitutionSubstitutionSubstitution prop. =prop. =prop. =prop. =
mmmm∠∠∠∠2 = m2 = m2 = m2 = m∠∠∠∠3333
∠∠∠∠1 and1 and1 and1 and ∠∠∠∠3 are comp.3 are comp.3 are comp.3 are comp.