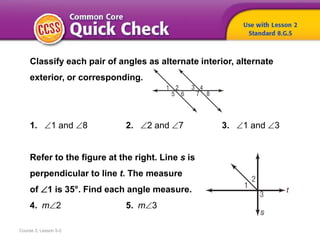
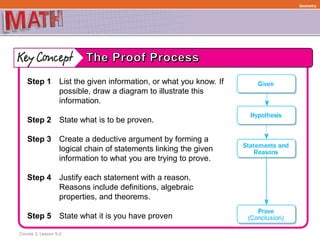
The document discusses paragraph proofs and two-column proofs in geometry. A paragraph proof states the given information, what is to be proven, then uses a logical chain of statements and reasons to justify the conclusion. A two-column proof separates the statements from the reasons into two columns, with the given information and conclusion stated. Both proof styles use definitions, properties, and theorems to logically justify each step. The document provides examples of each type of proof to illustrate the process.

1. Classify each pair of angles as alternate interior, alternate
exterior, or corresponding.
1. 1 and 8 2. 2 and 7 3. 1 and 3
Refer to the figure at the right. Line s is
perpendicular to line t. The measure
of 1 is 35°. Find each angle measure.
4. m2 5. m3
Course 3, Lesson 5-2

2. Course 3, Lesson 5-2
ANSWERS
1. alternate exterior
2. alternate interior
3. corresponding
4. 55°
5. 90°

3. HOW can algebraic concepts be
applied to geometry?
Geometry
Course 3, Lesson 5-2

4. Course 3, Lesson 5-2 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Geometry
• Preparation for 8.G.6
Explain a proof of the Pythagorean Theorem and its converse.
Mathematical Practices
1 Make sense of problems and persevere in solving them.
2 Reason abstractly and quantitatively.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.

5. To prove a conjecture
• using a paragraph proof,
• using a two-column proof
Course 3, Lesson 5-2
Geometry

6. • inductive reasoning
• deductive reasoning
• proof
• paragraph proof
• informal proof
• two-column proof
• formal proof
• theorem
Course 3, Lesson 5-2
Geometry

7. Course 3, Lesson 5-2
Geometry
Step 1 List the given information, or what you know. If
possible, draw a diagram to illustrate this
information.
Step 2 State what is to be proven.
Step 3 Create a deductive argument by forming a
logical chain of statements linking the given
information to what you are trying to prove.
Step 4 Justify each statement with a reason.
Reasons include definitions, algebraic
properties, and theorems.
Step 5 State what it is you have proven

8. 1
Need Another Example?
2
3
Step-by-Step Example
1. The diamondback
rattlesnake has a
diamond pattern on its
back. An enlargement
of the skin is shown.
If m∠1 = m∠4, write a
paragraph proof to show
that m∠2 = m∠3.
Given: m∠1 = m∠4
Proof:
Prove: m∠2 = m∠3
m∠1 = m∠2 because they are vertical angles. Since m∠1 = m∠4,
m∠2 = m∠4 by substitution. m∠4 = m∠3 because they are vertical
angles. Since m∠2 = m∠4, then m∠2 = m∠3 also by substitution.
Therefore, m∠2 = m∠3.

9. Answer
Need Another Example?
Refer to the diagram. If
m∠1 = m∠5, write a paragraph
proof to show that m∠1 = m∠11.
m∠1 = m∠9 because they are corresponding
angles. m∠9 = m∠11 because they are vertical
angles. Since m∠9 = m∠11, then m∠1 = m∠11
by substitution.

10. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. Write a two-column proof to show that if two
angles are vertical angles, then they have the
same measure.
Statements
lines m and n intersect;
∠1 and ∠3 are vertical angles.
Given: lines m and n intersect; ∠1 and ∠3 are vertical angles
Prove: m∠1 = m∠3
Reasons
a. Given
∠1 and ∠2 are a linear pair
and ∠3 and ∠2 are a linear pair.
b. Definition of linear pair
m∠1 + m∠2 = 180º
m∠3 + m∠2 = 180º
c. Definition of supplementary angles
m∠1 + m∠2 = m∠3 + m∠2d. Substitution
5 m∠1 = m∠3 Subtraction Property of Equalitye.

11. Answer
Need Another Example?
Write a two-column proof to show that if
PQ = QS and QS = ST, then PQ = ST.
Given: PQ = QS; QS = ST
Prove: PQ = ST
Statements
PQ = QS and QS = ST
Reasons
a. Given
PQ = STb. Substitution

12. How did what you learned
today help you answer the
HOW can algebraic concepts be applied
to geometry?
Course 3, Lesson 5-2
Geometry

13. How did what you learned
today help you answer the
HOW can algebraic concepts be applied
to geometry?
Course 3, Lesson 5-2
Geometry
Sample answers:
• When completing a two-column proof, you may define
a variable and write equations as part of the
statements.
• When completing a two-column proof, you use some
properties of equality for reasons.

14. Describe the differences
between a paragraph proof
and a two-column proof.
Ratios and Proportional RelationshipsFunctionsGeometry
Course 3, Lesson 5-2