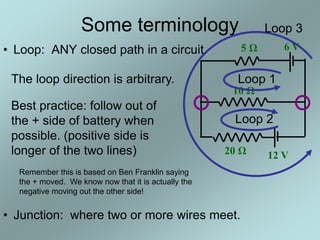
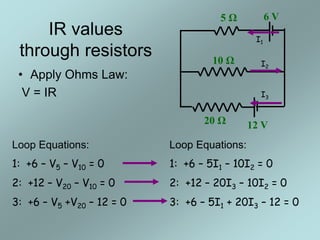
1) Kirchoff's rules were developed by Gustav Kirchoff in the 1800s to solve complex circuits. 2) Kirchoff's junction rule states that the sum of all currents entering a junction must equal the sum of all currents leaving the junction. 3) Kirchoff's loop rule states that the sum of the changes in potential around any closed loop in a circuit must be zero.

1. Kirchoff’s Rules
Purpose: solve
complex circuits
Gustav Robert Kirchoff
German physicist
1800’s
Konigsber, Prussia.

2. Some terminology
• Loop: ANY closed path in a circuit. 5 Ω 6 V
10 Ω
12 V20 Ω
• Junction: where two or more wires meet.
Best practice: follow out of
the + side of battery when
possible. (positive side is
longer of the two lines)
The loop direction is arbitrary. Loop 1
Loop 2
Loop 3
Remember this is based on Ben Franklin saying
the + moved. We know now that it is actually the
negative moving out the other side!

3. 5 Ω 6 V
10 Ω
12 V20 Ω
1. Junction Rule (Conservation of Charge)
• At any junction the sum of all currents
entering must equal the sum of all currents
leaving the junction.
Remember the junctions!
You choose current directions.
Remember “Out of +, Into –”
when possible.
Each junction must have at least 1
current coming and 1 current
leaving.
I1
I3
I2
Phet Simulation
Kirchoff Circuit.cck
Junction Equations:
I1 + I3 = I2

4. 5 Ω 6 V
10 Ω
12 V20 Ω
2. Loop Rule (Conservation of Energy)
• The sum of the changes in potential
(voltage) around any closed path of a
circuit must be zero.
Loop 1
Voltage: + or – ???
Start your loop with the battery.
Battery (gives energy)
V is + when your loop goes
out of +, into – (uphill)
Resistor (takes energy)
V is – when your loop and
current are in the same
directions (downhill)
Loop Equations:
1: +6 – V5 – V10 = 0
2: +12 – V20 – V10 = 0
3: +6 – V5 +V20 – 12 = 0
I1
I3
I2
Loop 2
Loop 3

5. 5 Ω 6 V
10 Ω
12 V20 Ω
IR values
through resistors
• Apply Ohms Law:
V = IR
Loop Equations:
1: +6 – V5 – V10 = 0
2: +12 – V20 – V10 = 0
3: +6 – V5 +V20 – 12 = 0
Loop Equations:
1: +6 – 5I1 – 10I2 = 0
2: +12 – 20I3 – 10I2 = 0
3: +6 – 5I1 + 20I3 – 12 = 0
I1
I3
I2

6. Now solve for the currents!
Simplify and Solve.
I1 + I3 = I2
+6 – 5I1 +20I3 – 12 = 0
+12 – 20I3 – 10I2 = 0
+6 – 5I1 – 10I2 = 0
5I1 - 20I3 = -6
10I2 + 20I3 = 12
5I1 +10I2 = 6
Combine these 2 eq.
5I1 +10(I1 + I3) = 6
5I1 + 10I1 + 10I3 = 6
15I1 + 10I3 = 6
I1 = (6 – 10I3)/15
5(6 – 10I3)/15 - 20I3 = -6
6 – 10I3 - 60I3 = -18
-70I3 = -24
I3 = 0.343 A

7. The rest is easy!
I1 + I3 = I2
5I1 - 20I3 = -6
10I2 + 20I3 = 12
5I1 +10I2 = 6
I3 = 0.343 A
5I1 – 20(0.343) = -6
I1 = 0.172 A
10I2 + 20(0.343) = 12
I2 = 0.514 A
Double Check.
I1 + I3 = I2
0.172 + 0.343 = 0.514
0.515 ≈ 0.514