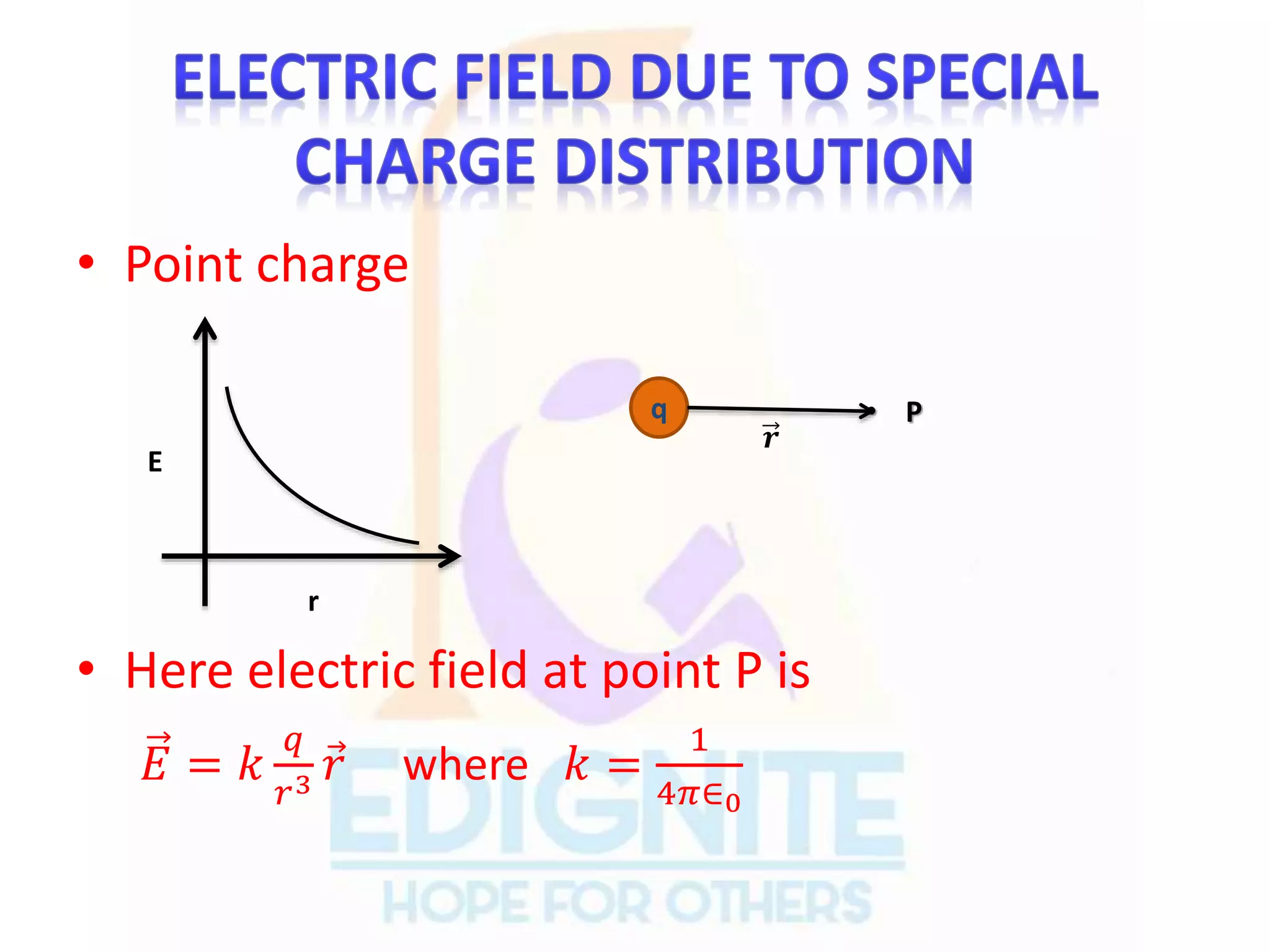
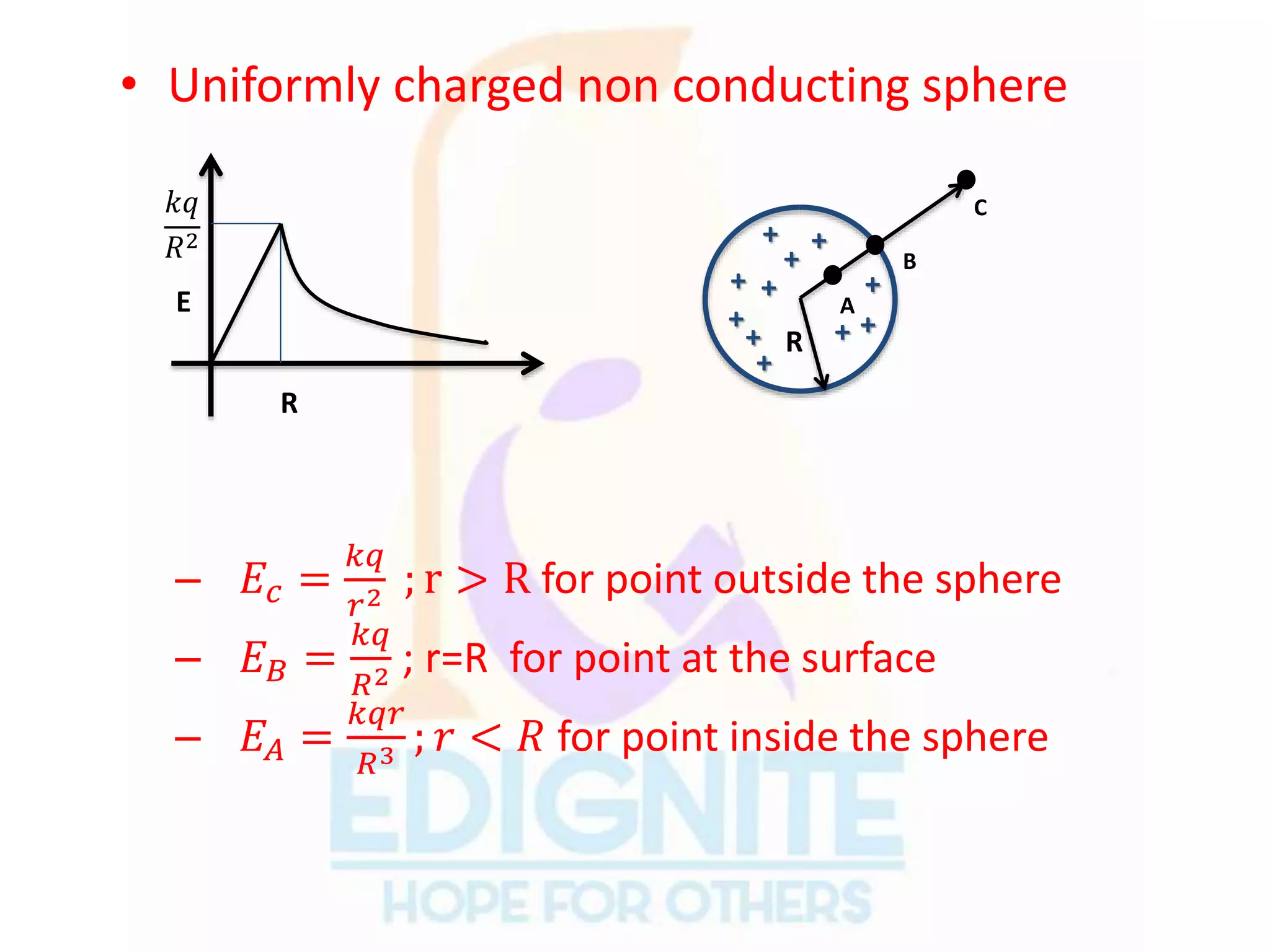
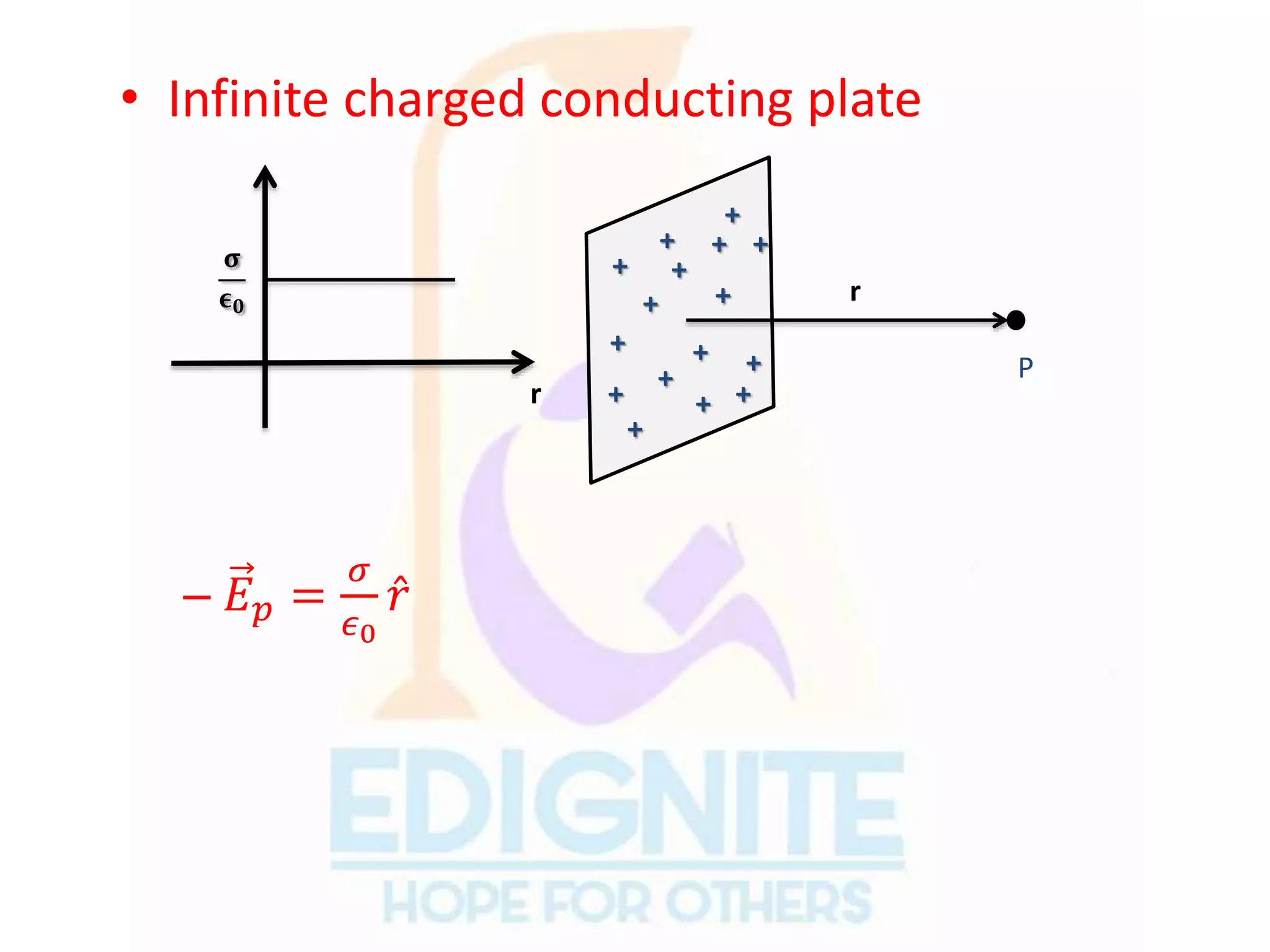
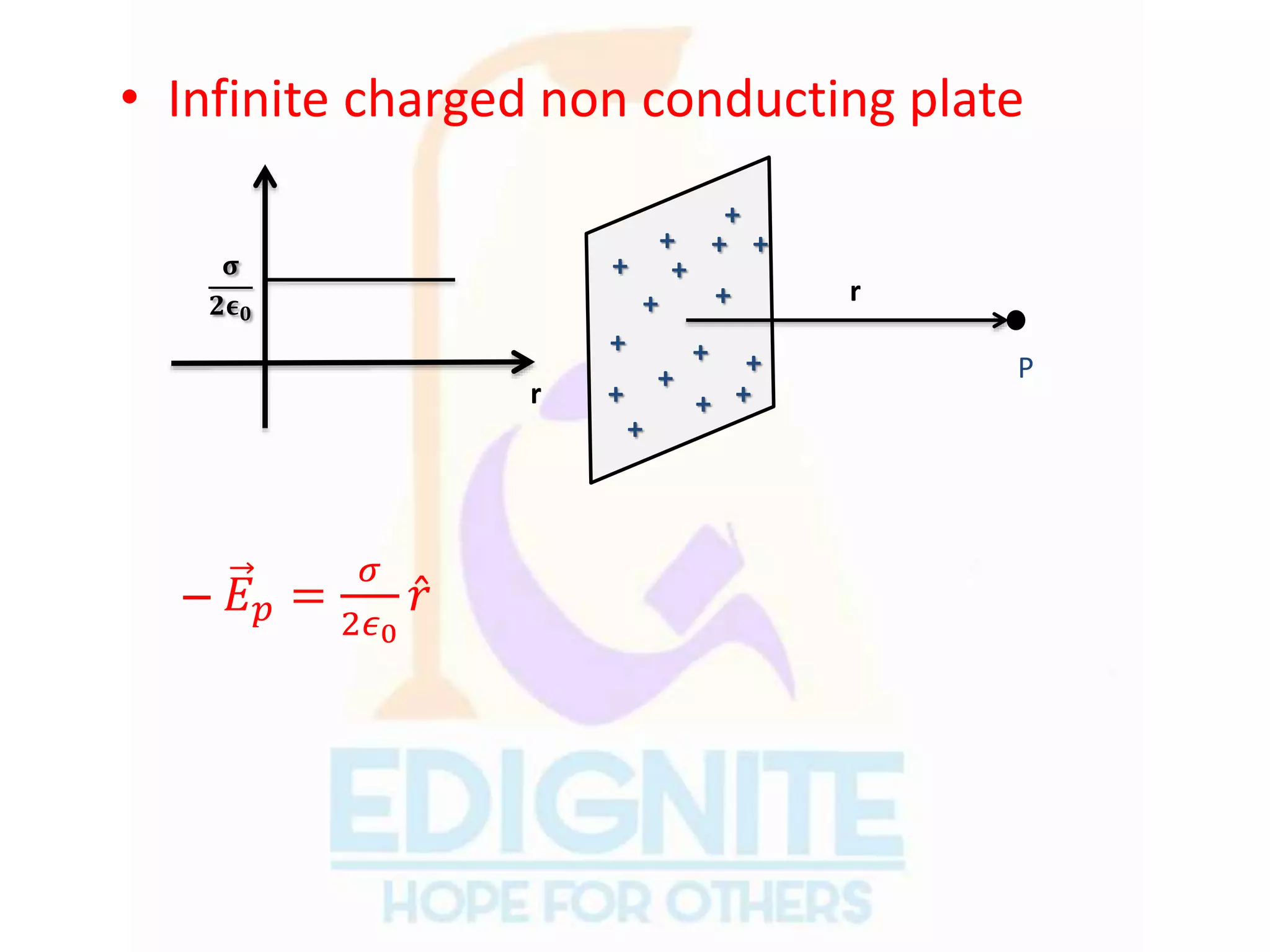
The document covers essential concepts related to electric charges and fields, including the types of charges, units of charge, conservation of charge, and Coulomb's law, which describes the force between point charges. It also explains electric fields, electric dipoles, electric flux, and Gauss's law, along with the behavior of electric fields due to various charge distributions. Key principles such as the superposition of forces and the characteristics of electric field lines are also discussed.

1. Electric charges and fields
Basic concepts

2. • Charge of a material body is that property due
to which it interacts with other charges.
• There are two kinds of charges :- positive and
negative charge.
• S.I. unit of charge is coulomb and is denoted
by C.

3. • Additivity of charges:- The total charge of a system is equal
to the algebraic sum of all the charges that the system
consists of, i.e., if the system consists of 𝑞1, 𝑞2, 𝑞3 ⋯ 𝑞 𝑛,
then the total charge of the system is 𝑞1 + 𝑞2 + 𝑞3 ⋯ 𝑞 𝑛.
• Quantization of Charge:- It has been established that all
free charges are basic unit of charge denoted by e. Thus
any charge q, on the body is 𝑞 = 𝑛𝑒; where n is any integer
and the value of e is 1.6 × 10−19
𝐶.
• Conservation of charge:-The total charge of an isolated
system is always conserved. It is neither created nor
destroyed.

4. • According to Coulomb’s Law:-
The force between two point charges is directly proportional to
product of two charges and is inversely proportional to the square
of distance between them.
𝑭 = 𝒌
𝒒 𝟏 𝒒 𝟐
𝒓 𝟐
Where 𝒌 =
𝟏
𝟒𝝅𝝐 𝟎
Here ∈0 is permitivity of the vaccum. Its value in SI units is 8.854 ×
10−12 𝐶2 𝑁−1 𝑚−2
• In vector form, the force can be written as
• 𝑭 𝟏𝟐 =
𝟏
𝟒𝝅𝝐 𝟎
𝒒 𝟏 𝒒 𝟐
𝒓 𝟐 𝒓 𝟏𝟐
𝒒 𝟏 𝒒 𝟐r
𝒒 𝟐𝒒 𝟏
𝒓 𝟏𝟐

5. • Force on any charge due to a number of other
charges is a vector sum of all forces on that
charge due to other charges, taken one at a time.
The individual forces are unaffected due to the
presence of other charges. This is termed as
principle of supereposition.
• So according to principle of superposition if
𝐹1, 𝐹2, 𝐹3 ⋯ 𝐹𝑛 are the forces on a charge q due to
charges 𝑞1, 𝑞2, 𝑞3 ⋯ 𝑞 𝑛 respectively, then the net
force on charge q is
𝐹 = 𝐹1 + 𝐹2 + 𝐹3+ ⋯ 𝐹𝑛

6. • The electric field due to a charge Q is the region
in the space where any other charge experiences
force of attraction or repulsion due to the charge
Q. Here charge q is called the source charge and
the charge which experiences the electrostatic
force, say q, is called the test charge.
• Electric field intensity – The electric field
intensity or the strength of electric field is the
force experienced by a unit positive charge
placed in an electric field generated by a single
charge Q or a group of charges.

7. • As electric field is the force on unit positive
charge, it is a vector quantity.
• Now let the electric fields due to charges
𝑞1, 𝑞2 ⋯ 𝑞 𝑛 be 𝐸1, 𝐸2, 𝐸3, ⋯ 𝐸 𝑛, respectively.
• Then the net electric field
𝐸 = 𝐸1+ 𝐸2 +⋯ 𝐸 𝑛

8. • Electric field lines are a way of representing electric field
pictorially
• They are curves in an electric field such that tangent to any
curve at any point would give direction of electric field at
that point.
• The magnitude of electric field at any point is now directly
proportional to the density of field lines at that point.
• Electric field lines for a charge q

9. • Field lines start from positive charges and end at
negative charges. If there is a single charge, they may
start or end at infinity.
• In a charge- free region, electric field lines can be taken
to be continuous curves without any breaks.
• Two field lines can never cross each other. (If they did,
the field at the point of intersection will not have a
unique direction, which is absurd.)
• Electrostatic field lines do not form any closed loops.
This follows from the conservative nature of the
electric field.

10. • Electric flux is the measure of relative amount
of electric field lines passing through a surface
area.
• Mathematically the electric flux ∆𝜑 through a
surface ∆𝑆 is ∆𝜑 = 𝐸 ∙ ∆𝑆 = 𝐸∆𝑆 cos 𝜃
E
∆𝑆
𝜃

11. • The electric dipole is the system of two charges of
equal magnitude and opposite nature separated
by a finite distance.
• For example the system of charges q and –q
separated by a distance 2a is known as an electric
dipole with magnitude dipole moment p = qx2a
and direction along the electric field line
emerging from -q charge to q charge.
• The dipole moment 𝑝 = (𝑞 × 2𝑎) 𝑟
q -q
𝒓
2a

12. • Case I:- When the point is on the axis of the dipole.
• 𝐸 𝑞 =
1
4𝜋𝜖0
𝑞
𝑟−𝑎 2 (𝑖)
• Also 𝐸−𝑞 =
1
4𝜋𝜖0
−𝑞
𝑟+𝑎 2 (𝑖𝑖)
• Now net electric field 𝐸 = 𝐸 𝑞 + 𝐸−𝑞 =
1
4𝜋𝜖0
𝑞
𝑟−𝑎 2 −
1
4𝜋𝜖0
𝑞
𝑟+𝑎 2 =
𝑞
4𝜋𝜖0
4𝑎𝑟
𝑟2−𝑎2 2
• Now as a<<r (as the distance is very large), 𝑟2
− 𝑎2
~ 𝑟2
• Thus 𝐸 =
2𝑘 𝑝
𝑟3
q -q
2ar
1 C

13. • Case II:- When the point is at the equatorial point of the
dipole.
• 𝐸 𝑞 =
1
4𝜋𝜖0
𝑞
𝑟2+𝑎2 (𝑖)
• Also 𝐸−𝑞 =
1
4𝜋𝜖0
𝑞
𝑟2+𝑎2 (𝑖𝑖)
• Now net electric field 𝐸 = 𝐸 𝑞 + 𝐸−𝑞 = −
2𝑞𝑎
4𝜋𝜖0 𝑟2+𝑎2
3
2
𝑝
• Now as a<<r (as the distance is very large), 𝑟2
− 𝑎2
~ 𝑟2
• Thus 𝐸 =
−𝑘 𝑝
𝑟3
1 C
2a
p
r
𝑬
𝐸−𝑞
𝐸 𝑞
q
-q

14. • When the dipole is making an angle θ with the
electric field:-
• Here, as we can see from the figure that the
net force cancels out.
• The dipole thus experiences a
couple (torque) of magnitude
𝜏 = 𝑞𝐸 × 2𝑎 sin 𝜃 = 2𝑞𝑎 𝐸 𝑠𝑖𝑛𝜃
Thus in vector form, it can be written as 𝜏 = 𝑝 × 𝐸
θ
-qE
qE
-q
q
E
a

15. • According to Gauss’s law, the net electric flux through a closed
surface S is 1/∈0 times the charge enclosed by the surface.
• So net flux through a surface, 𝜑 =
𝑞
𝜖0
, where q is the total enclosed
charge within the surface.
• It is true for any closed surface, no matter what its shape or size is.
• The surface that we chose for the application of Gauss’s law is
called the Gaussian surface.
• The Gaussian surface cannot pass through any discrete charge. This
is because electric field due to system of discrete charges is not well
defined at the location of any charge (as the electric field tends to
infinity). However, the Gaussian surface can pass through a
continuous charge distribution.

16. • Field due to an infinitely long straight uniformly
charged wire.
• Here we need to find electric
field at a distance r from the center
• So assuming the cylindrical
Gaussian surface of radius r, we get
𝐸 ∙ 𝐴 =
𝑞
𝜖0
𝐸 × 2𝜋𝑟𝑙 = 𝜆 ×
𝑙
𝜖0
𝐸 =
𝜆
2𝜋𝜖0 𝑟
𝑛
r
l
E
+
+
+
+
+
+
+
+
+ Charge per
unit length=λ

17. • Field due to uniformly charged infinite plane
sheet.
• Here consider a parallelopiped
(whose two planes which are
parallel to the sheet are having
area A) passing through the infinite
sheet.
So 2𝐸 ∙ 𝐴 =
𝑞
𝜖0
=
𝜎𝐴
𝜖0
𝐸 =
𝜎
2∈0
+
+
+
+ +
+
+
+
+
+
+
x
Charge per unit area =σ
E
E
E

18. • Here we consider following cases:-
I. When the point is inside the
Shell. Here when we pass a spherical
gaussian surface through point A, we
can see That there is no enclosed
charge Inside it. Thus the net flux
through it is zero. Hence electric field
at any point inside the shell is zero.
II. When we need find electronic field at
any point C outside the spherical shell, we consider
a spherical surface passing through C and of radius r.
So, here 𝐸 ∙ 𝐴 =
𝑞
𝜖0
𝐸 × 4𝜋𝑟2
=
𝑞
𝜖0
𝐸 =
1
4𝜋∈0
𝑞
𝑟2
If r = R (radius of the sphere), 𝐸 =
1
4𝜋∈0
𝑞
𝑅2
A
B
C
R
+
+
++
+
+
+
+
+
+

19. • Point charge
• Here electric field at point P is
𝐸 = 𝑘
𝑞
𝑟3 𝑟 where 𝑘 =
1
4𝜋∈0
E
r
q
𝒓
• P

20. • Charged conducting sphere
– 𝐸𝑐 =
𝑘𝑞
𝑟2 ; r > R for point outside the sphere
– 𝐸 𝐵 =
𝑘𝑞
𝑅2 ; r=R for point at the surface
– 𝐸𝐴 = 0 ; 𝑟 < 𝑅 for point inside the sphere
E
R
𝑘𝑞
𝑅2
A
B
C
R
+
+
++
+
+
+
+
+ +

21. • Uniformly charged non conducting sphere
– 𝐸𝑐 =
𝑘𝑞
𝑟2 ; r > R for point outside the sphere
– 𝐸 𝐵 =
𝑘𝑞
𝑅2 ; r=R for point at the surface
– 𝐸𝐴 =
𝑘𝑞𝑟
𝑅3 ; 𝑟 < 𝑅 for point inside the sphere
E
R
𝑘𝑞
𝑅2
A
B
C
R
+
+
++
+
+
+ +
+
+ +

22. • Linear charge distribution of length l
– 𝐸 =
λ sin
𝑎+𝑏
2
2𝜋𝜖0 𝑟
=
2𝑘 λ sin
𝑎+𝑏
2
𝑟
𝑟;
λ = 𝑢𝑛𝑖𝑓𝑜𝑟𝑚 𝑐ℎ𝑎𝑟𝑔𝑒 𝑑𝑖𝑠𝑡𝑟𝑖𝑏𝑢𝑡𝑖𝑜𝑛 = 𝑞/𝑙
– When 𝑙 ∞ 𝐸 =
2𝑘𝜆
𝑟
𝑟
E
R
a
b
r
l
P
𝐸

23. • Charged circular ring at an axial point
– 𝐸 𝑝 =
𝑘𝑄𝑥
𝑅2+𝑥2
3
2
– The electric field is zero at the centre of the ring
and maximum at 𝑥 = ±
𝑅
2
𝑹
𝟐
x
R
P
+
+
+
+
+
+
+
+
+
+
+
+
r
𝐸
-
𝑹
𝟐
E

24. • Due to charged circular disk
– 𝐸 𝑝 =
𝜎
2𝜖0
1 −
𝑥
𝑅2+𝑥2
x
R
P
+
+
+
+ +
+
+
+
+
+
++
r
𝐸
E

25. • Infinite charged conducting plate
– 𝐸 𝑝 =
𝜎
𝜖0
𝑟
𝛔
𝛜 𝟎
r
P
+
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+
r

26. • Infinite charged non conducting plate
– 𝐸 𝑝 =
𝜎
2𝜖0
𝑟
𝛔
𝟐𝛜 𝟎
r
P
+
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+
r

27. • Electric charge
• Properties of charge
• Coulomb’s Law
• Superposition principle
• Electric field
• Electric field lines
• Electric flux
• Electric Dipole and electric field due to it at axial and equatorial
points.
• Torque on electric dipole due to an electric field
• Gauss law
• Application of Gauss law
• Electric field due to some special charge distribution