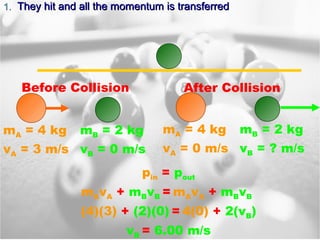
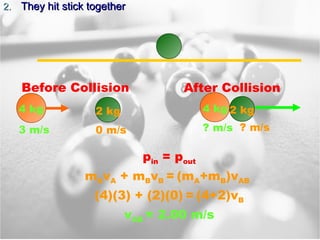
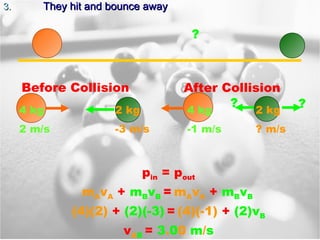
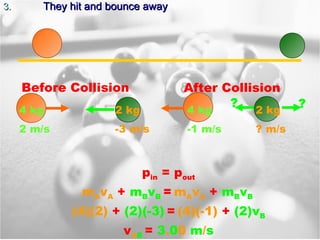
1) Momentum is defined as mass times velocity. Impulse is defined as the change in momentum over time caused by an applied force. 2) A rocket at rest experiences an impulse of 100,000 N-sec from thrusters applying an average force of 5,000 N over 20 seconds, giving the rocket a final velocity of 24.5 m/s. 3) The law of conservation of momentum states that momentum is never created or destroyed in a system. It remains constant in collisions whether objects stick together or bounce apart.

1. MomentumMomentum
Chapter 6Chapter 6

2. Momentum (Symbol = p) [Unit = kg m/s]
 Inertia in motion  The Quantity of Motion
Momentum = Mass • Velocity
p = m • v
Newton’s 2nd
Law
Impulse = change in momentum
( )
f i
f i
f i
v vvF ma a
t t
v v
t F m t
t
Ft mv mv
−∆= = =
−
• = •
= −
Impulse (Symbol = I)[Unit = Nsec]
 A force in a certain time
Concept: In order to change momentum,
we need a force in a certain amount of time!
f ipI Ft mv mv=∆= = −

3. f ipI Ft mv mv=∆= = −
Changing Momentum
Difference between hitting
concrete bridge vs. yellow barrels full of pea gravel
Seat belt vs. Air bag
Δp = Ft Δp = Ft
0 - m v = FT 0 - m v = Ft
http://www.regentsprep.org/Regents/physics/phys01/impulse/default.htm
Momentum is a vector, so direction is important!

4. A 4.0 x 104
N rocket is at rest when it fires its thrusters.
If the thrusters put out an average force of 5.0 x 103
N
over 20 sec, then
(a) What is the impulse the rocket experiences?
(b) What is the rocket’s final velocity?
(a) Impulse
I = F t
I = 5000 (20)
I = 100,000 Nsec
(b) v
I = ∆p = mvf – mvi
100,000 = 4080 vf – 4080(0)
vf = 24.5 m/s

6. Conservation of MomentumConservation of Momentum
Law of Conservation of MomentumLaw of Conservation of Momentum
 Momentum cannot be created or destroyedMomentum cannot be created or destroyed
Momentum In = Momentum outMomentum In = Momentum out
ppinin = p= poutout
2 Types of Collisions
Elastic  Energy is conserved
Inelastic  Energy is lost to heat, sound, etc.
Since we work in a happy, ideal world, we will deal with all elastic collisions.
This is for
Collisions!

7. 1.1. They hit and all the momentum is transferredThey hit and all the momentum is transferred
mA = 4 kg
vA = 3 m/s
mB = 2 kg
vB = 0 m/s
Before Collision
mA = 4 kg
vA = 0 m/s
mB = 2 kg
vB = ? m/s
After Collision
pin = pout
mAvA + mBvB = mAvA + mBvB
(4)(3) + (2)(0) = 4(0) + 2(vB)
vB = 6.00 m/s

8. 2.2. They hit stick togetherThey hit stick together
4 kg
3 m/s
2 kg
0 m/s
Before Collision
4 kg
? m/s
2 kg
? m/s
After Collision
pin = pout
mAvA + mBvB = (mA+mB)vAB
(4)(3) + (2)(0) = (4+2)vB
vAB = 2.00 m/s

9. 3.3. They hit and bounce awayThey hit and bounce away
4 kg
2 m/s
2 kg
-3 m/s
Before Collision
4 kg
-1 m/s
2 kg
? m/s
After Collision
pin = pout
mAvA + mBvB = mAvA + mBvB
(4)(2) + (2)(-3) = (4)(-1) + (2)vB
vAB = 3.00 m/s
? ?
?

10. 3.3. They hit and bounce awayThey hit and bounce away
Before Collision After Collision
pin = pout
mAvA + mBvB = mAvA + mBvB
(4)(2) + (2)(-3) = (4)(-1) + (2)vB
vAB = 3.00 m/s
4 kg
2 m/s
2 kg
-3 m/s
4 kg
-1 m/s
2 kg
? m/s
? ?

11. 4.4. Both start with zero velocityBoth start with zero velocity
4 kg
0 m/s
2 kg
0 m/s
Before Collision
4 kg
? m/s
2 kg
20 m/s
After Collision
pin = pout
mAvA + mBvB = mAvA + mBvB
(4)(0) + (2)(0) = (4)(vA) + (2)(20)
vA = -10.0m/s