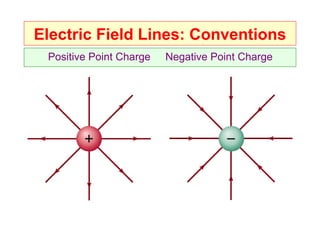
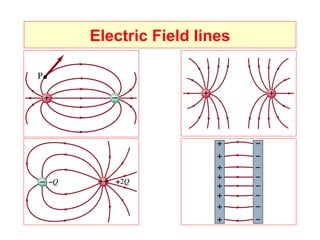
Electricity and magnetism are fundamentally linked phenomena that underpin modern technology. Electric forces exist between charged objects and atoms due to the interactions of positive protons in atomic nuclei and negative electrons orbiting them. Electricity controls many biological processes in living things. While objects are electrically neutral overall, applying forces can cause separations of charge that result in objects or parts of objects becoming electrically charged.

1. Electricity and Magnetism
 Electric forces hold atoms and
molecules together.
 Electricity controls our thinking, feeling,
muscles and metabolic processes.
 Electricity and magnetism underpin
much of our current technology (e.g.
computers).
 Electricity and magnetism are linked
on a fundamental level.

2. Electric Charges
• Evidence for electric charges is everywhere, e.g.
– static electricity.
– lightning.
• Objects may become charged by contact and
frictional forces.
• Benjamin Franklin (1700’s) discovered that there are
two types of charges:
– positive charge.
– negative charge.
• Franklin also discovered that like charges repel and
unlike charges attract one another.
• Electric charge is
– quantized (Millikan)
– conserved (Franklin)

3. Electric Charges in Atoms
• Atoms consist of a nucleus
containing positively
charged protons.
• The nucleus of an atom is
surrounded by an equal
number of negatively
charged electrons.
• The net charge on an atom
is zero.
• An atom may gain or lose
electrons, becoming an ion
with a net negative or
positive charge. Nuclear diameter ~ 10-15 m
(femtometer)
• Polar molecules have zero
net charge but their charges Atomic diameter ~ 10-9 m
are unevenly distributed in
space (e.g. water). (nanometer)

4. Classes of Materials
• CONDUCTORS are materials in which
charges may move freely (e.g. copper).
• INSULATORS are materials in which charges
cannot move freely (e.g. glass).
• SEMICONDUCTORS are materials in which
charges may move under some conditions
(e.g. silicon).

5. Charges and the Earth
• The earth acts as a near-infinite source
or sink of charges, and therefore its net
charge cannot easily be changed.
• Any conductor in contact with the earth
is said to be GROUNDED and cannot
receive a net charge. (principle of
lightning rod)

6. Induced Charge
• Charged objects brought close to a conductor may
cause charge to redistribute (polarize the conductor).
• If a polarized conductor is momentarily grounded,
charge will be transferred to/from the earth, and it
may be left with a net charge (by INDUCTION).
• Objects may be charged by
– conduction (requires contact with another
charged object.
– induction (requires no contact with another
charged object).

7. Electric Force and Coulomb’s Law
• If two point charges q1 and q2 are separated
by a distance r, the magnitude of the electric
force Fe between them is:
q1 q2
Fe = k 2
r
where k = 8.99 x 10 9 N m2/C2 is the Coulomb
constant, q1 and q2 are in Coulombs (C), r is
in meters (m) and Fe is in Newtons (N).

8. Quantum of Electric Charge
• Electric charge is quantized. The
smallest possible unit is the charge
on one electron or one proton:
ee = 1.602 x 10-19 Coulombs
• No smaller charge has ever been
detected in an experiment.

9. Electric Force Vector
• The force on a point charge q1 exerted
by another point charge q2 separated
by a distance r21 is:
 kq1q2  
F12 = 2 r21 ˆ F21 = − F12
r21
ˆ
where r21 is a unit vector along the axis
joining q2 and q1.

10. Principle of Superposition
• For a system of N charges q1, q2, q3, …, qN,
the resultant force F1 on q1 exerted by
charges q2, q3, …, qN is:
   
F1 = F12 + F13 +  + F1N
• Each charge may be considered to exert a
force on q1 that is independent of the other
charges present.

11. Field Forces and Electric Field
• Field forces act through space even if there is
no contact (e.g. gravitational force).
• The ELECTRIC FIELD E is defined in terms
of the electric force that would act on a
positive test charge q0 :

 Fe
E= in N/C
q0

12. Electric Field
• The electric force on a positive test charge q0
at a distance r from a single charge q:
 qq0
Fe = k 2 rˆ
r
• The electric field at a distance r from a single
charge q:
  
 Fe q
E= =k 2 r
ˆ Fe = q0 E
q0 r

13. Electric Field due to
a Group of Charges:
 qi
E = k ∑ 2 ri
ˆ
i ri
ˆ
ri is a unit vector from qi to q0

14. Example Problem
Four point charges are at 2q q
the corners of a square a
of side a as shown.
b) Determine the
magnitude and direction a a
of the electric field at
the location of q.
c) What is the resultant a
force on q? 3q 4q

15. Electric Field from Continuous Charge
Distributions
• If a total charge Q is distributed continuously,
it may be sub-divided into elemental charges
dQ, each producing an electric field dE:
dQ dQ
dE = k 2 E = ∫ dE = k ∫ 2
r r
 dQ 1 dQ 1
E = k∫ 2 r =
ˆ ∫ r 2 rˆ k=
r 4πε 0 4πε0
ε0 = permittivity of free space

16. Uniform Charge Distributions
• Volume Charge Density: ρ=Q/V
• Surface Charge Density: σ=Q/A
• Linear Charge Density: λ=Q/l
Example:
• A continuous line of charge lies along the x-
axis, extending from x=x0 to positive infinity.
The line carries a uniform linear charge
density λ0. What are the magnitude and
direction of the electric field at the origin?

17. Example Problem:
Electric Field due to a Power Line
• A power line is suspended a constant
distance yo above the ground, and carries a
uniform linear charge density λo. Assume that
the wire is infinitely long and that the ground
is a flat plane. What are the magnitude and
direction of the electric field on the ground
immediately below the power line?

18. Electric Field Lines
Electric Field Lines:
• describe the direction of the electric field at any point
• The density of field lines is proportional to the
magnitude of the electric field.
• The directions of arrows indicate the direction of the
force on a positive test charge.
• Rules:
– Lines begin on + charge and end on – charge
– Number of lines approaching or leaving a charge
is proportional to the magnitude of the charge.
– Electric field lines may never cross.

19. Electric Field Lines: Conventions
Positive Point Charge Negative Point Charge

20. Electric Field lines