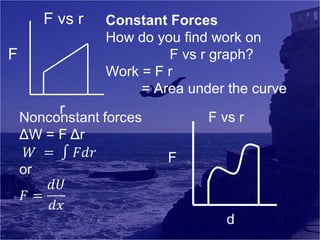
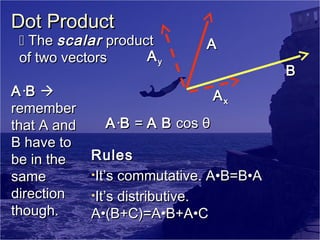
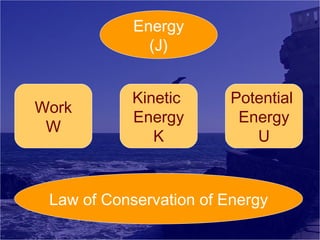
Work and energy can be summarized in 3 sentences: Energy is the ability to do work and exists in various forms. The work-energy theorem states that a change in kinetic energy is equal to the net work done on an object. The law of conservation of energy explains that energy cannot be created or destroyed, only transferred or changed from one form to another.

1. Work & Energy
In the past…
v, a, x, t  How things move, Kinematics
F, a, m  What makes them move, Dynamics
Now we will look at WHY they move!!! Energy!
Energy  The ability to do work.

2. Work =
Force x Displacement
1 Joule = 1 Newton x 1 Meter
1.
2.
3.
Object must move.
Force & Displacement must be on the
same plane
Don’t forget air friction is negligible.

3. Examples of work done on a box:
Work done by gravity? W = FG r = FG 0 = 0
Work done by the table? W = FTB r = FTB 0 = 0
Can the table ever do work on the box?
Work done by you?
W = F cosθ r
Work done by friction? W = FF r

4. How much work will the road do on an 1800 kg
car when its brakes are applied, if the
coefficient of friction between the road and the
wheels is 0.5 and the car skids 6 m?
W = F r = F f r = µ Fg r = µ m g r
= (0.5) (1800) (9.8) (6)
W = 52, 920 J

5. F vs r
F
Constant Forces
How do you find work on
F vs r graph?
Work = F r
= Area under the curve
r
F vs r
F
d

6. Dot Product
 The scalar product
Ay
of two vectors
A B 
remember
that A and
B have to
be in the
same
direction
though.
A
B
Ax
A B = A B cos θ
Rules
•It’s commutative. A•B=B•A
•It’s distributive.
A•(B+C)=A•B+A•C

7. Power = Work/Time
Power = (Force times distance) / time
Power = Force (distance/time)
Power = Force (velocity)
P = W/t or P = F v
Tells you how much energy you use in a
certain amount of time.
Metric Unit: Watts
English Unit: Horsepower.
746 Watts = 1 HP

8. Energy
(J)
Work
W
Kinetic
Energy
K
Potential
Energy
U
Law of Conservation of Energy

9. Energy
ability to do work

10. Kinetic Energy
 energy due to motion
K = ½ mv 2
How much KE does a 1800 kg car going 25
mph (11.2 m/s) have?
K = ½ (1800)(11.2)2 = 113 000 J
How much work would friction need to do to
stop it?
W = K = 113 000 J

11. Gravitational Potential Energy
 energy due to position
U G = mgh
Ex. You lift a 1.2 kg book from the first floor
to your social studies class on the 2nd floor
5 m up. How much potential energy does
the book have?
UG = m g h = (1.2) (9.8) (5) = 58.8 J
How much work did you do?
Conservation!!! W = UG = 58.8 J

12. Law of Conservation of Energy
 Energy cannot be created or destroyed
All the energy in = All the energy out
W + UG + KE = UG + KE (+ W)
(Work out is done by friction. If no
friction, then no work out.)

13. A 600 kg roller coaster car is lifted to the top of the first
hill, 55 m above the ground.
a. How much potential energy does it have?
UG = m g h
b. How much work was done to get the cart to the top
of the first hill?
W = UG
c. How fast is it going at the bottom of the first hill?
UG = K = ½ mv2
d. If the second hill is 40 m high, then how fast will the
cart be going when it crests the hill?
UG = UG + K

14. In the first car example, was there any
potential energy?
No W + 0 + K1 = 0 + K2 (+0)
W = K 2 – K1
W = ΔK
In the second example, was there any
kinetic energy at the beginning or the
end?
No W + UG1 + 0 = UG2 + 0 (+0)
W = UG2 – UG1
W = ΔUG

15. Work Energy Theorem
W = ΔK
W = Δ UG
In order to change any type of energy,
work must be done.

16. Sample Problem
A disgruntled physics student drops
her book off a 4 story building (12 m),
how fast is the book going before it
hits the ground?
h = 12 m
m = 1.7 kg
h = 12 m
Energy in = Energy out
UG + K = UG + K
Double check with kinematics!

18. A school bus pulls into an intersection. A car
traveling 35 km/h approaches and hits a patch
of ice. The driver locks the brakes causing the
car to slide toward the intersection. If the car
is originally 26 m away and the coefficient of
friction between the car’s tires and the icy road
is 0.25, does the car hit the bus and poor
innocent school children lose their lives … or
does the car stop just in the nick of time letting
the little children grow up to do physics
problems involving school buses and icy
roads?

19. Which of the following is an expression
for mechanical power?
a. Ft/m
b. F2m/a
c. Fm2/t
d. Fm/t
e. F2t/m

20. A pendulum consisting of a mass m attached to a
light string of length l is displaced from its rest
position, making an angle θ with the vertical. It is
then released and allowed to swing freely. Which
of the following expressions represents the
velocity of the mass when it reaches its lowest
position?
a. √(2gl(1-cos θ))
d. √(2gl (1-sin θ))
b. √(2gl tan θ)
e. √(2gl(cos θ-1))
c. √(2gl cos θ)

21. A mass m is moving horizontally along a nearly
frictionless floor with velocity v. the mass now
encounters a part of the floor that has a
coefficient of friction given by µ. The total
distance traveled by the mass before it is slowed
by friction to a stop is given by
a. 2v2/µg
b. v2/2µg
c. 2µgv2
d. µv2/2g
e. µvg

22. A 0.75 kg sphere is dropped through a tall
column of liquid. When the sphere has fallen
a distance of 2.0 m, it is observed to have a
velocity of 2.5 m/s.
a. How much work was done by the frictional
“viscosity” of the liquid?
b. What is the average force of friction during
the placement of 2.0 m?

23. *A rock of mass m is thrown
horizontally off a building from a m
height h, as shown. The speed
of the rock as it leaves the
thrower’s hand at the edge of
the building is vo. How much
h
time does it take the rock to
travel from the edge of the
building to the ground?
a. √(hvo)
b. h/vo
c. hvo/g
d. 2h/g
e. √(2h/g)
vo

24. *What is the kinetic energy of the rock
just before it hits the ground?
a. mgh
b. ½ mvo2
c. ½ mvo2 – mgh
d. ½ mvo2 + mgh
e. mgh – ½ mvo2

25. A 1.5 kg block is placed on an incline.
The mass is connected to a massless
spring by means of a light string passed
over a frictionless pulley, as shown. The
spring has a force constant k equal to 100
N/m. The block moves down a distance of
16 cm before coming to rest. What is the
coefficient of kinetic friction between the
block and the surface of the incline?
k = 100 n/m
1.5
kg
35°