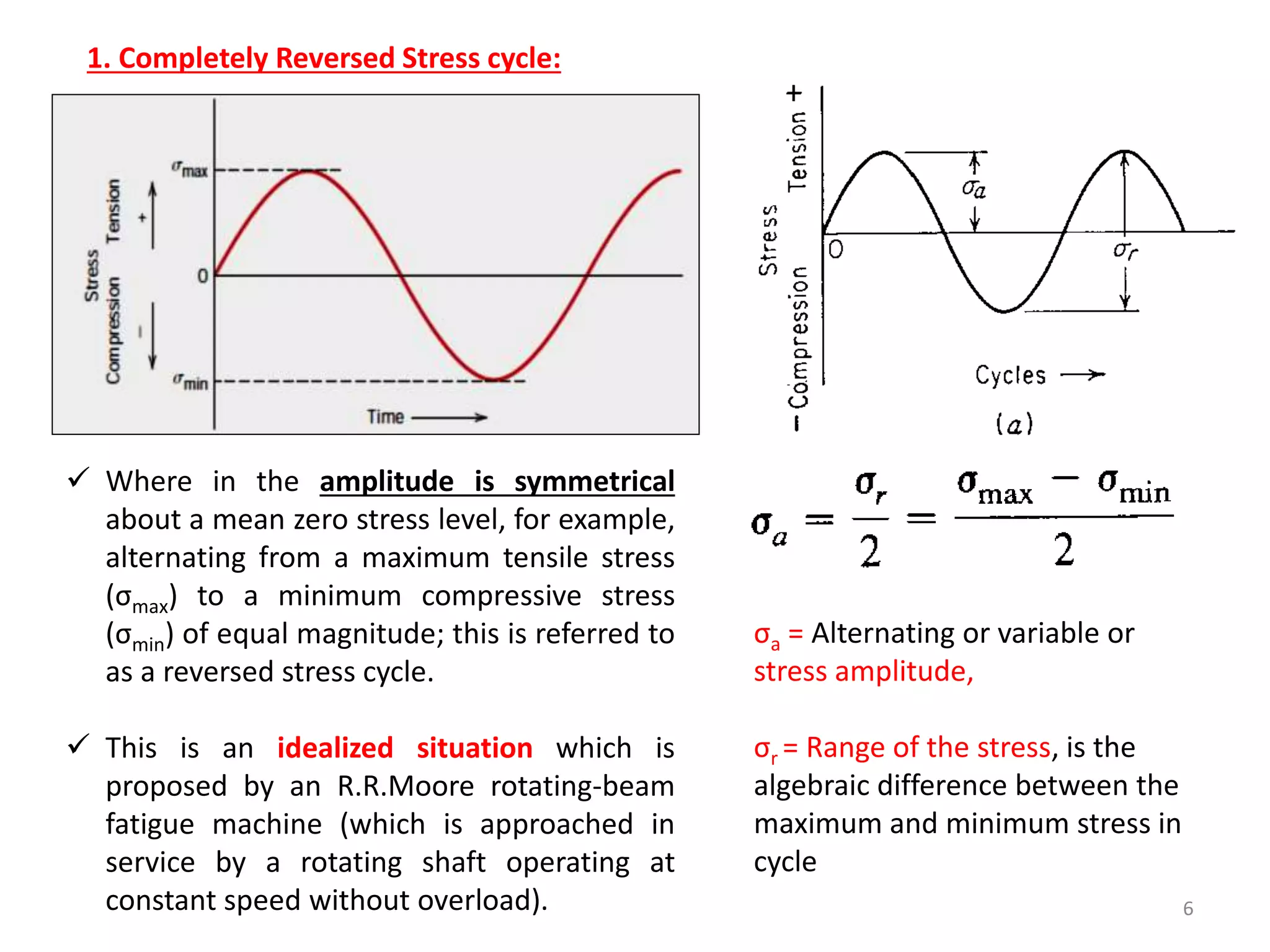
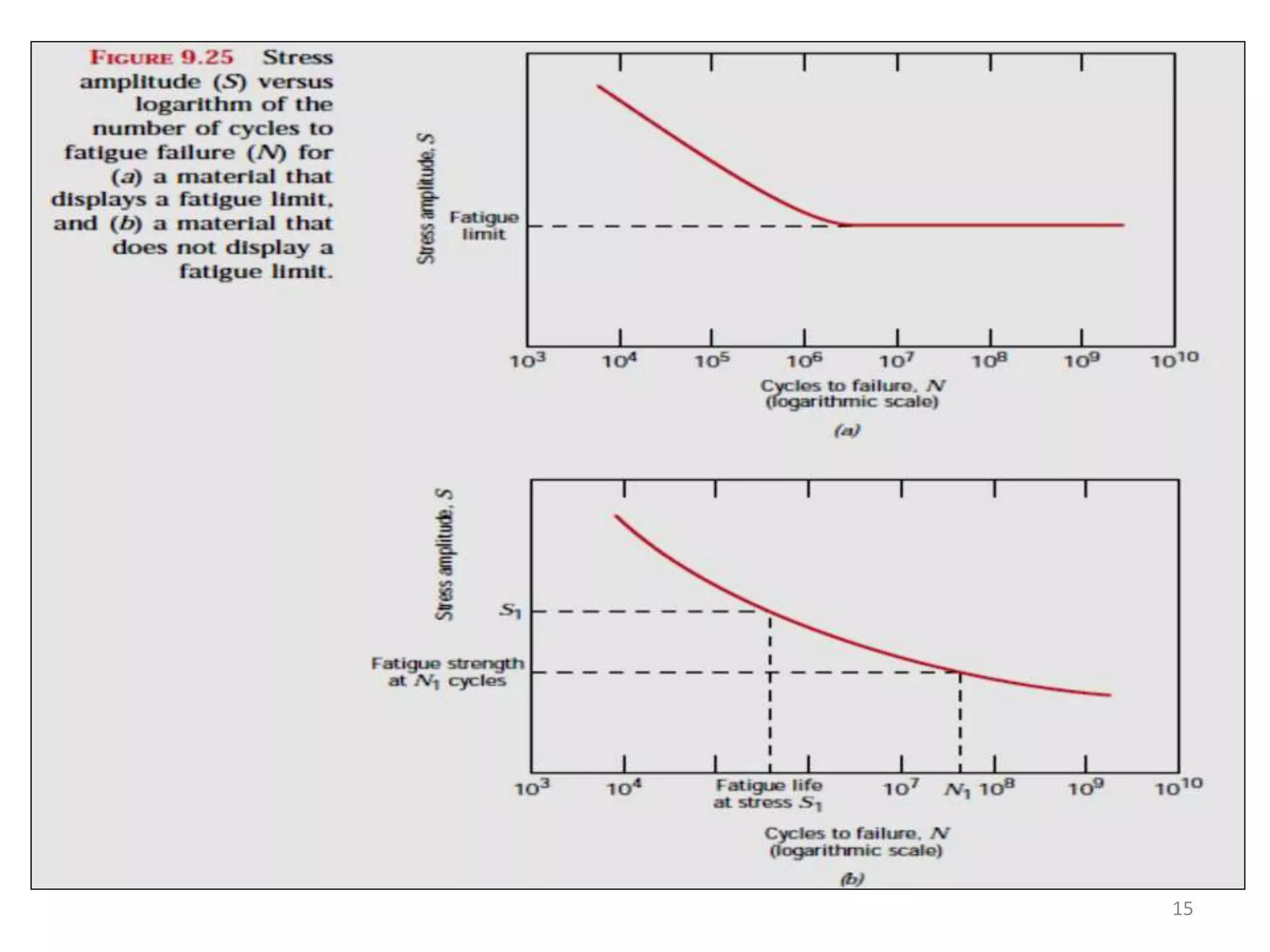
This document provides an introduction to fatigue, including: - Fatigue occurs when a component is subjected to fluctuating stresses and fails at a stress lower than its static strength. - It accounts for 90% of mechanical failures and occurs suddenly without warning. - Three factors are needed for fatigue failure: a maximum stress, stress variation, and sufficient number of cycles. - Fatigue testing involves subjecting specimens to cyclic stresses and recording the number of cycles until failure to generate an S-N curve.

1. Fatigue
B.E MYD
Muhammad Ali Siddiqui
1

2. Introduction to Fatigue
 It has been known since
1830 metal or a
component is subjected
to a repetitive or
fluctuation stresses it fails
at a stress much lower
than tensile or yield
strength for a static load.
 Failure occurs under
condition of dynamic and
fluctuation loading are
called Fatigue.
 Fatigue has become
progressively more
prevalent (common) as
technology has developed
a greater amount of
equipment's and
structure, such as
automobiles, aircraft,
compressor, pumps,
turbines, bridges etc.
2

3.  It is often stated that
fatigue accounts 90% of
all service failure due to
mechanical causes and it
will occur after lengthy
period of repeated stress
or strain cycle.
 Furthermore it is
catastrophic and
insidious (dangerous),
occurring very suddenly
and without warning.
 Fatigue failure is brittle-
appearing in nature, with
no dross plastic
deformation associated
with failure.
 Fatigue usually occurs at
a point of stress
concentration such as
sharp corner or notch or
at a metallurgical stress
concentration like an
inclusion.
3

4. Factors causes fatigue failure
 Three factors are necessary to
cause fatigue failure.
1. A maximum tensile stress of
sufficient high value.
2. A large enough variation or
fluctuation in the applied
stress.
3. A sufficient large number of
cycles of the applied stress.
 Other host Variables/Factors
are:
• stress concentration, corrosion,
temperature, overload,
metallurgical structure, residual
stresses and combined stresses
which tend to alter the
conditions of fatigue.
• Since we have not yet gained a
complete understanding of
what causes fatigue in metal.
4

5. Stress Cycle (Cyclic stresses)
• The applied stress may axial (tension,
compression), flexure (bending) or torsion
(twisting) in nature.
• In general three different fluctuation stress-
time modes are possible.
1. Completely Reversed Stress cycle:
2. Repeated Stress Cycle:
3. Irregular or random stress cycle
5

6. 6
1. Completely Reversed Stress cycle:
 Where in the amplitude is symmetrical
about a mean zero stress level, for example,
alternating from a maximum tensile stress
(σmax) to a minimum compressive stress
(σmin) of equal magnitude; this is referred to
as a reversed stress cycle.
 This is an idealized situation which is
proposed by an R.R.Moore rotating-beam
fatigue machine (which is approached in
service by a rotating shaft operating at
constant speed without overload).
σa = Alternating or variable or
stress amplitude,
σr = Range of the stress, is the
algebraic difference between the
maximum and minimum stress in
cycle

7. 7
2. Repeated Stress Cycle
The maxima and minima are asymmetrical
relative to the zero stress level. (σmax and σmin
stress are not equal)

8. 8
3. Irregular or random stress cycle
Finally, the stress level may vary randomly in amplitude and frequency. (complicated
stress cycle such as in aircraft wings etc)

9. The Fatigue Testing and S-N Curve
• *ASTM Standard
E 466, ‘‘Standard Practice for Conducting
Constant Amplitude Axial Fatigue Tests of
Metallic Materials,’’
E 468, ‘‘Standard Practice for Presentation of
Constant Amplitude Fatigue Test Results for
Metallic Materials.’’
9

10.  As with other mechanical
characteristics, the fatigue properties
of materials can be determined from
laboratory simulation tests.
 A test apparatus should be designed to
duplicate as nearly as possible the
service stress conditions (stress level,
time frequency, stress pattern, etc.).
 A schematic diagram of a rotating-
bending test apparatus, commonly
used for fatigue testing, is shown in
Figure;
 The compression and tensile stresses
are imposed on the specimen as it is
simultaneously bent and rotated.
 The basic method of presenting
engineering fatigue data is by means
of the S – N curve (a plot of stress
amplitude σa, S versus the logarithm of
the number of cycles to failure)
 The value of stress may be σmax, σmin,
 Most determination of the fatigue
properties of material have been made
in complete reverse bending mode,
where the mean stress σm, is zero
 σm = (σmax + σmin ) / 2 = 0
10

11. Different Fatigue Machines

12. Procedure
 A series of tests are commenced by subjecting a specimen
to the stress cycling at relatively large maximum stress
amplitude, usually on the order of two thirds of the static
tensile strength; the number of cycles to failure is counted.
 This procedure is repeated on other specimens at
progressively decreasing maximum stress amplitudes.
(Approx 8 to 12 specimen)
 This test stress is decreased for each succeeding specimen
until one or two specimens do not fail in the specified
number of cycles, which is usually at least 107 cycles. (as
shown in figure)
12

13. 13
Endurance limit or Fatigue limit, Fatigue strength and Fatigue life
 Two distinct types of S–N behavior are
observed, which are represented
schematically in Figure 9.25(ferrous
and non ferrous).
 As these plots indicate, the higher the
magnitude of the stress, the smaller
the number of cycles the material is
capable of sustaining before failure.
 For some ferrous (iron base) and
titanium alloys, the S–N curve (Figure
9.25a) becomes horizontal at higher N
values; or, there is a limiting stress
level, called the fatigue limit (also
sometimes the endurance limit),
below which fatigue failure will not
occur.
 This fatigue limit represents the
largest value of fluctuating stress that
will not cause failure for essentially an
infinite number of cycles.

14. 14
 For many steels, fatigue limits range
between 35 and 60% of the tensile
strength.
 Most nonferrous alloys (e.g., aluminum,
copper, magnesium) do not have a
fatigue limit, in that the S–N curve
continues its downward trend at
increasingly greater N values (Figure
9.25b).
 Thus, fatigue will ultimately occur
regardless of the magnitude of the
stress.
 For these materials, the fatigue response
is specified as fatigue strength, which is
defined as the stress level at which
failure will occur for some specified
number of cycles (e.g., 107 cycles).
 The determination of fatigue strength is
also demonstrated in Figure 9.25b.
 Another important parameter that
characterizes a material’s fatigue behavior is
fatigue life Nf. It is the number of cycles to
cause failure at a specified stress level, as
taken from the S–N plot (Figure 9.25b).

15. 15

16. Low - cycle and high-cycle fatigue
16
The fatigue behaviors represented in Figures
9.25a and 9.25b may be classified into two
domains.
1) Low-cycle fatigue:
 One is associated with relatively high loads
that produce not only elastic strain but also
some plastic strain during each cycle.
 Consequently, fatigue lives are relatively
short; this domain is termed low-cycle
fatigue and occurs at less than about 104
to 105 cycles. (N < 104 to 105 cycles)
2) High-cycle fatigue:
 For lower stress levels wherein
deformations are totally elastic, longer lives
result.
 This is called high-cycle fatigue in as much
as relatively large numbers of cycles are
required to produce fatigue failure.
 High-cycle fatigue is associated with fatigue
lives greater than about 104 to 105 cycles.
(N > 104 to 105 cycles)

17. Statistical Nature of Fatigue
• In determining the “fatigue limit” it should be recognized that
the specimen has its own fatigue limit of a material.
17

18. • The figure blow shows Summary of S-N curves, each based on
10 specimens, drawn from the same bar of steel
18

19. • Unfortunately, there always exists considerable scatter in
fatigue data as shown in figure above, that is, a variation in the
measured N value for a number of specimens tested at the
same stress level.
• This may lead to significant design uncertainties when fatigue
life and/or fatigue limit (or strength) are being considered.
• The scatter in results is a consequence of the fatigue sensitivity
to a number of test and material parameters that are
impossible to control precisely.
• These parameters include specimen fabrication and surface
preparation, metallurgical variables, specimen alignment in the
apparatus, mean stress, and test frequency.
19

20. • Several statistical techniques have been developed to specify
fatigue life and fatigue limit in terms of probabilities.
Example1:
20
• A distribution
of fatigue life at
constant stress
is illustrated
schematically in
the figure 12-4.
• Curves of
constant
probability (P)
of failure are
drawn

21. • Thus at stress σ1, 1 percent (P = 0.01) of the specimens
would be expected to fail at N1 …50 percent (P= 0.50) at
N2 and so on.
• The figure indicates a decreasing scatter in fatigue life
with increasing stress level.
• The statistical distribution function which describes the
distribution of fatigue life at constant stress is not
accurately known, for this would require the testing of
over 1,000 identical specimens under identical
condition at constant stress.
• It is now recognized that the “fatigue limit” is really a
“statistical quantity” which requires special techniques
for an accurate determination.
21

22. • Example 2: One convenient way of representing data treated in this
manner is with a series of constant probability curves, several of which are
plotted in Figure 9.26.
22
• The P value associated with each curve represents the probability of
failure. For example, at a stress of 200 MPa (30,000 psi),
• We would expect 1% of the specimens to fail at about 106 cycles and
50% to fail at about 2x107 cycles, and so on.

23. • It should be remembered that S–N curves
represented in the literature are normally
average values, unless noted otherwise.
• Fatigue S–N curves similar to those shown in
Figure 9.25 represent ‘‘best fit’’ curves which
have been drawn through average-value data
points.
• It is a little unsettling to realize that
approximately one half of the specimens tested
actually failed at stress levels lying nearly 25%
below the curve (as determined on the basis of
statistical treatments).
23

24. 24

25. Effect of Mean Stress on Fatigue
• Much of the fatigue data in the literature have
been determined for conditions of completely
reserved cycles of stress, σm = 0.
• However there are several possible methods
of determining an S-N diagram for a situation
where the mean stress is not equal to zero,
σm ≠ 0
25

26. 26
• The following figure shows the most common method of presenting
the data.
• In figure (a): the maximum stress is
plotted against log N for constant
values of the stress ratio R = σmin/ σmax.
• The is achieved by applying a series of
stress cycle with decreasing maximum
stress and adjusting the minimum
stress in each case so that it is a
constant fraction of the maximum
stress.
• The case of completely reversed stress
is given at R = -1.0.
• Note that as R becomes more positive,
which is equivalent to increasing the
mean stress; the measured fatigue limit
becomes grater.

27. Mechanism of Fatigue Failure
• The process of fatigue failure is characterized by three distinct
steps:
(1)Crack initiation, wherein a small crack forms at some point of high
stress concentration;
(2)Crack propagation, during which this crack advances
incrementally with each stress cycle; and
(3)Final failure, which occurs very rapidly once the advancing crack
has reached a critical size.
• The fatigue life Nf , the total number of cycles to failure, therefore
can be taken as the sum of the number of cycles for crack initiation
Ni and crack propagation Np
Nf = Ni + Np
• The contribution of the final failure step to the total fatigue life is
insignificant since it occurs so rapidly.
27

28. • Relative proportions to the total life of Ni and Np depend on the particular
material and test conditions.
• At low stress levels (i.e., for high-cycle fatigue), a large fraction of the
fatigue life is utilized in crack initiation. With increasing stress level, Ni
decreases and the cracks form more rapidly.
• Thus, for high stress levels (i.e, for low-cycle fatigue ), the propagation
step predominates (i.e., Np > Ni).
• Cracks associated with fatigue failure almost always initiate (or nucleate)
on the surface of a component at some point of stress concentration.
• Crack nucleation sites include surface scratches, sharp fillets, keyways,
threads, dents, and the like.
• In addition, cyclic loading can produce microscopic surface discontinuities
resulting from dislocation slip steps which may also act as stress raisers,
and therefore as crack initiation sites.
28

29. 29
• Once a stable crack has nucleated, it then initially propagates very slowly
and, in polycrystalline metals, along crystallographic planes of high shear
stress; this is sometimes termed stage I propagation (Figure 9.28).
• This stage may constitute (make) a
large or small fraction of the total
fatigue life depending on stress level
and the nature of the test specimen;
high stresses and the presence of
notches favor a short lived stage I.
• In polycrystalline metals, cracks
normally extend through several grains
during this propagation stage. The
fatigue surface that is formed during
stage I propagation has a flat and
featureless appearance.

30. • Eventually (finally), a second propagation stage (stage II)
takes over, wherein the crack extension rate increases
dramatically.
• Furthermore, at this point there is also change in
propagation direction to one that is roughly perpendicular
to the applied tensile stress (see Figure 9.28).
• During this stage of propagation, crack growth proceeds by
a repetitive plastic blunting and sharpening process at the
crack tip, a mechanism illustrated in Figure 9.29.
30

31. 31

32. • At the beginning of the stress cycle (zero or maximum
compressive load), the crack tip has the shape of a
sharp double-notch (Figure 9.29a).
• As the tensile stress is applied (Figure 9.29b), localized
deformation occurs at each of these tip notches along
slip planes that are oriented at 45o angles relative to
the plane of the crack.
• With increased crack widening, the tip advances by
continued shear deformation and the assumption of a
blunted (dull rounded) configuration (Figure 9.29c).
• During compression, the directions of shear
deformation at the crack tip are reversed (Figure 9.29d)
until, at the culmination (peak) of the cycle, a new
sharp double-notch tip has formed (Figure 9.29e).
32

33. • Thus, the crack tip has advanced a one-notch distance
during the course of a complete cycle.
• This process is repeated with each subsequent cycle
until eventually some critical crack dimension is
achieved that precipitates the final failure step and
catastrophic failure results.
• The region of a fracture surface that formed during
stage II propagation may be characterized by two types
of markings termed beachmarks and striations.
33

34. 34
Figure: Fatigue fracture surface. (a) At low magnifications, the beach
mark pattern indicates fatigue as the fracture mechanism. The arrows
show the direction of growth of the crack front, whose origin is at the
bottom of the photograph. (Image (a) is from C.C. Cottell, ‘‘Fatigue
Failures with Special Reference to Fracture Characteristics,’’ Failure
Analysis: The British Engine Technical Reports, American Society for
Metals, 1981, p. 318.) (b) At very high magnifications, closely spaced
striations formed during fatigue are observed (x 1000)

35. 35
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
Figure :
Schematic
representation of a
fatigue fracture surface
in a steel shaft,
showing the initiation
region, the propagation
of fatigue crack (with
beam markings), and
catastrophic rupture
when the crack length
exceeds a critical value
at the applied stress

36. 36
Fatigue Failure Analysis of a Crankshaft
Example
A crankshaft in a diesel engine fails. Examination of the crankshaft
reveals no plastic deformation. The fracture surface is smooth. In
addition, several other cracks appear at other locations in the crankshaft.
What type of failure mechanism would you expect?
Solution
Since the crankshaft is a rotating part, the surface experiences cyclical
loading. We should immediately suspect fatigue. The absence of plastic
deformation supports our suspicion. Furthermore, the presence of other
cracks is consistent with fatigue; the other cracks didn’t have time to
grow to the size that produced catastrophic failure. Examination of the
fracture surface will probably reveal beach marks or fatigue striations.

37. 37
Example
Automobile Axle Failure Analysis. An engineer investigating the cause of an
automobile accident finds that the right rear wheel has broken of at the axle.
The axle is bent. The fracture surface reveals a Chevron pattern pointing
toward the surface of the axle. Suggest a possible cause for the fracture.
Solution
• The Chevron pattern indicates that the wheel was subjected to an
intense impact blow, which was transmitted to the axle, causing failure.
• Further examination of the fracture surface, microstructure, composition,
and properties may verify that the axle was manufactured properly.
Automobile Axle Failure Analysis

38. Factors that affect fatigue-life
1. Cyclic stress state: Depending on the
complexity of the geometry and the loading,
one or more properties of the stress state
need to be considered, such as stress
amplitude, mean stress, biaxiality, in-phase
or out-of-phase shear stress, and load
sequence,
2. Geometry: Notches and variation in cross
section throughout a part lead to stress
concentrations where fatigue cracks initiate.
38

39. 3. Surface quality. Surface roughness cause microscopic
stress concentrations that lower the fatigue strength.
Compressive residual stresses can be introduced in the
surface by e.g. shot peening to increase fatigue life. Such
techniques for producing surface stress are often referred
to as peening, whatever the mechanism used to produce
the stress. Low plasticity burnishing, laser peening, and
ultrasonic impact treatment can also produce this surface
compressive stress and can increase the fatigue life of the
component. This improvement is normally observed only
for high-cycle fatigue.
4. Material Type: Fatigue life, as well as the behavior
during cyclic loading, varies widely for different materials,
e.g. composites and polymers differ markedly from
metals.
39

40. 5. Residual stresses: Welding, cutting, casting, and
other manufacturing processes involving heat or
deformation can produce high levels of tensile
residual stress, which decreases the fatigue
strength.
6. Size and distribution of internal defects: Casting
defects such as gas porosity, non-metallic inclusions
and shrinkage voids can significantly reduce fatigue
strength.
7. Direction of loading: For non-isotropic materials,
fatigue strength depends on the direction of the
principal stress.
40

41. 8. Grain size: For most metals, smaller grains yield
longer fatigue lives, however, the presence of
surface defects or scratches will have a greater
influence than in a coarse grained alloy.
9. Environment: Environmental conditions can
cause erosion, corrosion, or gas-phase
embrittlement, which all affect fatigue life.
Corrosion fatigue is a problem encountered in many
aggressive environments.
10. Temperature: Extreme high or low
temperatures can decrease fatigue strength.
41

42. Crack Growth Rate
• In many cases, a component may not be in
danger of failure even a crack is present.
• To estimate when failure occur; rate of crack
propagation become important.
• Following figure shows the crack growth rate v/s
range of the stress intensity factor ΔK, which
characterizes crack geometry and stress
amplitude.
42

43. 43
Figure : Crack growth rate
versus stress-intensity factor
range for a high-strength
steel.
For this steel, C = 1.62  1012
and n = 3.2 for the units
shown.
CrackGrowthrate(m/cycles) Crack Growth Rate
Crack growth rate given by:
𝒅𝒂
𝒅𝑵
= 𝑪 ∆𝑲 𝒏 Eq:01
∆𝐾 = 𝐾𝐼𝐶𝑚𝑎𝑥 −
𝐾𝐼𝐶𝑚𝑖𝑛
∆𝐾 = Y σ 𝑚𝑎𝑥 𝜋𝑎 − Y σ 𝑚𝑖𝑛 𝜋𝑎
∆𝐾 = Y∆σ2 𝜋𝑎

44. • Below Threshold ΔK= crack does not grow
• For some what higher stress-intensities, crack
grow slowly.
• And still higher intensities a crack grow at a rate
of given by
𝒅𝒂
𝒅𝑵
= 𝑪 ∆𝑲 𝒏 Eq:01
• When ΔK is still higher, crack grow in a rapid and
unstable manner until fracture occurs.
44
Crack Growth Rate

45. • Knowledge of crack growth rate is of assistance in designing
component and in nondestructive evaluation to determine if a crack
poses imminent danger to the structure.
• One approach to this problem is to estimate the number of cycle
required before failure occurs. By rearranging Equation 01 and
substituting for ∆𝐾: and integrate this b/w the initial size of the crack
and the crack size required for fracture to occur, we find that.
𝑁 =
2[(𝑎 𝑐)
2−𝑛
2 − 𝑎𝑖
2−𝑛
2 ]
2 − 𝑛 𝐶Y 𝑛∆σ 𝑛π 𝑛/2
• ai = initial Flaw size
• ac = flaw size required to fracture.
• C and n = are empirical constant depends upon the material.
45

46. 46
Design of a Fatigue-Resistant Plate
Example:
A high-strength steel plate (Figure 6.52), which has a
plane strain fracture toughness of 80 MPa , is
alternately loaded in tension to 500 MPa and in
compression to 60 MPa. The plate is to survive for
10 years, with the stress being applied at a
frequency of once every 5 minutes. Design a
manufacturing and testing procedure that assures
that the component will serve as intended.
m
For High strength steel, C = 1.62  1012 and n = 3.2 for the units shown.

47. 4747
SOLUTION

48. The End
48