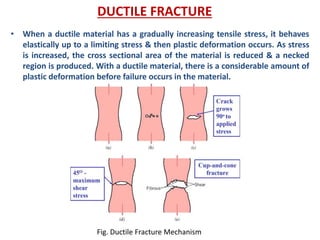
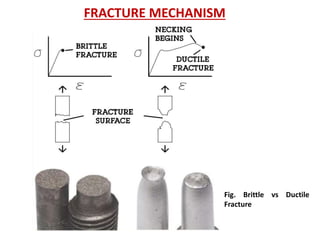
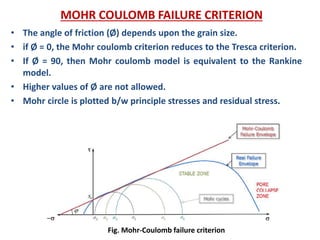
- Fracture is the separation of an object into pieces due to stress. There are two main types: ductile fracture and brittle fracture. - Ductile fracture involves plastic deformation and occurs through processes like necking and the formation and coalescence of microvoids. It results in a cup-and-cone pattern. Brittle fracture occurs suddenly without plastic deformation. - Fracture mechanics studies how cracks propagate in materials. The Griffith theory and models like the Mohr-Coulomb criterion describe how stresses lead to fracture based on factors like crack size and material properties.

1. FRACTURE
• Simple fracture is the separation of a body into two or more
pieces in response to an imposed stress that is static (i.e.,
constant or slowly changing with time)
A fracture is the separation of an object or material into two or
more pieces under the action of stress.
• The fracture of a solid usually occurs due to the development
of certain displacement discontinuity surfaces within the solid.
• If a displacement develops perpendicular to the surface of
displacement, it is called a normal tensile crack or simply a
crack; if a displacement develops tangentially to the surface of
displacement, it is called a shear crack, slip band, or
dislocation.
• Fracture strength or breaking strength is the stress when a
specimen fails or fractures.

2. FRACTURE MECHANISM
• Fracture mechanics is the field of mechanics concerned with the
study of the propagation of cracks in materials.
• In modern materials science, fracture mechanics is an important tool
in improving the mechanical performance of mechanical
components. It applies the physics of stress & strain, in particular
the theories of elasticity & plasticity, to the microscopic
crystallographic defects found in real materials in order to predict
the macroscopic mechanical failure of bodies.
Mode I:
Opening
Mode II:
In-plane shear
Mode III:
Out-of-plane shear

3. • When a ductile material has a gradually increasing tensile stress, it behaves
elastically up to a limiting stress & then plastic deformation occurs. As stress
is increased, the cross sectional area of the material is reduced & a necked
region is produced. With a ductile material, there is a considerable amount of
plastic deformation before failure occurs in the material.
DUCTILE FRACTURE
Fig. Ductile Fracture Mechanism

4. Necking:
Necking, in engineering or
materials science, is a mode of
tensile deformation where
relatively large amounts of strain
localize disproportionately in a
small region of the material. With
elastic strain the material
becomes plastically deformed &
neck formation process starts.
Deformation of material depends
upon material purity.
STEPS IN DUCTILE FRACTURE
Necking
Small cavities forming:
Within the neck, small cavities or voids
are formed. These develop as a result of
the stress causing small particles of
impurities or other discontinuities in the
material to either fracture or separate
from metal matrix. More such nuclei are
available to trigger the development of
these cavities, the less the material will
extend before fracture & less ductile the
material. As purity of material increases,
ductility of the material also increases.

5. Formation of Crack:
Small cavities, or micro voids,
form in the interior of the cross
section enlarge, come together, &
coalesce to form an elliptical
crack, which has its long axis
perpendicular to the stress
direction. The crack continues to
grow in a direction parallel to its
major axis by this micro void
coalescence process.
STEPS IN DUCTILE FRACTURE
Cup & Cone Fracture:
Finally, fracture ensues by the rapid
propagation of a crack around the outer
perimeter of the neck by shear deformation
at an angle of about 45 degree with the
tensile axis this is the angle at which the
shear stress is a maximum. Some times a
fracture having this characteristic surface
contour is termed a cup-and-cone fracture
because one of the mating surfaces is in the
form of a cup, the other like a cone.
Cup-and-cone fracture
in aluminum

6. BRITTLE FRACTURE
• Brittle fracture takes place without any appreciable deformation and
by rapid crack propagation. The direction of crack motion is very
nearly perpendicular to the direction of the applied tensile stress
and yields a relatively flat fracture surface.
• When gradual tensile load is applied on material on tensile test, at
the end of elastic limit, without any prior indication material breaks.
This type of fracture is called as Brittle Fracture.
Brittle fracture in a mild
steel

7. FRACTURE MECHANISM
Fig. Brittle vs Ductile
Fracture

8. • Fracture mechanics was developed during world war I by English aeronautical
engineer, A.A. Griffith, to explain the failure of brittle materials. According to
Griffith, there are micro cracks in the metal that causes local concentration of
stress to values high enough to propagate the crack & eventually to fracture
of metal.
• Consider a thin plate of length (l) having a thru-crack of length 2c, as shown in
Fig 3. The upper curve shows the force-deflection curve for a non-extending
crack of length 2c. For a non-extending crack of length 2(c + Δc), the curve will
be the lower curve. The area between these two curves represents the
energy released to extend the crack from 2c to 2(c + Δc).
GRIFFITH THEORY OF BRITTLE FRACTURE
Fig. Explanation of Griffith Theory of Brittle Fracture

9. Using elasticity theory Griffith showed that the energy released per unit
thickness during a crack growth of 2Δc is
The creation of additional crack surface requires surface energy per unit
thickness given by
GRIFFITH THEORY OF BRITTLE FRACTURE

10. Thus, the critical stress is inversely proportional to c½. Hence, the smaller the
flaw, the greater the value of σc. The Griffith theory is good for every brittle
material like glass, in which failure occurs without any plastic deformation.
When there is some plastic deformation associated with the crack extension, we
must add the plastic work γp expended in making the surface to the surface
energy term γs to obtain σc as shown below:
The above equation forms the starting point of the modern fracture mechanics.
GRIFFITH THEORY OF BRITTLE FRACTURE

11. Two widely used yield criterion:
1. Tresca criterion or maximum shear stress criterion.
2. Von Mises criterion or distortion energy criterion.
Tresca Criterion:
Tresca found that plastic flow in a metal begins when tangential stress attains
a value.
Assume that a body is subjected to triaxial stresses. σ1 σ2, σ3 are principal
stresses and σ1 > σ2 > σ3 (algebraically).
Then maximum shear stress
When T max exceeds a certain value “c”, specific to that material, yielding will
occur. To find the value of “c”, the material is subjected to uniaxial tensile test
and find out yield point strength (σ0).
YIELD CRITERION

12. i) For uniaxial tensile test, stress situation is
ii) Material is subjected to pure shear:
K =
σ0
𝟐
= 0.5 σ0
TRESCA CRITERION

13. Von Mises Criterion:
According to this criterion, yielding will occur when shear strain energy per
unit volume reaches a critical value. The shear strain energy per unit volume is
expected terms of three principal stresses:
G= modulus of shear which is a constant.
(i) For uniaxial tensile test, yielding will occur when σ1 = σ0; σ2 = σ3 = 0
Therefore Von Mises criterion can be stated as
• For Plane stress: σ2 = 0
• For plane strain: σ2 =
σ1+σ3
𝟐
VON MISES CRITERION

14. iii) For pure shear stress condition:
This is the relationship between yield strength and tensile strength of the
material as per Von Mises criterion.
Von Mises criterion satisfy the experimental data better than Tresca and
therefore K =
σy
𝟑
value is normally used.
VON MISES CRITERION

15. Advantages of Von Mises criterion:
• It overcomes major deficiency of Tresca criterion. Von Mises
criterion implies that yielding is not dependent on any particular
normal stress but instead, depends on all three principal shearing
stresses.
• Von Mises criterion conforms the experimental data better than
Tresca and therefore more realistic.
• Since it involves squared terms, the result is independent of sign of
individual stresses. This is an important since it is not necessary to
know which is the largest and the smallest principal stress in order
to use this criterion.
VON MISES CRITERION

16. TRESCA AND VON MISES CRITERION

17. VON MISES CRITERION

18. VON MISES CRITERION

19. MAXIMUM NORMAL STRESS THEORY
• This theory postulates, that failure will occur in the structural
component if the maximum normal stress in that component
reaches that ultimate strength, σu obtained from the tensile test
of a specimen of the same material.
• Thus, the structural component will be safe as long as the absolute
values of the principle stresses σ1 and σ2 are both less than σu:

20. MAXIMUM NORMAL STRESS THEORY
• This theory deals with brittle materials only.
• The maximum normal stress theory can be expresses graphically
as shown in the figure. If the point obtained by plotting the
values σ1 and σ2 of the principle stress fall within the square area
shown in the figure, the structural component is safe.
• If it falls outside that area, the component will fail.

21. MOHR COULOMB FAILURE CRITERION
• The variation of peak stress σ1 with confining pressure σ3 is
known as criterion of failure. The simplest and best known
criterion of failure is Mohr coulomb criterion.
• Many geotechnical analysis method require use of this strength
model.
• The Mohr coulomb criterion describe a linear relationship b/w
normal and shear stresses at failure.
• It represents the linear envelope that is obtained from a plot of the
shear strength of the material versus applied normal stress.
Tp = Si + σ tan Ø
Tp = Confinement
Si = Shear stress intercept
σ = Normal stress
Ø = Angle of internal friction

22. • The angle of friction (Ø) depends upon the grain size.
• if Ø = 0, the Mohr coulomb criterion reduces to the Tresca criterion.
• If Ø = 90, then Mohr coulomb model is equivalent to the Rankine
model.
• Higher values of Ø are not allowed.
• Mohr circle is plotted b/w principle stresses and residual stress.
Fig. Mohr-Coulomb failure criterion
MOHR COULOMB FAILURE CRITERION

23. • The value of σ1 and σ3 are obtained from the instrument.
• Shear intercept line indicates the peak shear strength.
• The radius of the circle describe the strength of rock/soil.
• Small radius of circle indicate the low strength of rock/soil. Large radius
indicate high strength of rock/soil.
• Each circle is the combination of maximum load and confined pressure.
• The point of tangency of circle with shear intercept line is the maximum
strength of that rock/soil.
• Ø is the angle of friction of the load on the plane of normal stresses.
• When the load increases to its maximum point the cracks are
produced and residual stresses released.
• Rocks having minimum cracks will have maximum residual stresses.
• Rock having fine grain particles will show greater strength.
• When there will be coarser grains then less stress will be apply to
create the failure as compare to fine grains.
MOHR COULOMB FAILURE CRITERION

24. Mohr coulomb criterion is not particularly satisfactory criterian for
rock/soil
It implies that a major shear fracture occurs at peak strength.
• The criterion is likely to give incorrect result if the failure mechanism
is not shear.
• It implies direction of shear failure which does not agree with
observation particularly in brittle rock/soil.
• It is linear and peak strength envelope determine experimentally are
usually no-linear.
• It will be noticed that only σ1 and σ3 are used and σ2 is ignore in case of
rock/soil sample.
LIMITATIONS

25. The Modified Mohr-Coulomb model is an advanced material model that can
simulate the behavior of different types of soil/rock. It is based on an elasto-
plastic formulation and can capture the basic properties of soil material, namely
a pressure dependent shear strength (with soil dilatancy), irrecoverable
compaction and nonlinear elastic unloading. This leads to a so-called double
hardening model:
• One yield-surface for shear failure and one yield-surface for compaction.
• The Modified Mohr-Coulomb model combines power-law nonlinear elastic
behavior, with exponential cap-hardening with Rowe's dilatancy rule.
• A parabolic hardening of the friction angle as function of the plastic shear-
strain.
MODIFIED MOHR COULOMB DIAGRAM