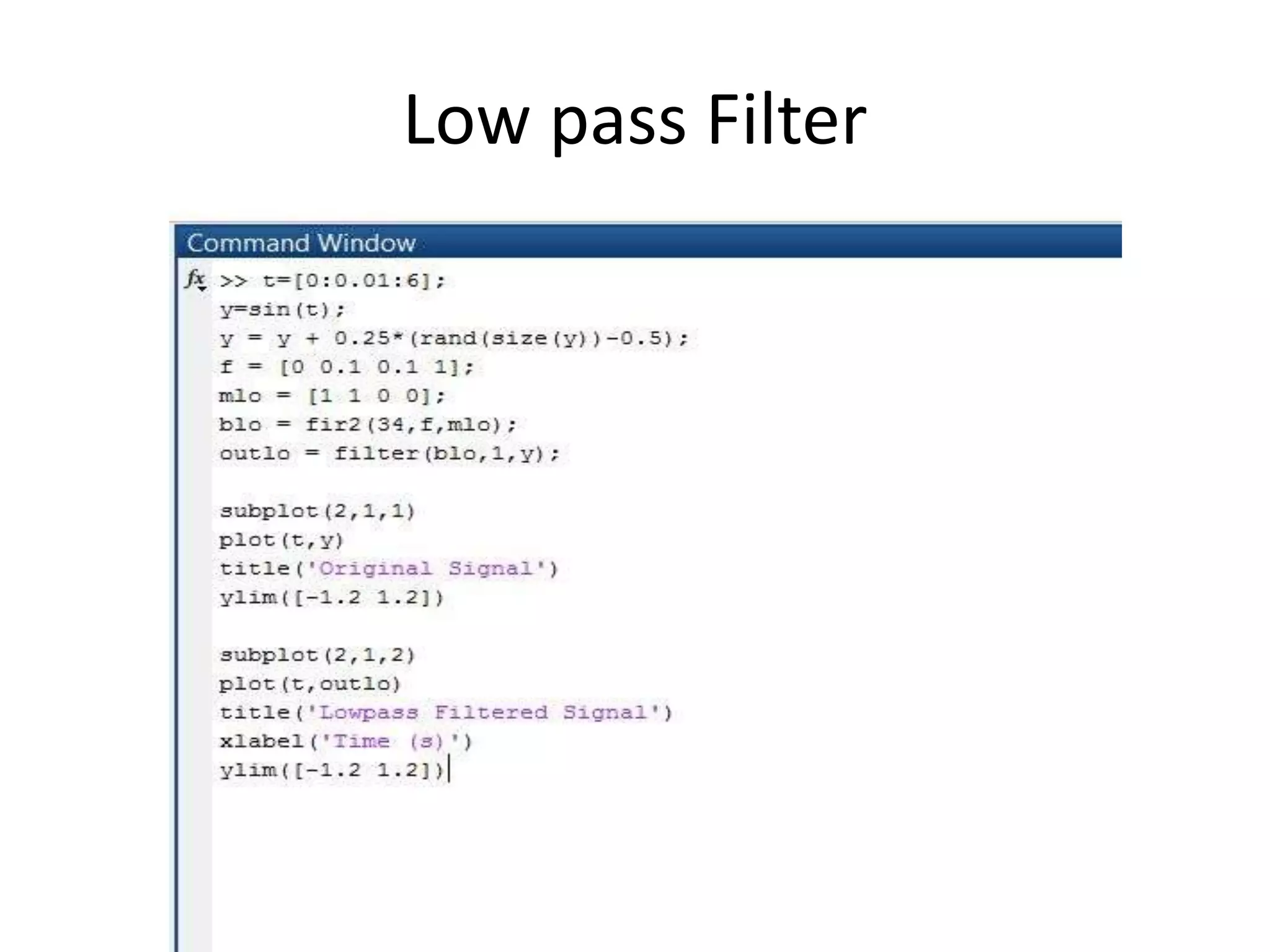
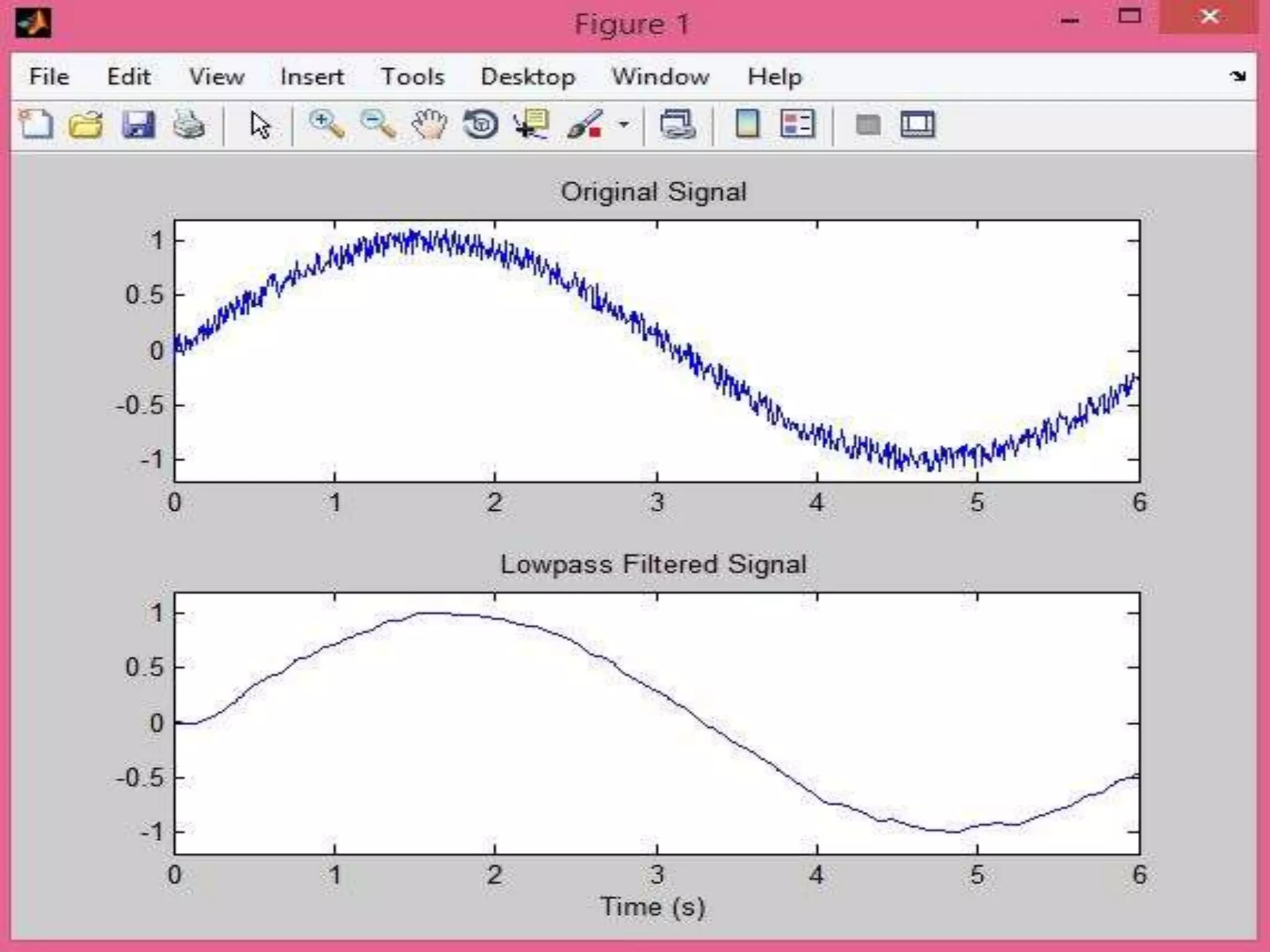
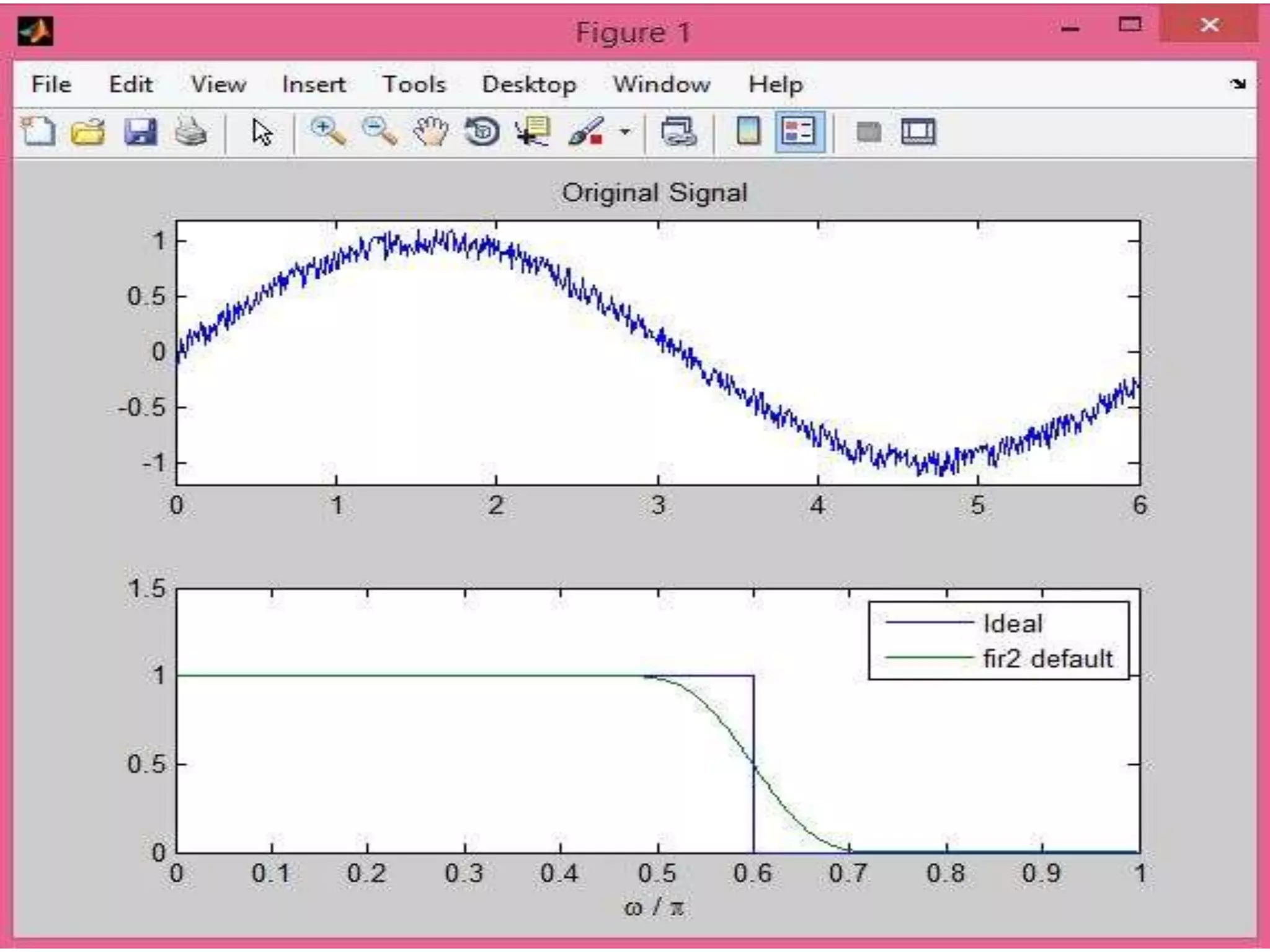
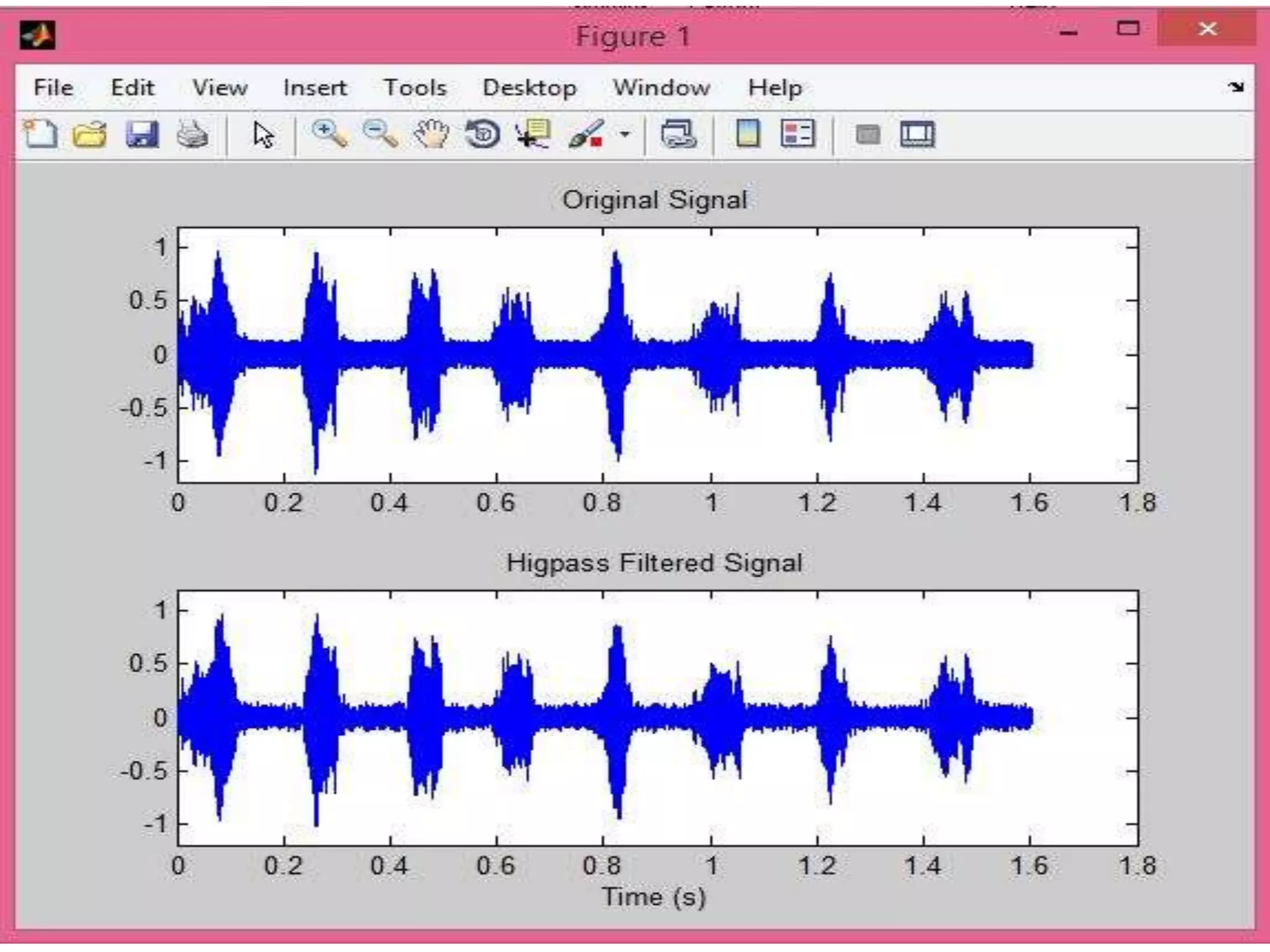
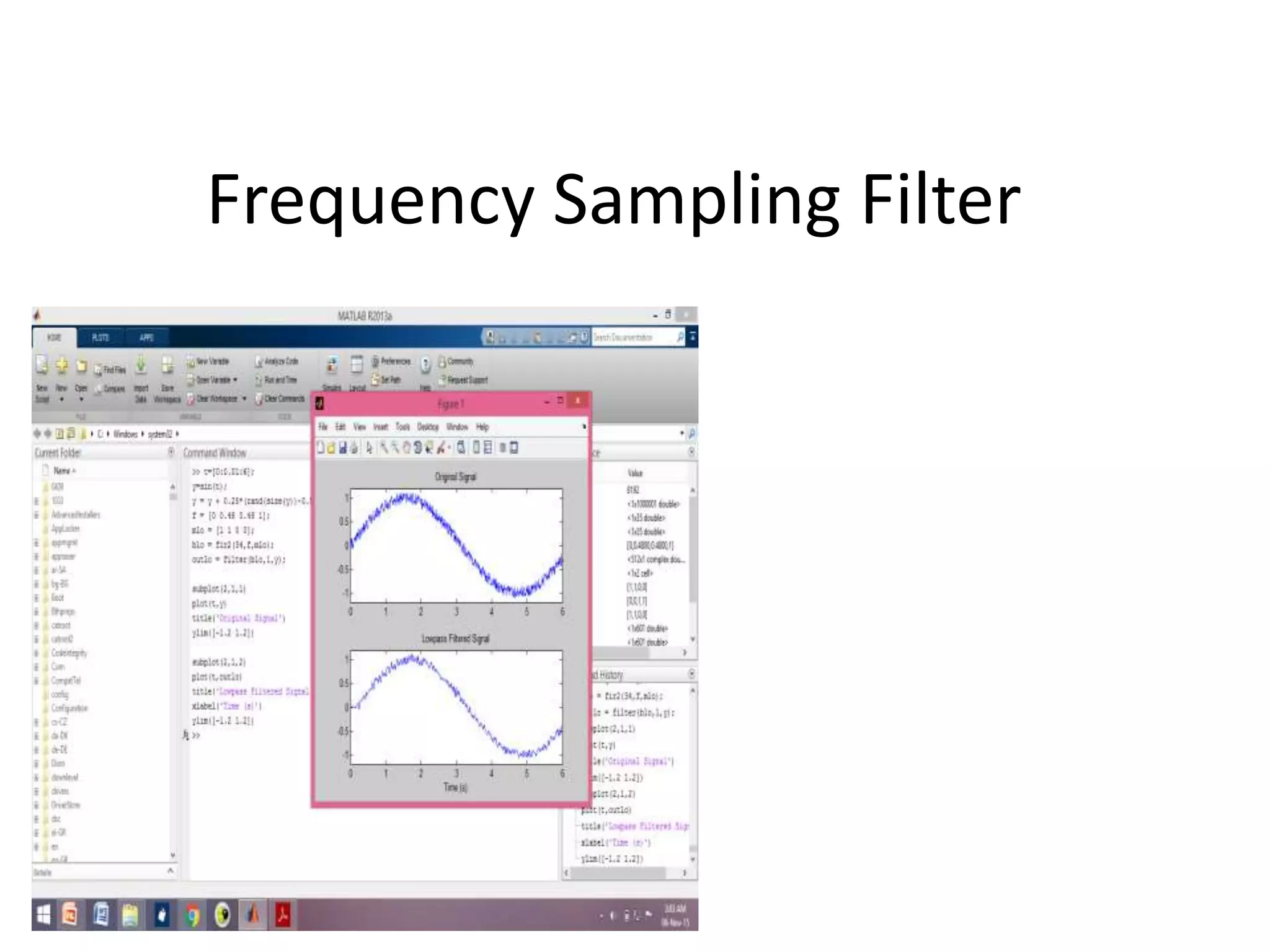
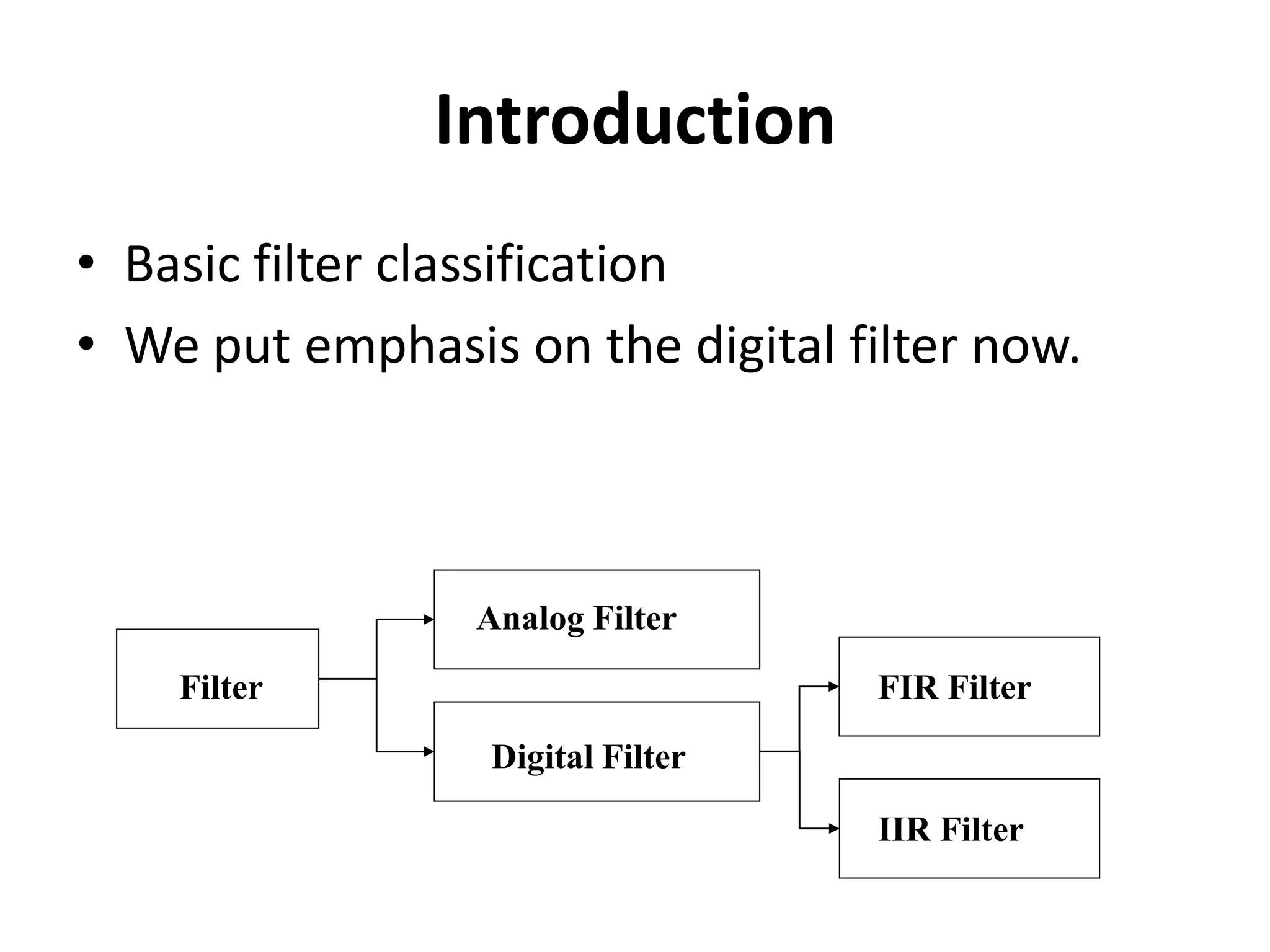
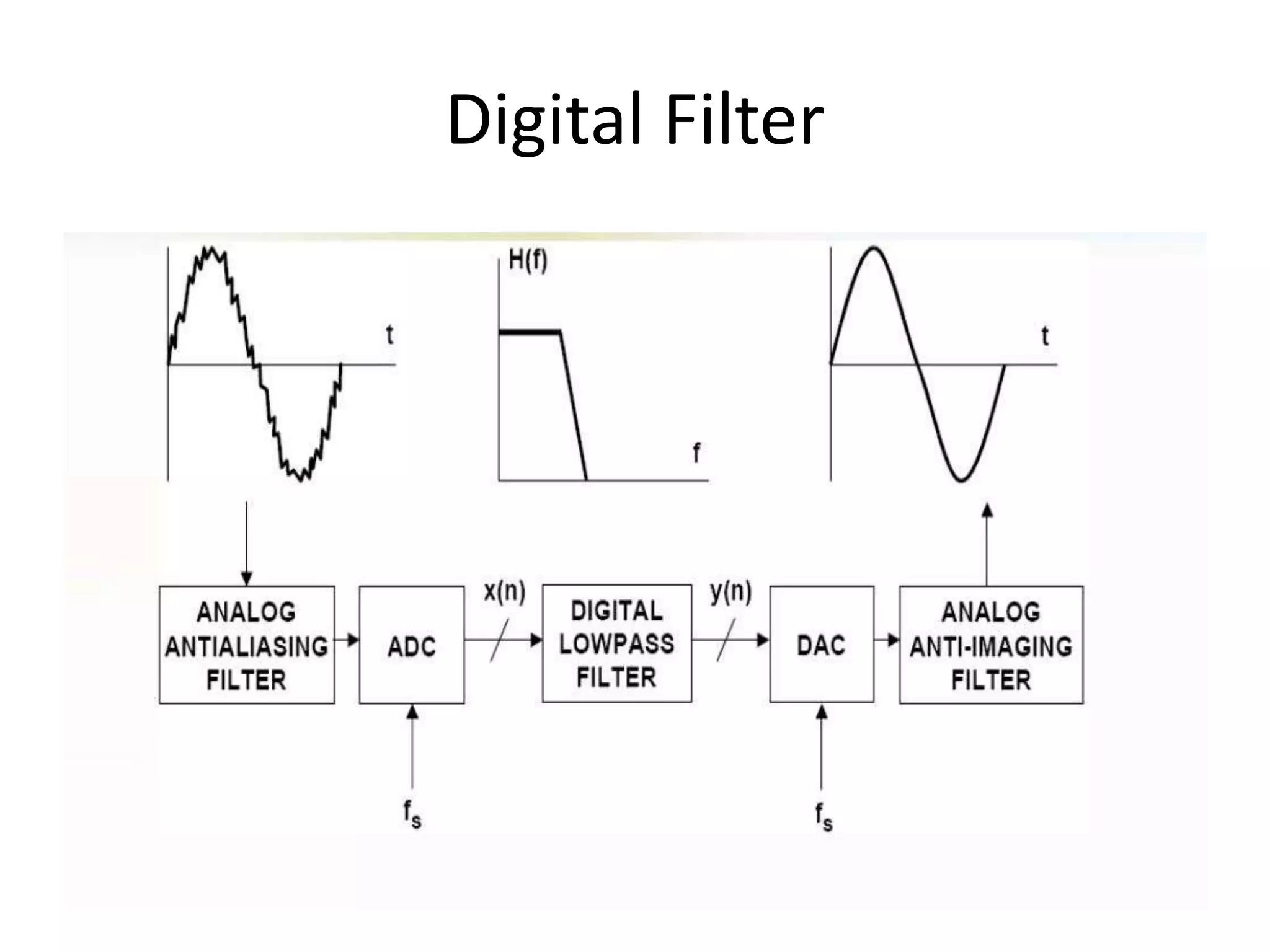
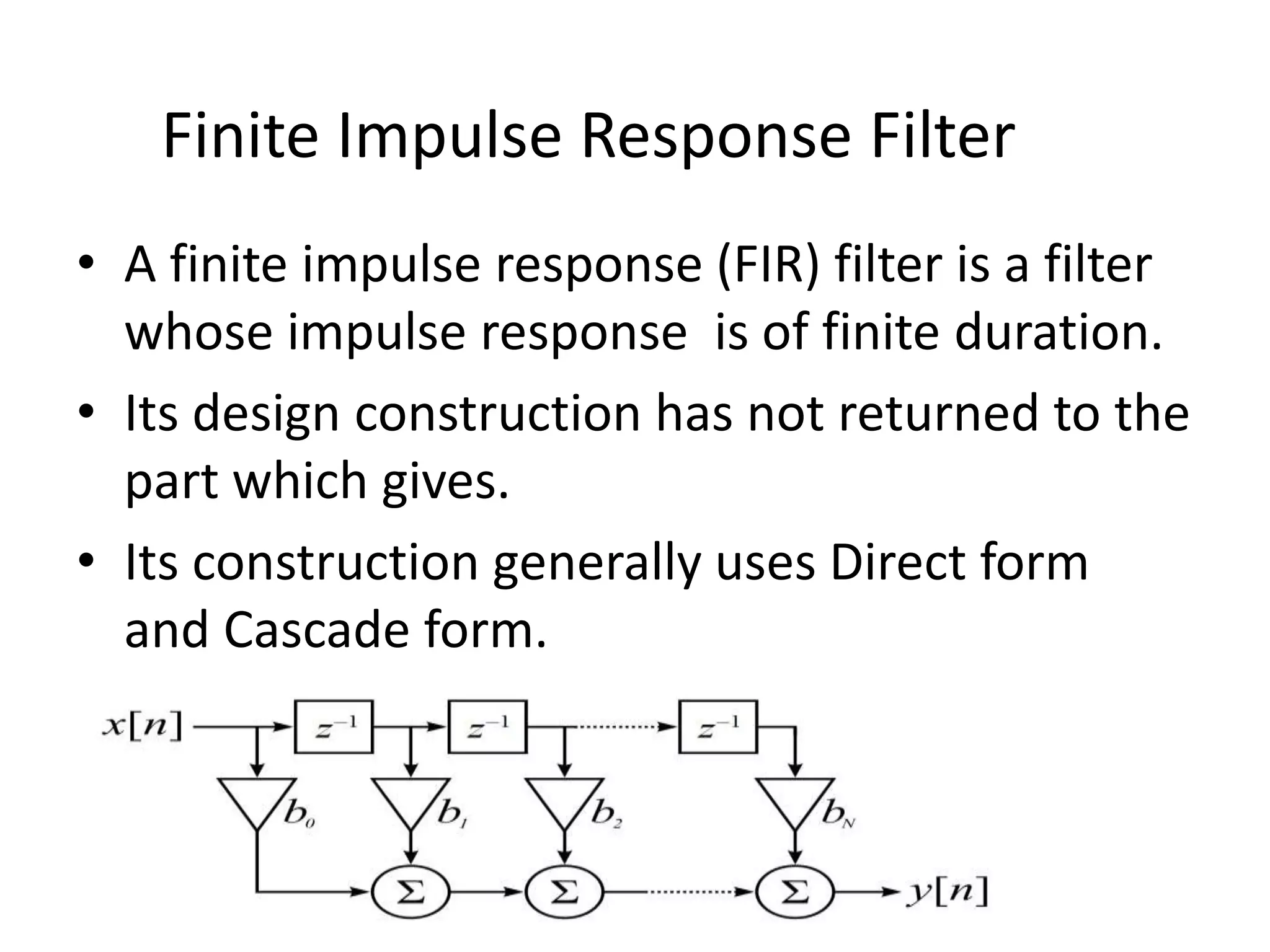
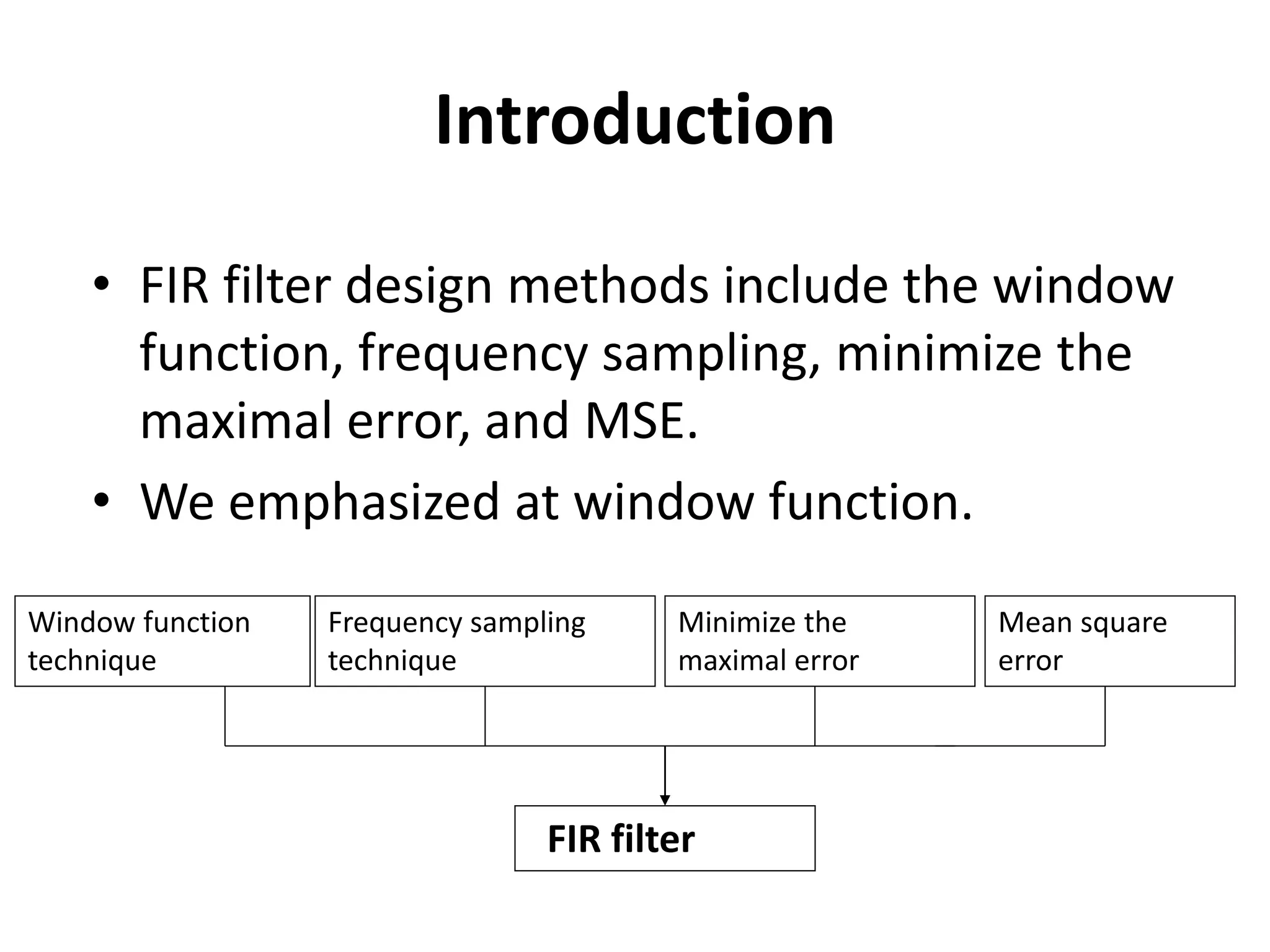
The document discusses electronic filters, emphasizing digital filters, particularly Finite Impulse Response (FIR) filters, which transform numerical sequences to enhance desired frequency components. It details FIR filter design methods, including the window function technique and frequency sampling, providing specific examples such as low and high pass filters designed using MATLAB. The implementation of these filters can be applied to DSP processors for noise reduction in electronic circuits.

1. Frequency Sampling Filter

2. Filter
• Electronic filters are circuits which perform
signal processing functions, specifically to
remove unwanted frequency components
from the signal, to enhance wanted ones, or
both.

3. Introduction
• Basic filter classification
• We put emphasis on the digital filter now.
Filter
Analog Filter
Digital Filter
IIR Filter
FIR Filter

4. Digital Filter

5. • Digital Filter: numerical procedure or
algorithm that transforms a given sequence of
numbers into a second sequence that has
some more desirable properties.
DIGITAL FILTER
Input sequence Output Sequence

6. • A finite impulse response (FIR) filter is a filter
whose impulse response is of finite duration.
• Its design construction has not returned to the
part which gives.
• Its construction generally uses Direct form
and Cascade form.
Finite Impulse Response Filter

7. Introduction
• FIR filter design methods include the window
function, frequency sampling, minimize the
maximal error, and MSE.
• We emphasized at window function.
Window function
technique
Frequency sampling
technique
Minimize the
maximal error
FIR filter
Mean square
error

8.  The basic idea behind the window design is to choose a
proper ideal frequency-selective filter (which always has a
noncausal, infinite-duration impulse response) and then to
truncate (or window) its impulse response to obtain a linear-
phase and causal FIR filter.
 Therefore the emphasis in this method is on selecting an
appropriate windowing function and an appropriate ideal
filter. We will denote an ideal frequency-selective filter by
,which has a unity magnitude gain and linear-phase
characteristics over its passband, and zero response over its
stopband.
FIR Filter Design by Window function
technique

9. FIR Filter Design by Window function
technique
• Simplest FIR the filter design is window
function technique
• A supposition ideal frequency response may
express
where
( ) [ ]j j n
d d
n
H e h n e 



 
1
[ ] ( )
2
j j n
d dh n H e e d

 


 
 

10. The impulse response will be

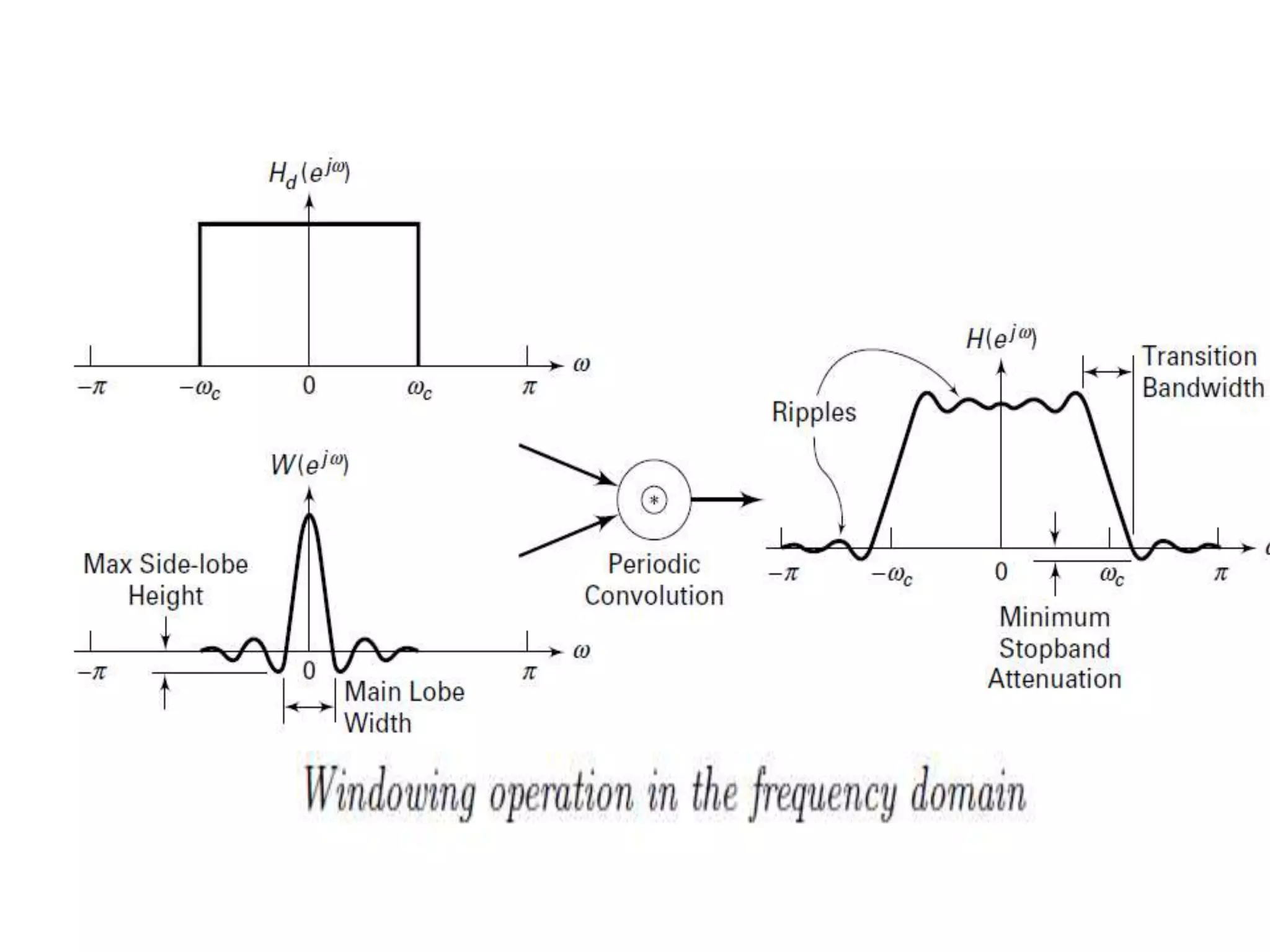
11. FIR Filter Design by Window function
technique
• To get this kind of systematic causal FIR to be
approximate, the most direct method
intercepts its ideal impulse response!
[ ] [ ] [ ]dh n w n h n
( ) ( ) ( )dH W H   

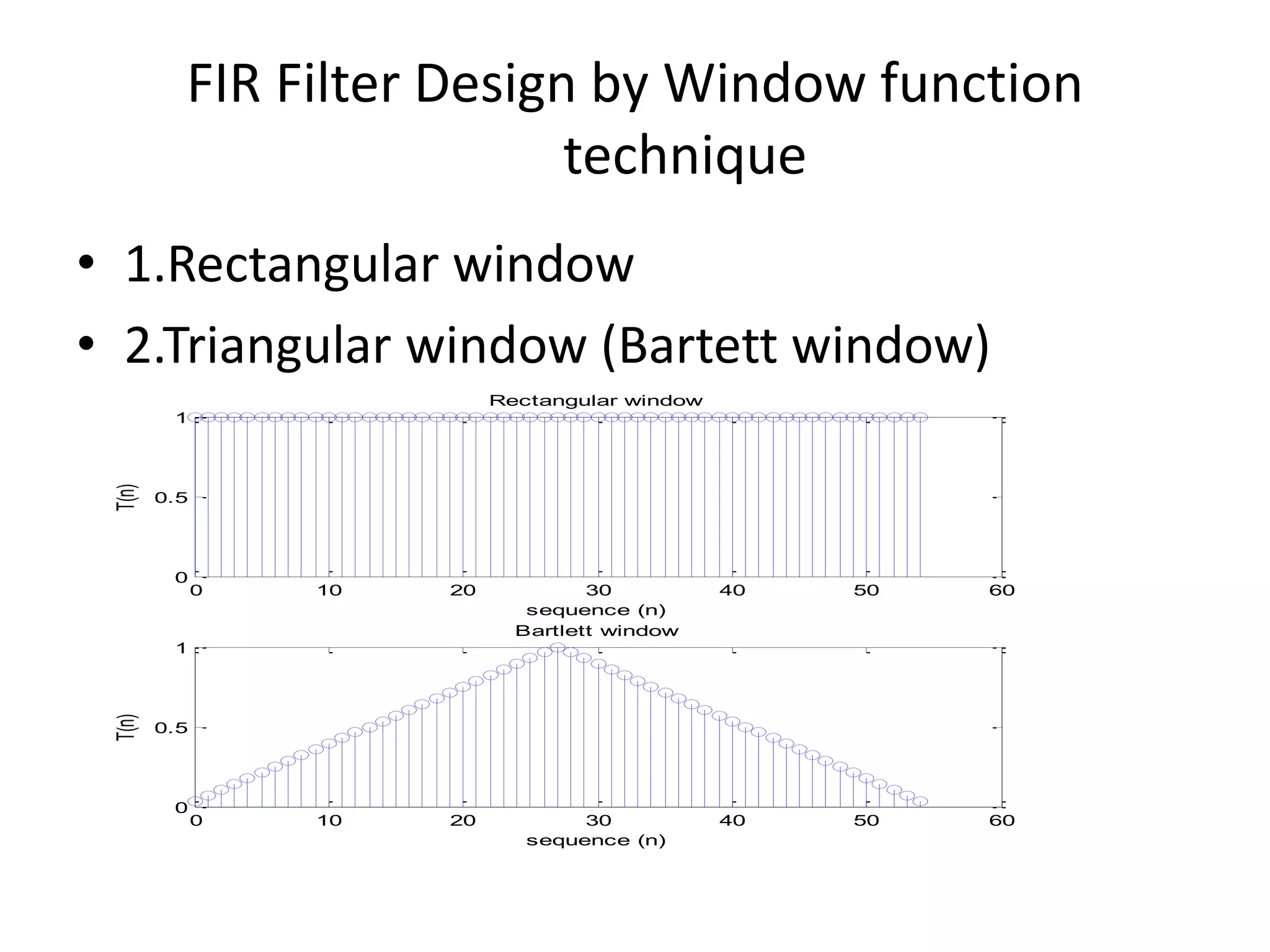
14. FIR Filter Design by Window function
technique
• 1.Rectangular window
• 2.Triangular window (Bartett window)
1, 0
[ ]
0,
n M
w n
otherwise
 
 

2 , 0
2
2[ ] 2 ,
2
0,
n Mn
M
n Mw n n M
M
otherwise
  


   



15. FIR Filter Design by Window function
technique
• 1.Rectangular window
• 2.Triangular window (Bartett window)
0 10 20 30 40 50 60
0
0.5
1
sequence (n)
T(n)
Rectangular window
0 10 20 30 40 50 60
0
0.5
1
sequence (n)
T(n)
Bartlett window

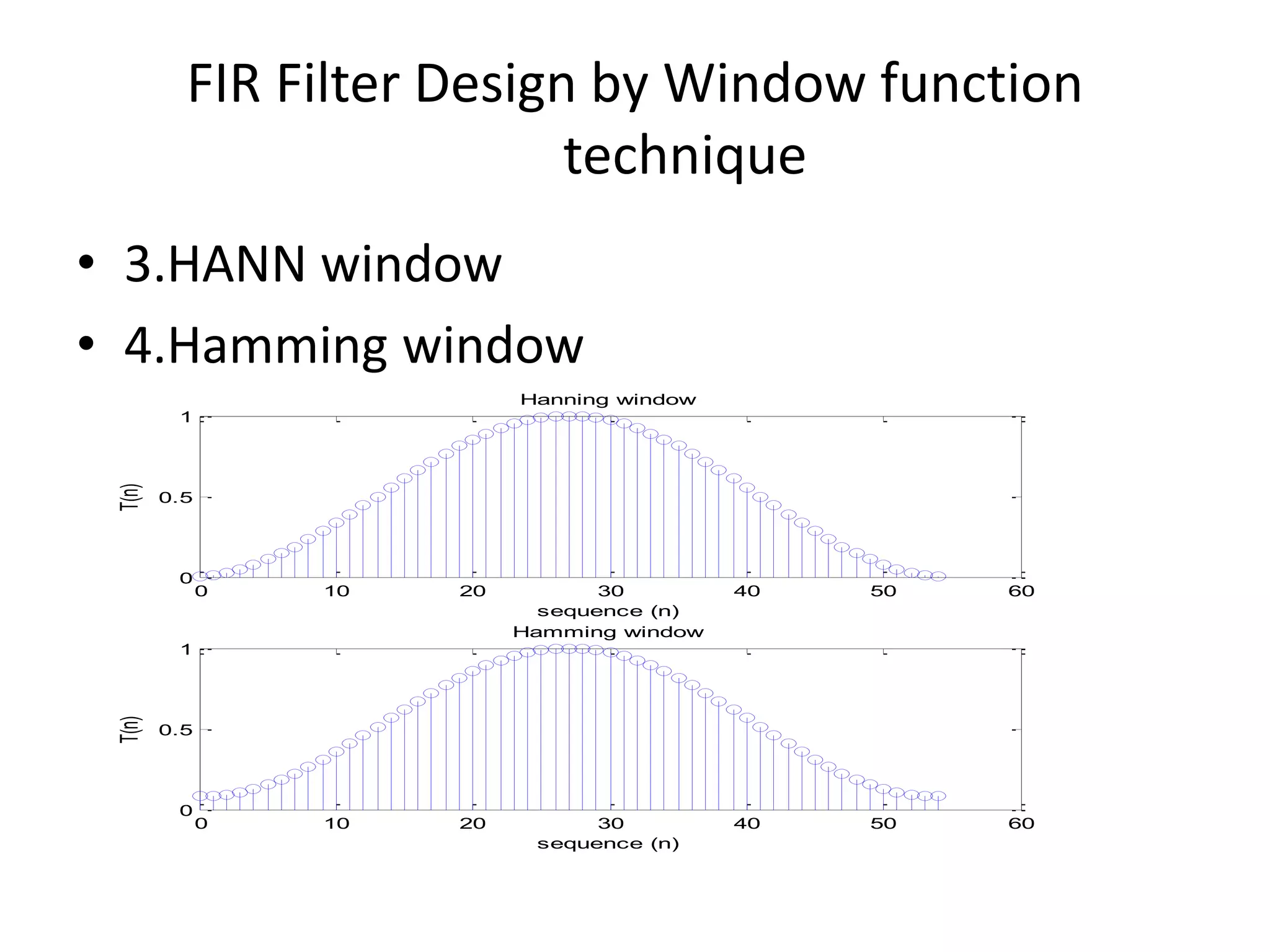
16. FIR Filter Design by Window function
technique
• 3.HANN window
• 4.Hamming window
1 2
1 cos , 0
[ ] 2
0,
n
n M
w n M
otherwise
  
      


2
0.54 0.46cos , 0
[ ]
0,
n
n M
w n M
otherwise

  
 


17. 0 10 20 30 40 50 60
0
0.5
1
sequence (n)
T(n)
Hanning window
0 10 20 30 40 50 60
0
0.5
1
sequence (n)
T(n)
Hamming window
FIR Filter Design by Window function
technique
• 3.HANN window
• 4.Hamming window

19. Frequency sampling-based FIR filter
design
• In this project we implemented FIR low and
high pass filters in matlab.
• For that we use matlab fir2 function that’s
uses frequency sampling to design filters.
• To obtain the filter coefficients, the function
applies an inverse fast Fourier transform to
the grid and multiplies by window.

20. • fir2(n,f,m) returns an nth-order FIR filter with
frequency-magnitude characteristics specified
in the vectors f and m. The function linearly
interpolates the desired frequency response
onto a dense grid and then uses the inverse
Fourier transform and a Hamming window to
obtain the filter coefficients.

21. Low pass Filter

23. Design a 30th-order low pass filter with a normalized cutoff
frequency of 0.6 PI rad/sample.

25. • Load the MAT-file chirp. The file contains a
signal, y, sampled at a frequency . y has most
of its power above , or half the Nyquist
frequency. Add random noise to the signal.
load chirp
y = y + 0.25*(rand(size(y))-0.5);

26. • Design a 34th-order FIR high pass filter. Specify a
cutoff frequency of 0.48. Visualize the frequency
response of the filter.

28. • It can be possible to implement this Hamming
window function for FIR filters to implement
low ,high,passband and stopband filters on
hardware (DSP Processor) for noise reduction
in any type of electonic circuits.