This document provides an overview of fault calculations, including:
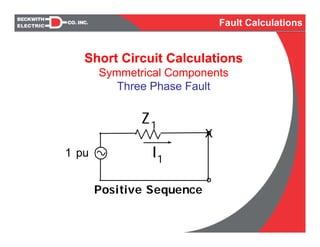
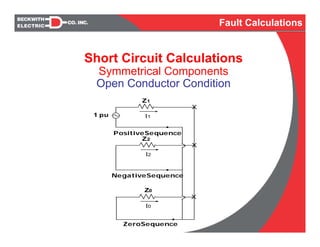
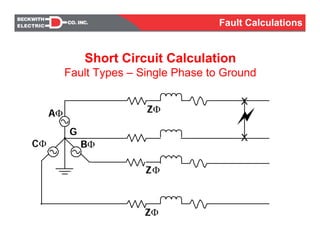
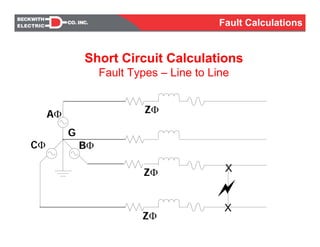
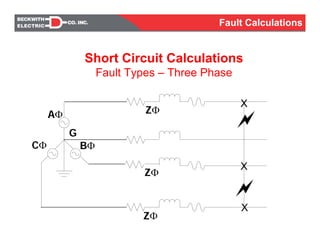
- Fault types such as single phase to ground, line to line, and three phase faults
- Calculation of symmetrical components using positive, negative, and zero sequence networks
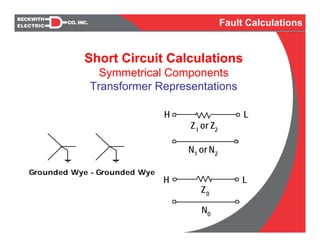
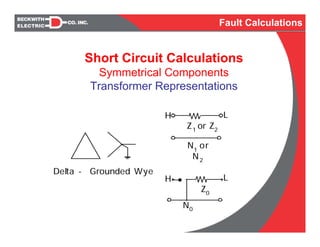
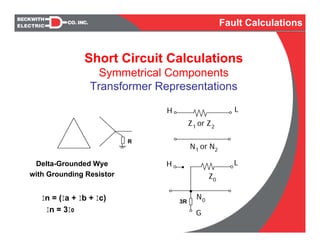
- Representation of system components like transformers using symmetrical components
- Examples of calculating fault currents for different fault scenarios using per-unit systems and symmetrical components
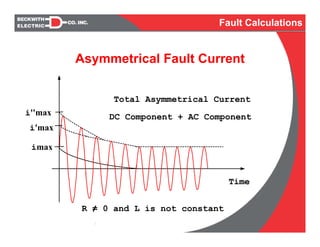
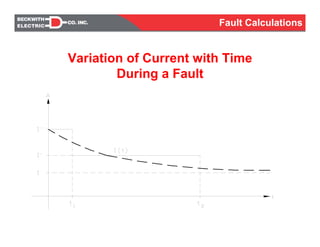
- Discussion of how fault currents vary over time and with transformer reactances


![Vmaxi(t) =
Z
[ sin(ωt + α – θ) – sin (α - θ)e – R t / L
]
Vm [ sin(ωt + α ) L
di
dt
] = + Ri
Vmax [sin(ωt + α )]
L R
Faulti(t)
sin (α - θ)e – R t / L
= Transient current
sin (ωt + α – θ) = Steady state current
Fault Calculations
Short Circuit Currents](https://image.slidesharecdn.com/fault-fundamentals-rev-080212-160117051103/85/Fault-Calculations-3-320.jpg)
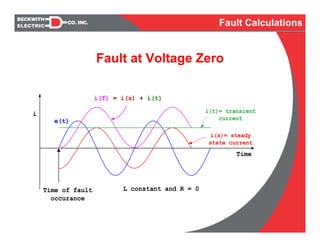
![Assume L is constant and R = 0
Time
e(t)
Time of fault
occurance
α
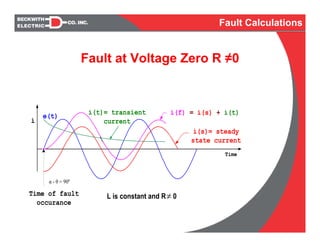
α - θ = 90º the fault occurs at V oltage zero:
[sin (ω t + α – θ) – sin (α - θ)]= sin (ω t + 90º) – sin (90º) = cos (ω t) -1
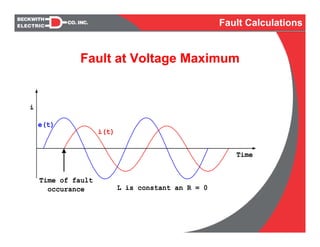
α = θ the fault occurs at V oltage m ax:
[sin (ω t + α – θ) – sin (α - θ)] = sin (ω t)
Vmax
I(t) = [ sin (ωt + α – θ) – sin (α - θ)]
Z
Vmax
I(t) = [ sin (ωt + α – θ) – sin (α - θ)e – R t / L
]
Z
Fault Inception Angle
Fault Calculations](https://image.slidesharecdn.com/fault-fundamentals-rev-080212-160117051103/85/Fault-Calculations-4-320.jpg)
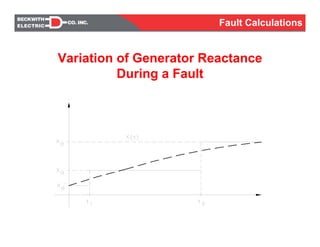
![Transient & Subtransient Reactance
Vmax [sin(ωt + α )]
jXd"
jXd'
jXd R
Faulti(t)
Fault Calculations](https://image.slidesharecdn.com/fault-fundamentals-rev-080212-160117051103/85/Fault-Calculations-8-320.jpg)

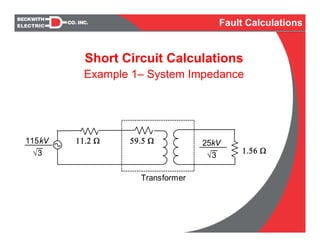

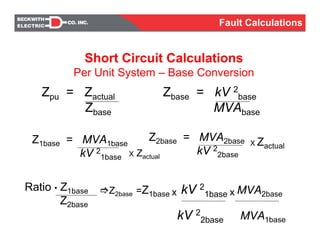
![Short Circuit Calculations
Example 1– Equivalent Impedance at 25 kV
√3
Z25 = Z115 x
[25/
115/√3
]2
0.53
2.80
11.2
59.5
25kV115 kV
System —
Xfrm —
Fault Calculations](https://image.slidesharecdn.com/fault-fundamentals-rev-080212-160117051103/85/Fault-Calculations-18-320.jpg)











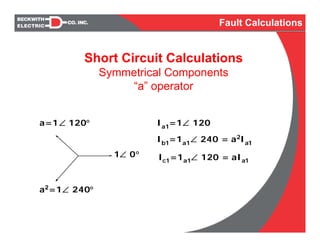
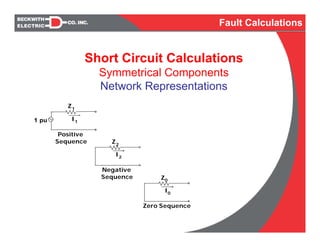
![Short Circuit Calculations
Symmetrical Components
Network Equations
Ia = I1+I2+I0 I1 = 1 [Ia+aIb+a2
Ic]
Ib = a2
I1+aI2+I0 I2 = 1 [Ia+a2
Ib+aIc]
Ic
= aI1
+a2I2
+I0
I0
= 1 [Ia
+Ib
+Ic
]
3
3
3
Fault Calculations](https://image.slidesharecdn.com/fault-fundamentals-rev-080212-160117051103/85/Fault-Calculations-32-320.jpg)
![Short Circuit Calculations
Symmetrical Component Vectors
I1=1/3 Ia
I2
= 1/3 [Ia
+a2Ib
+aIc
]
Ia
=1 ∠0
Ib=1∠ 240
Ic
=1∠ 120
I1
= 1/3 [Ia
+aIb
+a2Ic
]
aIb= 1∠ 120° 1∠ 240°x = 1 ∠ 360°
1∠ 240° 1 ∠ 120°x = 1∠ 360°a Ic=2
1∠ 240° 1 ∠ 240°x = 1∠ 120°a Ib
=2
aIc= 1∠ 120° 1∠ 120°x = 1 ∠ 240° I2 = 0
a2=1∠ 240°
∠ 120°a=1
Fault Calculations](https://image.slidesharecdn.com/fault-fundamentals-rev-080212-160117051103/85/Fault-Calculations-33-320.jpg)