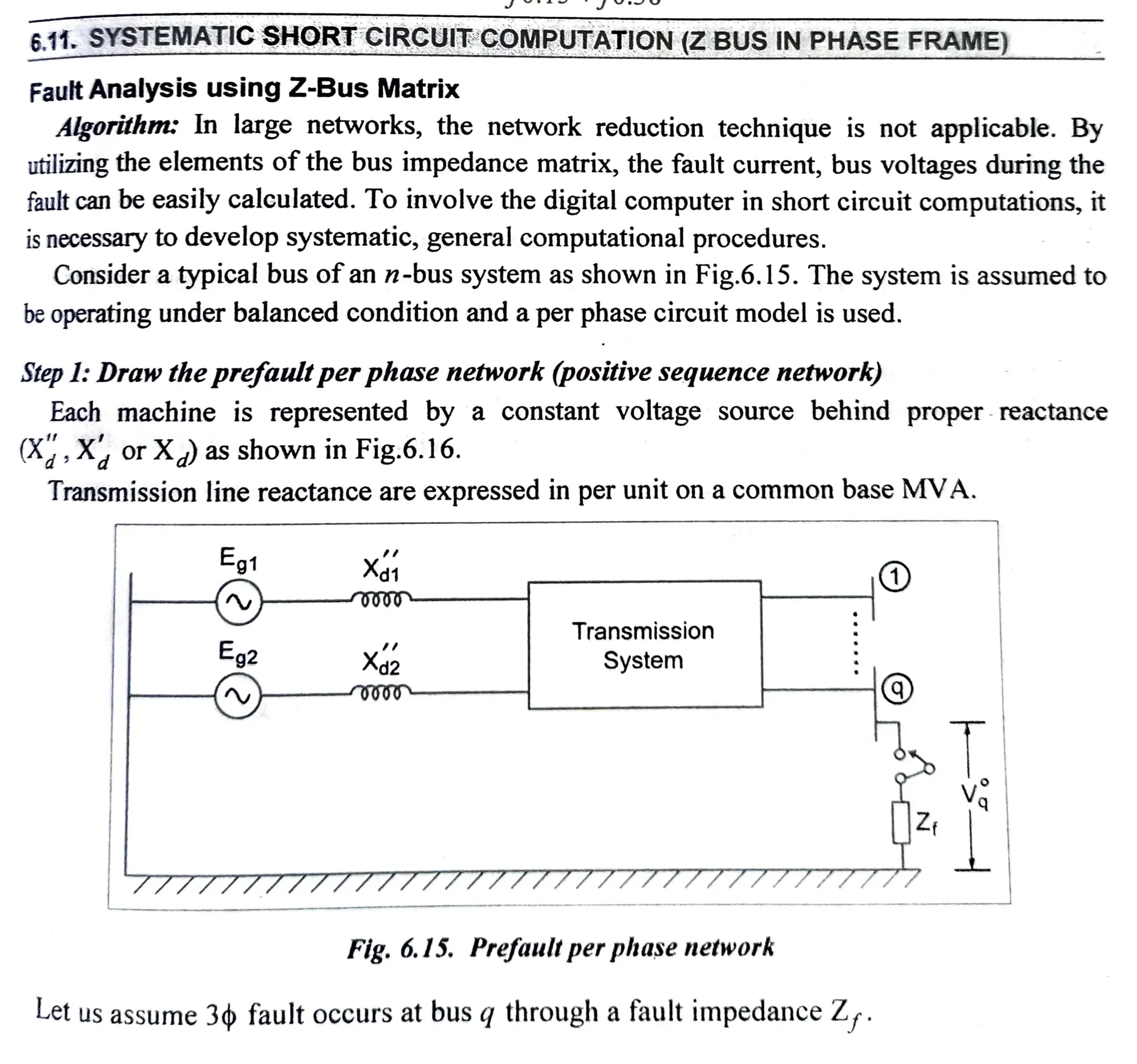
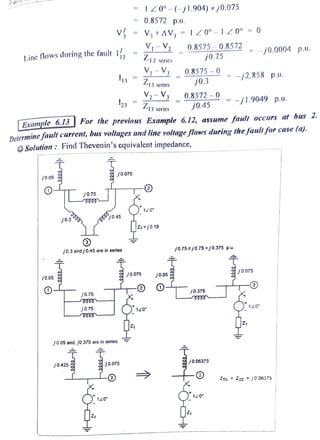
(1) A symmetrical fault occurs on bus 3 of a 3-bus system. (2) The Thevenin equivalent impedance is calculated to be j0.21 p.u. (3) For a fault impedance of j0.19 p.u., the fault current is calculated to be -j2.5 p.u. and the post-fault bus voltages are determined. (4) For a bolted fault with zero impedance, the fault current is -j4.76 p.u. and the post-fault bus voltages and line currents are found.

1. 6.11. SYSTEMATICSHORT CIRCUIT COMPUTATION(Z BUS IN PHASE FRAME)
Fautt Analysis using Z-Bus Matrix
Algorithm: In large networks, the network reduction technique is not applicable. By
utilizing the elements ofthe bus impedance matrix, the fault current, bus voltages during the
fault can be easily calculated. To involve the digital computer in short circuit computations, it
is necessary to develop systematic, general computational procedures.
Consider a typical bus ofan n-bus system as shown in Fig.6.15. The system is assumed to
be operating under balanced condition and a per phase circuit model is used.
Step1:Draw the prefault perphase network (positive sequence network)
Each machine is represented by a constant voltage source behind proper reactance
(X, X or X) as shown in Fig.6.16.
Transmission line reactance are expressed in per unit on a common base MVA.
Eg1
Eg2
Transmission
System
Fig. 6.15. Prefuultperphase network
Let us assume 3¢ fault occurs at bus q through a fault impedance Z,.

2. PrefaultBus Voltages
It is obtainedfrom the powerflowsolution.
Initial bus voltages,
prefault bus voltage i.e., Z, =
Agood approximationto representthe load by a constant impedance
evaluated at the
Step2: Obtain Zematrix usingbusbuildingalgorithm.
120°
bus
the Zous
Step 3: Obtain thefault current
From Fig.6.17,
v
120°
Fig. 6.16. Equivalentcircuit
Assume one node as reference node and short circuiting all the voltage sources. Determine
usingstepbystep bus buildingalgorithm.
Let us assume the prefault currents are negligible.
Zaa
Ztn
Faultçurrent
with allother sourcs
The changes in the network voltage caused by the added voltage V'
short circuited. By representing all components and loads by their appropriate impedancs
we obtain the Thevenin's circuit as shown inFig.6.17.
..
Z-Faultimpedance
Fig. 6.17. Thevenin's circuit
(614,
where Z is the diagonal element ofthe Zhus MatriN.

3. Step4: Obtain the Thevenin's network by insertingthe Thevenin's voltage source V" in
series with Z,and compute change in bus voltages using network equation.
Solving for AVbus
Thecurrent entering every bus is zero except at the faulted bus.
I, = ,...........= Iy=0 except I,
Change in bus voltage
'bus(F) Ybus A V
bus
AV,
AVs ZusIbus(
AV2
AV,
LAVE
bus
=
g s: Post fault Bus Voltages
*ein the bus voltages.
Fig. 6. 18. Thevenin 's network
:
Transmission :
systerm
bus
Zi1
LZN!
Vyus U) =V+AV,bus
(F)
Z12
ZN2
o
:
[Since the fault current is leaving the bus gl
ZiN
|2
ZN
0
-I,
0
(6.20)
Post fault bus voltages are obtained by superposition of the prefault bus voltages andthe
(Zbus=YaJ
.. (6.21)
(6.22)

4. EIEL:
v
v
In general,
Bus voltages during thefault
v - v
v
Fault current
V
v =
= 0
N
Step 6:Post FaultLine Currents
v -Z
If theshort circuit is solid or bolted (Z=0),
Post fault line current
- ZNg
Substitute fault current from cquation (6.19) inpost faultvoltage equation (6.24), we get,
+Z,
+Zf
=
Zijs
v-v
i#4
Lij series
ZN
i#4
()
Let us consider the line connecting between busesiand jwith series impedance Lis
(6.23)
...(6.24)
..(6.25)
... (6.26)
(6.27)
(6.28)
With the knowledge of the bus impedance matrix, the fault current and bus volage
during the fault and post fault line currents are obtained for any faulted bus. This method

5. ery simpleand practical. Thus all fault calculations are formulated in the bus frame of
cferenceusing busimpedance matrix Z
bus
Symmetrical Fault Analysis using Zhus(Flow chart)
Read the line data, bus data, fault bus, sub-transient reactances of each machine
Assume prefault load currents, shunt elements in transformer, transformer taps,
shunt capacitance, series resistance of lines are neglected.
Draw the prefault per phase network (positive sequence network)
obtain Zbus matrix using bus building algorithm
Start
Obtain prefault bus voltages from power flow solution
Draw the Thevenin's equivalent circuit and obtain the
fault current using
|AVN
If =
Compute change in bus voltages using network equation
[AV1 |Z1 Z12 - Z1q Z4N
v
Zog t Z
ZN1 ZN2 *" ZNg
VN
Compute change in bus voltages using network equation
= Vi-Ziq
v-Zgg
... ZgN
Zii series
... ZNN
Post fault line currents
End
-If
Print I. post fault voltages, post fault line currents, etc.

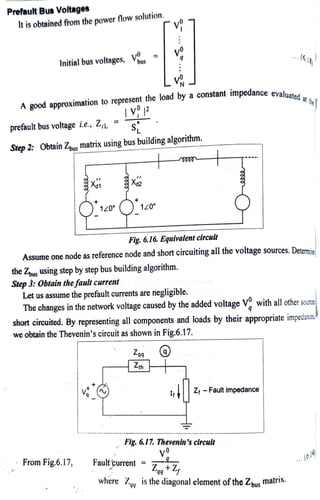
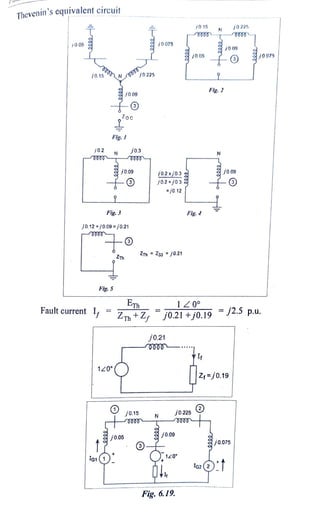
6. Example 6.10 A symmetrical fault occurs on bus 4 of system shown in Fig.
Determine the fuult current, postfault voltages and line crrents.
Lous
Zyus
Transformer : Xteak
G, G, : 100 MVA, 20KV, X* 15%
1
Ly, L, : Xt= 10%
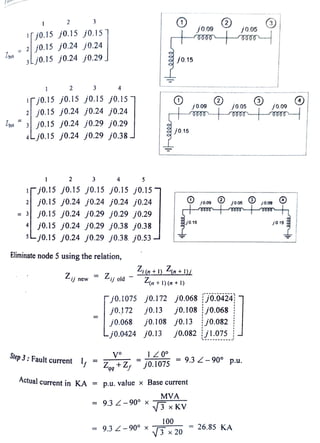
OSolution: Step l: Draw reactance diagram.
j0.15
= I[j0.15]
j0.09
120°
Step 2:Form Z-bus using bus building algorithm.
j0.15
2
9%
[j0.15 0.15
2Lj0.15 j0.24.
L
j0.09
Ly
j0.15
j0.1
j0.1
j0.05
3
j0.09
j0.09
-
1
j0.15
120°
4
j0.09
0000
j0.15
j0.15

7. Lyus
2
ifj0.15 j0.15 j0.1s1
= 2 j0.15 j0.24 j0.24
aLj0.15 j0.24 j0.29
3
j0.15 j0.15 j0.15 j0.15
2
3
2 j0.15 j0.24 j0.24 j0.24
3 j0.15 j0.24 j0.29 j0.29
aLj0.15 j0.24 j0.29 j0.38J
4
Zij
3
new
ICj0.15 j0.15 j0.15 j0.15 j0.15
4
2 j0.15 j0.24 j0.24 j0.24 j0.24
= 3 j0.15 j0.24 j0.29 j0.29 j0.29
4 j0.15 j0.24 j0.29 j0.38 j0.38
sLj0.15 j0.24 j0.29 j0.38. j0.53
Eliminate node 5using the relation,
Zij old
5
Step 3: Fault current Zog +Z
Zita +I) 2a+I)i
Zin +1)(n +1)
120°
j0.107s
j0.15
jo.15
= 9.3 Z-90° x
= 9.3L-90°x
Actual current in KA = p.U. value x Base current
j0.172 j0.13 j0.108 j0.068
j0.068 j0.108 j0. 13 j0.082
Lj0.0424 j0.13 j0.082 j1.075
100
rj0.1075 j0.172 j0.068 j0.0424}
j0.09
j0.09
MVA
V3 x KV
jo.09
V3 x20
2
2
2
= 9.3 Z-90°
j0.05
j0.05
jo.0s
p.u.
26.85 KA
(3)
j0.09
j0.09
jo.15

8. Step4: Postfault voltages
11 KV, 30 MVA
elements are :
j0.3 p.u.
v- Vo-Z,
V
Step 5: Post fault line currents.
Generator 1, Zp.u.
Transformer 1, Zpu.
=|/0°- j0.042 x 9.3 -90° = 0.6056 n.
= |20°- j0.082 x 9.3 Z-90° = 0.2374 nu
v = yo-Zy xl,
1Z0°-j0.068 x 9.3 Z-90°=0.3686
= |20°-j0.1075 x 9.3 Z-90° = 0 p.u.
new
new
=
= 2.634 p.u.
=
ijseries
V-v
Example 6.1|Generator G, and G, are identical and ratedas 11 KV, 30MVÀ nd
have a transient reactance of 0.3 p.u. at own MVAbase. The transformers T; and T, are
also identical and are rated 11/66 KV, 10 MVAand have a reactance of 0.075 per unit to
their own MVAbase. Then the line is 60 km long, each conductor has a reactance of
0.3686 -0.2374
j0.05
v-V
j0.075 p.u.
11/66 KV, 10 MVA
F
= j0.3
= 2.63 p.u.
0.2374-0
j0.09
j0.075 x
T2
Solution : Choose common base MVA as 30 MVA, then the reactance of various
= 2.637 p.u.
j0.075 p.u.
-(H-[0
0.6056 -0.3686
j0.09
66/11 KV, 10 MVA
11 KV, 30 MVA,
j0.3 p.u
= j0.3
= j0.225 p.u.
0.92 Okm. The 3 phasefault is assumed at point F, which is 25 km from generator G
Find the short circuit current.

9. Faulh
Transmissionline, Zpu.
Transforner 2, Zpu. new
Generator 2, Zpu.
Reactance diagram :
j0.3
j0.6834
Q000
XG1
120°
(0.92 x25) x
Example 6.12
=j0.3 x
F
= j0.075x
j0.225
Fault current I, =
Base current Ipase
Q000
Actual fault current in amperes is
j0.7468
120°
(
j0.1584
66)2
30 × 103
V3 x 66
66
6
XTL1
ETh 120°
XTh j0.3568
I, = 2.8023 - 90°
= |I||x Ihase
= 735.413 A
66 30
30
. Actual fault current = 2.8023 x 262.432
662
301|
j0.2218
XTL2
= 262.432 A
= j0.1584 p.u.
= j0.225 p.u.
= j0.3 p.u.
j0.225
j0.3568
= -j2.8023 p.u.
XG2 j03
)120°
If
Theone line diagram ofasimple three-bus system is as shown in Fig.
Each Benerator is represented by an emf behind the transient reactance. Allimpedances
are expressed in p.u. on acommon l00 MVA base, and
19 Determine the fault current, the bus voltages and the line currents during the fault
When a balanced three-phase fault with afault inpedance Z, =j0.19 per unit
OcCurs on bus 3.
new
new

10. j0.05
Z10
Zz0
(6) For bolted fault, detèrminefault current, bus voltages, lineflows.
OSolution : Case (a) : Find Thevenin equivalent impedance.
Zy0
Voltage source is Short circuited and the fault impedance open-circuited.
j0.05
j0.3
=
j0.76
j0.3
j=1
Converting A-connected network into Yconnected network using the formula,
j0.75
j0.225
jl.5
O.C
Z, xZi+1)
0.75 xj0.3
j0.75 +j0.45 +j0.3
j0.45
= j0.15
)/0.075
j0.75 xj0.45
j0.075
j0.75 +j0.45 +
10.3 *j0.225
=
j0.45 x j0.3
j0.75 +j0.45 +j0.3 j0.09

11. Thevenin's equivalent circuit
0 05
j0.16
j0.2
Fig. 5
Fig. i
Fig.3
1z0°
4
N
j0.12 +j0.09 =j0.21
Zoc
+
lo1()
j0.09
j0.09
ZTh
j0.05
j0225
j0.3
3
Fault current = Z tZ
Eth
j0.15
j0.075
j0.2 xj0.3
j0.2 +j03
ZTh = Za3 j0.21
=j0.12
j0.21
j0.225
j0.09
1Z0°
j0.21 +j0.19
140°
j015
Fig. 6.19.
j0 05
Fig. 4
A
Fig, 2
jo 09
j0225
j0.09
Z4-j0.19
= j2.5 p.u.
j0.075
j0075

12. Current contributed by generator I from Fig.6.19,
Ia
Bus voltages :
Current contributed by generator 2,
l2
Lineflows during thefautt :
V-V2
2 Li2 series
V,-V;
Z13 series
V,-V)
Bus voltage during the ault at bus I, v Vt t AV,
Z2 series
, x j0.2 +j0.3
Bus voltage during the fault at bus 2 =
= -I3
Bus voltage during the fault at bus 3 =
Erh
xj0.2 +j0.3
Fault current l ZTh
j0.3
j0.2
tbus 2 =
=
Current contributed by generator 2
Bus voltage during the fault at bus 1
Case (b) : For thebolted fault, Z,= 0
Current contributed by generator l =
=
j0.75
=
0.925 -0.925
=
=
j0.45
=
0.475 -0.925
=
V
-j2.5 xj0.3
j0.2 +j0.3
Vp.-G x
Z0
-j2.5 xj0.2
|20° (-jl.5xj0.05) = (0.925 p.u.
Vr t AV,
0.925 -0.4IS 15 p.u. = 1.5 2-90°
0.475
j0.3
j0.5
= 120°+j0.19(-j2.5) -1Z 0
= 0.475 p.u.
= -jl.0 =1.0 -90° p.u.
l20°- (-jl.0)xj0.075 = 0.925 p.u.
v = V,tAV,
120°
j0.21=-J4.76 p.u.
L, xj0.3
j0.2 +j0.3
=
= 0 p.u.
=-j1.5
L xj0.2
j0.2 +j0.3
2+j0.3
Vnr +AV,
=-jl.5 p.u.
=-jl.0 p.u.
=jl.0 p.u. = 1.0Z90° p.u.
= 0.8575 p.u.
-j2.857 p.u.
= p.u.
-jl.904
120° +
(G1Z)=1Z0°-(-j2.85) xj0.05
p.u.
V =V,t AV, = 1.0+(lGz xZzo)

13. Line flows during the fault 1, =
j0.05
j0.05
j0.3
j0.76
j0.425 &
j0.75
V= V, +AV, = |20°-I20° =
j0.75
j0.3 andj0.45 are in series
o045
j0.075
j0.05 and j0.375 are in series
12
120°
I20°-(-l.904) x/0.075
-0,8572 p.u.
j0.075
V,-V)
Example 6.13 For the previous Example 6.12, assume fault occurs at bus Z.
Determinefault current, bus voltages andline voltageflows during the faultforcase (4).
O
Solution: Find Thevenin's equivalent impedance,
j0.075
Z12 series
V- V,
Z13 series
Z13 series
120°
0.8575--0.8572
jo.05
j0.75
0.8575 -0
j0.3
0.8572 -0
j0.45
j0.375
j0.75 j0.75 =j0.375 p.u.
j0.06375
0
=-j2.858 p.u.
-j0.0004 p.u.
=-jl.9049 p.u.
j0.075
120
ZTh = Zz2 j0.06375

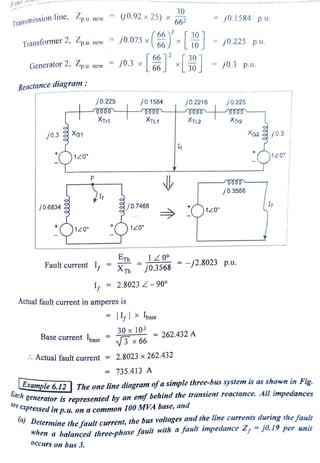
14. Faultcurrent I,
Current contribution by generators:
Bus voltages & Line flows :
From Fig.1,
V
Current contribution by generator 1, lG =
=
I3 =
V.
10°
j0.06375 +
j0.19
jO.05 +j0.375]
Current contributed by generator 2, IG2 = (-j3.94) x j0.05 +j0.375 +j0.075
L3=
j0 05
VË-V2
j0.375
= Vpt t AV, = 120°-lGË xZi0
Z=j1,9|I
Z12 series
= 120° -(-j0.591) xj0.05 = 0.97 p.u.
V;-V,
-j3.94 p.u.
Z3 serics
2
p.rtAV = l20°- I XZn
I,xj0.075
j0.05 +j0.375 +j0.075
-j3.94xj0.03 - -j0.591 p.u.
=
j0.5
= -j3.349 p.u.
= |20°-(-j3.349) xj0.075 = 0.7488 p.u.
0.97-0.7488
j0.75
lG-I2 = -j0.591 -(-j0.295) = -j0.296 p.u.
Vi3 = I3x Z13 series =-j0.296 xj0.3 = 0.089 p.u.
j0075
0.7488-0.881
j0.45
v{ = V-Vi3 = 0.97-0.089 = 0.881 p.u.
-j0.295 p.u.
= j0.294 p.u.