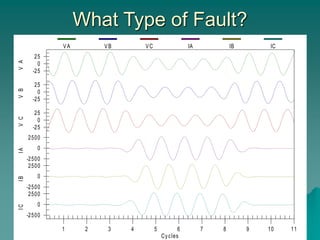
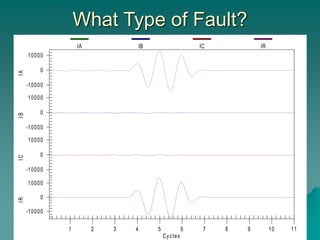
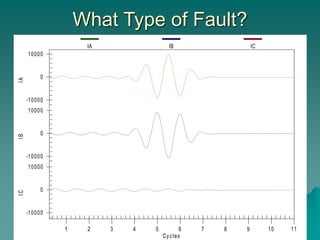
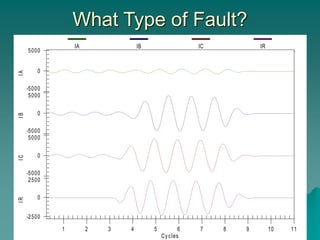
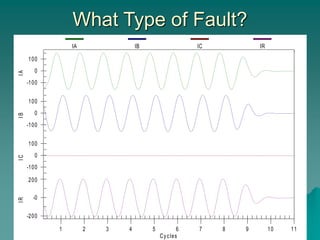
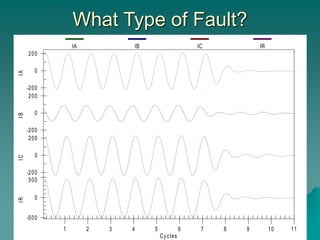
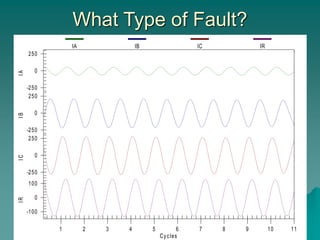
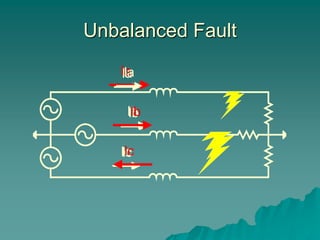
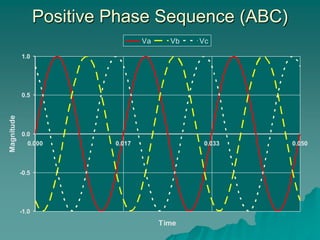
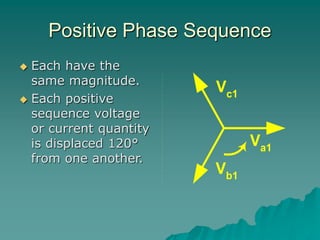
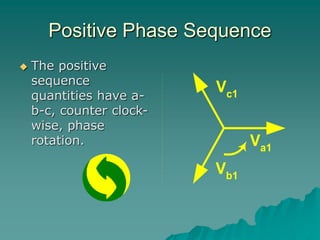
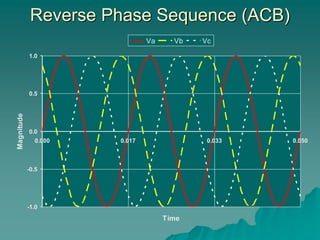
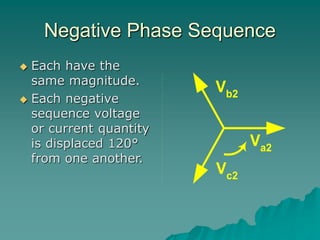
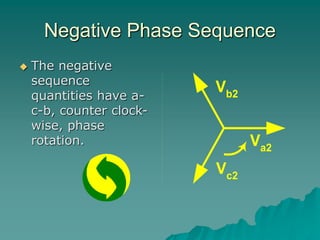
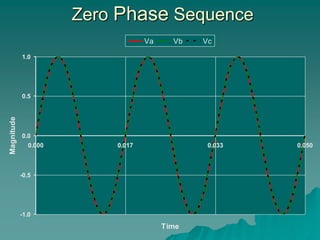
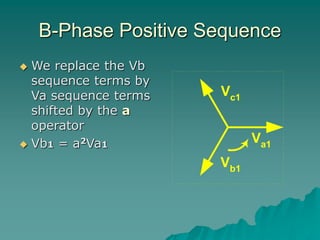
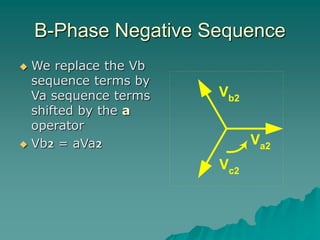
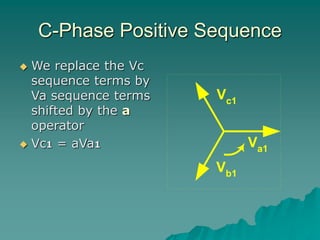
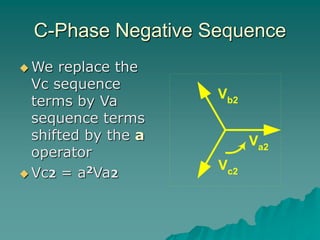
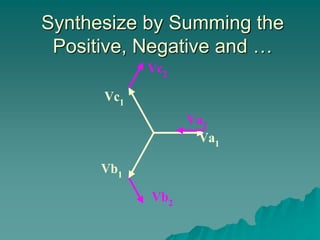
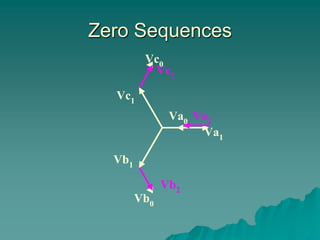
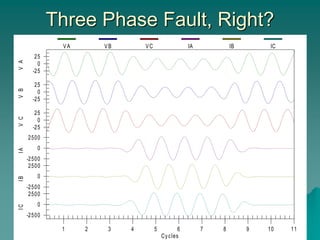
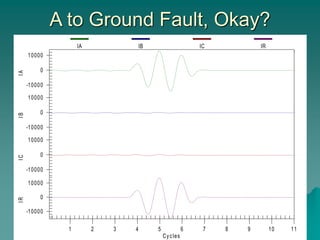
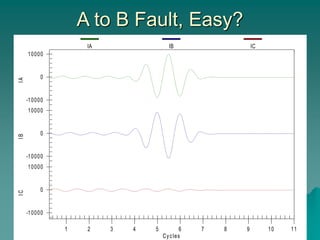
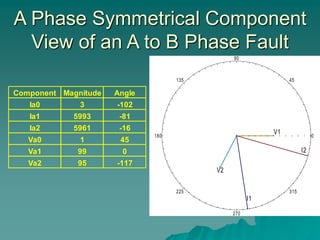
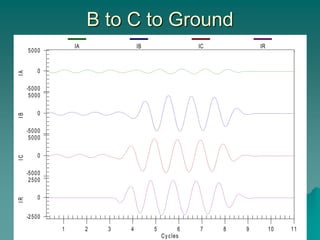
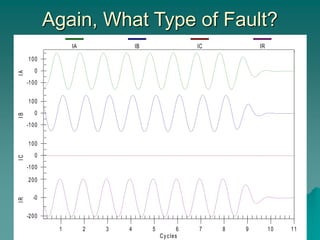
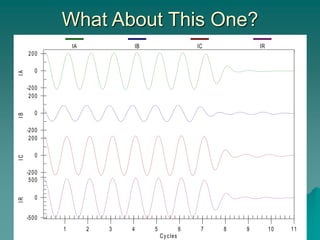
This document provides an introduction to symmetrical components analysis for power system fault analysis. It discusses key symmetrical component concepts including positive, negative, and zero sequence components. Equations are presented for transforming unbalanced three-phase systems into balanced symmetrical components as well as for analyzing and synthesizing systems from the component quantities. Various fault types are reviewed including three-phase, phase-to-phase, phase-to-ground, open phase, and examples are shown of interpreting faults using symmetrical components.

1. Symmetrical Components I
An Introduction to Power System Fault
Analysis Using Symmetrical Components
Dave Angell
Idaho Power
21st Annual
Hands-On Relay School

2. What Type of Fault?
-25
0
25
-25
0
25
-25
0
25
-2500
0
2500
-2500
0
2500
-2500
0
2500
1 2 3 4 5 6 7 8 9 10 11
V
A
V
B
V
C
I
A
I
B
I
C
Cycles
VA VB VC IA IB IC

3. What Type of Fault?
-10000
0
10000
-10000
0
10000
-10000
0
10000
-10000
0
10000
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

4. What Type of Fault?
-10000
0
10000
-10000
0
10000
-10000
0
10000
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
Cycles
IA IB IC

5. What Type of Fault?
-5000
0
5000
-5000
0
5000
-5000
0
5000
-2500
0
2500
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

6. What Type of Fault?
-100
0
100
-100
0
100
-100
0
100
-200
-0
200
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

7. What Type of Fault?
-200
0
200
-200
0
200
-200
0
200
-500
0
500
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

8. What Type of Fault?
-250
0
250
-250
0
250
-250
0
250
-100
0
100
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

9. Basic Course Topics
 Terminology
 Phasors
 Equations
 Fault Analysis Examples
 Calculations

10. Unbalanced Fault
Ia
Ib
Ic
Ia
Ib
Ic
Ia
Ib
Ic

11. Symmetrical Component
Phasors
 The unbalanced three phase system
can be transformed into three
balanced phasors.
– Positive Sequence
– Negative Sequence
– Zero Sequence

12. Positive Phase Sequence (ABC)
-1.0
-0.5
0.0
0.5
1.0
0.000 0.017 0.033 0.050
Time
Magnitude
Va Vb Vc

13. Positive Phase Sequence
 Each have the
same magnitude.
 Each positive
sequence voltage
or current quantity
is displaced 120°
from one another.
Va1
Vb1
Vc1

14. Positive Phase Sequence
 The positive
sequence
quantities have a-
b-c, counter clock-
wise, phase
rotation. Va1
Vb1
Vc1

15. Reverse Phase Sequence (ACB)
-1.0
-0.5
0.0
0.5
1.0
0.000 0.017 0.033 0.050
Time
Magnitude
Va Vb Vc

16. Negative Phase Sequence
 Each have the
same magnitude.
 Each negative
sequence voltage
or current quantity
is displaced 120°
from one another.
Va2
Vc2
Vb2

17. Negative Phase Sequence
 The negative
sequence
quantities have a-
c-b, counter clock-
wise, phase
rotation. Va2
Vc2
Vb2

18. Zero Phase Sequence
-1.0
-0.5
0.0
0.5
1.0
0.000 0.017 0.033 0.050
Time
Magnitude
Va Vb Vc

19. Zero Phase Sequence
 Each zero
sequence quantity
has the same
magnitude.
 All three phasors
with no angular
displacement
between them, all
in phase.
Va0
Vb0
Vc0

20. Symmetrical Components
Equations
 Each phase quantity is equal to the
sum of its symmetrical phasors.
 Va = Va0 + Va1 +Va2
 Vb = Vb0 + Vb1 +Vb2
 Vc = Vc0 + Vc1 +Vc2
 The common form of the equations
are written in a-phase terms.

21. The a Operator
 Used to shift the a-phase terms to
coincide with the b and c-phase
 Shorthand to indicate 120° rotation.
 Similar to the j operator of 90°.
Va

22. Rotation of the a Operator
 120° counter clock-wise rotation.
 A vector multiplied by 1 /120° results in
the same magnitude rotated 120°.
Va
aVa

23. Rotation of the a2 Operator
 240° counter clock-wise rotation.
 A vector multiplied by 1 /240° results in
the same magnitude rotated 240°.
Va
a2Va

24. B-Phase Zero Sequence
 We replace the
Vb sequence
terms by Va
sequence terms
shifted by the a
operator.
 Vb0 = Va0
Va0
Vb0
Vc0

25. B-Phase Positive Sequence
 We replace the Vb
sequence terms by
Va sequence terms
shifted by the a
operator
 Vb1 = a2Va1
Va1
Vb1
Vc1

26. B-Phase Negative Sequence
 We replace the Vb
sequence terms by
Va sequence terms
shifted by the a
operator
 Vb2 = aVa2 Va2
Vc2
Vb2

27. C-Phase Zero Sequence
 We replace the
Vc sequence
terms by Va
sequence terms
shifted by the a
operator.
 Vc0 = Va0
Va0
Vb0
Vc0

28. C-Phase Positive Sequence
 We replace the Vc
sequence terms by
Va sequence terms
shifted by the a
operator
 Vc1 = aVa1 Va1
Vb1
Vc1

29. C-Phase Negative Sequence
 We replace the
Vc sequence
terms by Va
sequence terms
shifted by the a
operator
 Vc2 = a2Va2
Va2
Vc2
Vb2

30. What have we produced?
 Va = Va0 + Va1 + Va2
 Vb = Va0 + a2Va1 + aVa2
 Vc = Va0 + aVa1 + a2Va2

31. Symmetrical Components
Equations
 Analysis
– To find out of the amount of the
components
 Synthesis
– The combining of the component
elements into a single, unified entity

32. Symmetrical Components
Synthesis Equations
 Va = Va0 + Va1 + Va2
 Vb = Va0 + a2Va1 + aVa2
 Vc = Va0 + aVa1 + a2Va2

33. Symmetrical Components
Analysis Equations
 Va0 = 1/3 ( Va + Vb + Vc)
 Va1= 1/3 (Va + aVb + a2Vc)
 Va2= 1/3 (Va + a2Vb + aVc)

34. Symmetrical Components
Analysis Equations - 1/3 ??
 Where does the 1/3 come from?
 Va1= 1/3 (Va + aVb + a2Vc)
 Va = Va0 + Va1 + Va2
 When balanced
0 0

35. Symmetrical Components
Analysis Equations - 1/3 ??
 Va1= 1/3 (Va + aVb + a2Vc)
 Adding the phases
Va

36. Symmetrical Components
Analysis Equations - 1/3 ??
 Va1= 1/3 (Va + aVb +
a2Vc)
 Adding the phases yields
Va
aVb
Vc
Va
Vb

37. Symmetrical Components
Analysis Equations - 1/3 ??
 Va1= 1/3 (Va + aVb +
a2Vc)
 Adding the phases yields
3 Va.
 Divide by the 3 and now
Va = Va1
a2
Vc
Va
aVb
Vc
Va
Vb

38. Example Vectors
An Unbalanced Voltage
Va
Vc
Vb
 Va = 13.4 /0°
 Vb = 59.6 /-
104°
 Vc = 59.6 /104°

39. Analysis Results in These
Sequence Quantities
Va0
Vb0
Vc0
Va2
Vc2
Vb2
Va1
Vb1
Vc1
 Va0 = -5.4 s Va1 = 42.9 s Va2 = -24.1

40. Synthesize by Summing the
Positive, Negative and …
Va2
Vb2
Vc2
Va1
Vb1
Vc1

41. Zero Sequences
Va2
Vb2
Vc2
Va0
Vb0
Vc0
Va1
Vb1
Vc1

42. The Synthesis Equation Results
in the Original Unbalanced
Voltage
Va2
Vb2
Vc2
Va0
Vb0
Vc0
Va1
Vb1
Vc1
Va
Vc
Vb

43. Symmetrical Components
Present During Shunt Faults
 Three phase fault
– Positive
 Phase to phase
fault
– Positive
– Negative
 Phase to
ground fault
– Positive
– Negative
– Zero

44. Symmetrical Component
Review of Faults Types
 Let’s return to the example fault
reports and view the sequence
quantities present

45. Three Phase Fault, Right?
-25
0
25
-25
0
25
-25
0
25
-2500
0
2500
-2500
0
2500
-2500
0
2500
1 2 3 4 5 6 7 8 9 10 11
V
A
V
B
V
C
I
A
I
B
I
C
Cycles
VA VB VC IA IB IC

46. A Symmetrical Component View
of an Three-Phase Fault
Component Magnitude Angle
Ia0 7.6 175
Ia1 2790 -64
Ia2 110 75.8
Va0 0 0
Va1 18.8 0
Va2 0.7 337
0
45
90
135
180
225
270
315
I1
V1

47. A to Ground Fault, Okay?
-10000
0
10000
-10000
0
10000
-10000
0
10000
-10000
0
10000
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

48. A Symmetrical Component View
of an A-Phase to Ground Fault
Component Magnitude Angle
Ia0 7340 -79
Ia1 6447 -79
Ia2 6539 -79
Va0 46 204
Va1 123 0
Va2 79 178
0
45
90
135
180
225
270
315
I0
I1
I2
V0 V1
V2

49. Single Line to Ground Fault
 Voltage
– Negative and zero sequence 180 out of
phase with positive sequence
 Current
– All sequence are in phase

50. A to B Fault, Easy?
-10000
0
10000
-10000
0
10000
-10000
0
10000
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
Cycles
IA IB IC

51. A Phase Symmetrical Component
View of an A to B Phase Fault
Component Magnitude Angle
Ia0 3 -102
Ia1 5993 -81
Ia2 5961 -16
Va0 1 45
Va1 99 0
Va2 95 -117
0
45
90
135
180
225
270
315
I1
I2
V1
V2

52. C Phase Symmetrical Component
View of an A to B Phase Fault
Component Magnitude Angle
Ic0 3 138
Ic1 5993 279
Ic2 5961 104
Vc0 1 -75
Vc1 99 0
Vc2 95 2.5
0
45
90
135
180
225
270
315
I1
I2
V1
V2

53. Line to Line Fault
 Voltage
– Negative in phase with positive
sequence
 Current
– Negative sequence 180 out of phase
with positive sequence

54. B to C to Ground
-5000
0
5000
-5000
0
5000
-5000
0
5000
-2500
0
2500
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

55. A Symmetrical Component View
of a B to C to Ground Fault
Component Magnitude Angle
Ia0 748 97
Ia1 2925 -75
Ia2 1754 101
Va0 8 351
Va1 101 0
Va2 18 348
0
45
90
135
180
225
270
315
I0
I1
I2
V0
V1
V2

56. Line to Line to Ground Fault
 Voltage
– Negative and zero in phase with positive
sequence
 Current
– Negative and zero sequence 180 out of
phase with positive sequence

57. Again, What Type of Fault?
-100
0
100
-100
0
100
-100
0
100
-200
-0
200
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

58. C Symmetrical Component View
of a C-Phase Open Fault
Component Magnitude Angle
Ic0 69 184
Ic1 101 4
Ic2 32 183
Vc0 0 162
Vc1 79 0
Vc2 5 90
0
45
90
135
180
225
270
315
I0
I1
I2
V1
V2

59. One Phase Open (Series)
Faults
 Voltage
– No zero sequence voltage
– Negative 90 out of phase with positive
sequence
 Current
– Negative and zero sequence 180 out of
phase with positive sequence

60. What About This One?
-200
0
200
-200
0
200
-200
0
200
-500
0
500
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

61. Ground Fault with Reverse Load
Ic0 164 -22
Ic1 89 -113
Ic2 41 -6
Vc0 4 -123
Vc1 38 0
Vc2 6 -130
0
45
90
135
180
225
270
315
I0
I1
I2
V0
V1
V2

62. Finally, The Last One!
-250
0
250
-250
0
250
-250
0
250
-100
0
100
1 2 3 4 5 6 7 8 9 10 11
I
A
I
B
I
C
I
R
Cycles
IA IB IC IR

63. Component Magnitude Angle
Ic0 45 40
Ic1 153 -4
Ic2 132 180
Vc0 0.5 331
Vc1 40 0
Vc2 0.5 93
Fault on Distribution System
with Delta – Wye Transformer
0
45
90
135
180
225
270
315
I0
I1
I2
V0
V1
V2

64. Use of Sequence Quantities in
Relays
 Zero Sequence filters
– Current
– Voltage
 Relay operating quantity
 Relay polarizing quantity

65. Zero Sequence Current
Ia
Ib
Ic
Direction of the
protected line
Ia+Ib+Ic
3I0

66. Zero Sequence Voltage
(Broken Delta)
Va
Vb
Vc
3V0

67. Zero Sequence Voltage
Va
Va
Vc
Vb
Va
Vb
3Vo
Va
Vb

68. Sequence Operating Quantities
 Zero and negative sequence currents
are not present during balanced
conditions.
 Good indicators of unbalanced faults

69. Sequence Polarizing Quantities
 Polarizing quantities are used to
determine direction.
 The quantities used must provide a
consistent phase relationship.

70. Zero Sequence Voltage
Polarizing
 3Vo is out of phase with Va
 -3Vo is used to polarize for ground faults
Va
Vb
3Vo

71. Learning Check
 Given three current sources
 How can zero sequence be produced
to test a relay?
 How can negative sequence
produced?

72. How can zero sequence be
produced to test a relay?
 A single source provides positive,
negative and zero sequence
– Note that each sequence quantity will
be 1/3 of the total current
 Connect the three sources in parallel
and set their amplitude and the
phase angle equal to one another
– The sequence quantities will be equal to
each source output

73. How can negative sequence
produced?
 A single source provides positive, negative
and zero sequence
– Each sequence quantity will be 1/3 of the total
current
 Set the three source’s amplitude equal to
one another and the phase angles to
produce a reverse phase sequence (Ia at
/0o
, Ib at /120o
and Ic at /-120o
)
– Only negative sequence will be produced

74. Advanced Course Topics
 Sequence Networks
 Connection of Networks for Faults
 Per Unit System
 Power System Element Models

75. References
 Symmetrical Components for Power
Systems Engineering, J Lewis
Blackburn
 Protective Relaying, J Lewis Blackburn
 Power System Analysis, Stevenson
 Analysis of Faulted Power System, Paul
Anderson

76. Conclusion
 Symmetrical components provide:
– balanced analysis of an unbalanced
system.
– a measure of system unbalance
– methods to detect faults
– an ability to distinguish fault direction